Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để Olm.vn giúp em nhé
Tính:
A = \(\dfrac{7}{2}\) + \(\dfrac{7}{4}\) + \(\dfrac{7}{8}\) + \(\dfrac{7}{16}\)+...+ \(\dfrac{7}{256}\)
A = \(\dfrac{7}{2}\) + \(\dfrac{7}{4}\) + \(\dfrac{7}{8}\) + \(\dfrac{7}{16}\) +...+ \(\dfrac{7}{128}\)+ \(\dfrac{7}{256}\)
A\(\times\) 2 = 7 + \(\dfrac{7}{2}\) + \(\dfrac{7}{4}\) + \(\dfrac{7}{8}\)+ \(\dfrac{7}{16}\)+...+ \(\dfrac{7}{128}\)
A \(\times\) 2 - A = 7 - \(\dfrac{7}{256}\)
A \(\times\) (2-1) = \(\dfrac{1785}{256}\)
A = \(\dfrac{1785}{256}\)
A =\(\dfrac{7}{2}\)+\(\dfrac{7}{4}\)+\(\dfrac{7}{8}\)+...+\(\dfrac{7}{256}\)
A*2 =7+\(\dfrac{7}{2}\)+\(\dfrac{7}{4}\)+...+\(\dfrac{7}{256}\)
A*2-A=7-\(\dfrac{7}{256}\)
A=\(\dfrac{\text{1785 }}{256}\)

Gọi P là 1 giá trị của biểu thức trên.
Ta có \(P=\dfrac{ax+b}{x^2+1}\Leftrightarrow\left(x^2+1\right)P-\left(ax+b\right)=0\)
\(\Leftrightarrow Px^2-ax+P-b=0\left(1\right)\)
Vì giá trị nhỏ nhất và giá trị lớn nhất đều khác 0, nên \(P\ne0\)
Để P tồn tại thì phương trình (1) phải có nghiệm hay \(\Delta_{\left(1\right)}\ge0\)
\(\Leftrightarrow\left(-a\right)^2-4P\left(P-b\right)\ge0\Leftrightarrow4P^2-4Pb-a^2\le0\left(2\right)\)
Gọi \(P_1,P_2\left(P_1< P_2\right)\) là 2 nghiệm của phương trình \(4P^2-4Pb-a^2=0\left(3\right)\)
Khi đó phương trình (2) có nghiệm \(P_1\le P\le P_2\) nên P đạt Min tại giá trị \(P_1\), đạt Max tại giá trị \(P_2\).
Do đó, yêu cầu của bài toán chỉ thỏa mãn khi và chỉ khi phương trình (3) có 2 nghiệm -1 và 4, tức: \(\left\{{}\begin{matrix}4+4b-a^2=0\\64-16b-a^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=3\\a^2=16\end{matrix}\right.\) hay \(\left\{{}\begin{matrix}b=3\\a=\pm4\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}a=4\\b=3\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}a=-4\\b=3\end{matrix}\right.\)

So sánh phân số bằng cách quy đồng mẫu số
\(\dfrac{6}{17}\) < \(\dfrac{x}{22}\) < \(\dfrac{7}{17}\)
\(\dfrac{6\times22}{17\times22}\) < \(\dfrac{x\times17}{22\times17}\)< \(\dfrac{7\times22}{17\times22}\)
132 < \(x\times\) 17 < 154
132 : 17 < \(x\) < 154 : 17
\(\dfrac{132}{17}\) < \(x\) < \(\dfrac{154}{17}\)
7,76 < \(x\) < 9,05
Vì \(x\) là số tự nhiên nên \(x\) = 8
Vậy số cần điền vào chỗ trống là 8
Đáp số: 8

Khi bớt ở cả hai số đi cùng một số đơn vị thì hiệu hai số không đổi và bằng:
94 - 78 = 16
Theo bài ra ta có sơ đồ: 
Theo sơ đồ ta có:
Số bé lúc sau là: 16: (5 - 4) \(\times\) 4 = 64
Số k cần bớt ở cả hai số là: 78 - 64 = 14
Đáp số: 14
Lời giải:
Theo bài ra ta có:
$\frac{78-k}{94-k}=\frac{4}{5}$
Suy ra $5\times (78-k)=4\times (94-k)$
$5\times 78-5\times k =4\times 94-4\times k$
$390-5\times k = 376-4\times k$
$390-376=5\times k -4\times k$
$14=k\times (5-4)$
$14=k$






đây nhé bạn cầm tạm mình ko cho file vào đc!!!
nếu bạn thích thì cho mình xin 1 tick nhé!!❤

Hiệu số phần bằng nhau:
5-4=1(phần)
Hiệu của mẫu và tử khi cộng thêm m vào mỗi bên:
171 - 132= 39
Phân số mới có mẫu số là:
39:1 x 5= 195 ɪə
Số tự nhiên m cần tìm là:
195 - 132= 63

Tổng số tuổi hai chị em Quyên hiện nay:
44:2=22(tuổi)
Số năm nữa tới khi mẹ 54 tuổi:
54-44=10(năm)
Khi mẹ 54 tuổi, tổng tuổi 2 chị em Quyên là:
10 x 2 + 22 = 42 (tuổi)
Khi mẹ 54 tuổi thì Quyên:
(42-6):2=18(tuổi)
Khi mẹ 54 tuổi thì chị của Quyên:
(42+6):2=24(tuổi)


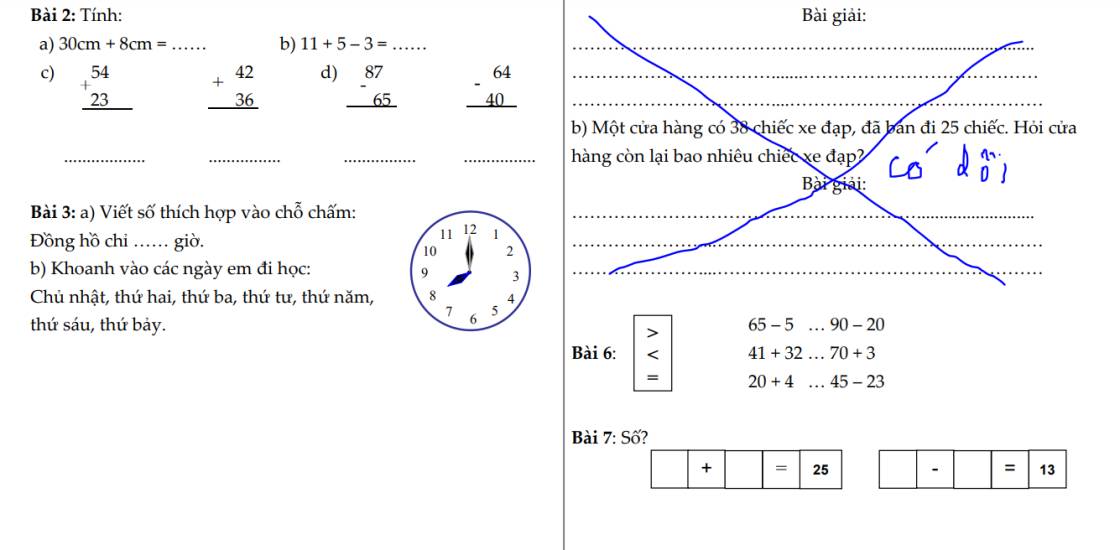

Lời giải:
Đặt $x-y=a; y-z=b, z-x=c$
$\Rightarrow a+b+c=0$
Theo đề ta có:
$(x-y)^2+(y-z)^2+(z-x)^2=[(z-x)-(x-y)]^2+[(x-y)-(y-z)]^2+[(y-z)-(z-x)]^2$
$\Leftrightarrow a^2+b^2+c^2=(c-a)^2+(a-b)^2+(b-c)^2$
$\Leftrightarrow a^2+b^2+c^2=2a^2+2b^2+2c^2-2(ab+bc+ac)$
$\Leftrightarrow 2(a^2+b^2+c^2)=a^2+b^2+c^2+2(ab+bc+ac)$
$\Leftrightarrow 2(a^2+b^2+c^2)=(a+b+c)^2=0$
$\Rightarrow a^2+b^2+c^2=0$
$\Rightarrow a=b=c=0$
$\Leftrightarrow x-y=y-z=z-x=0$
$\Leftrightarrow x=y=z$