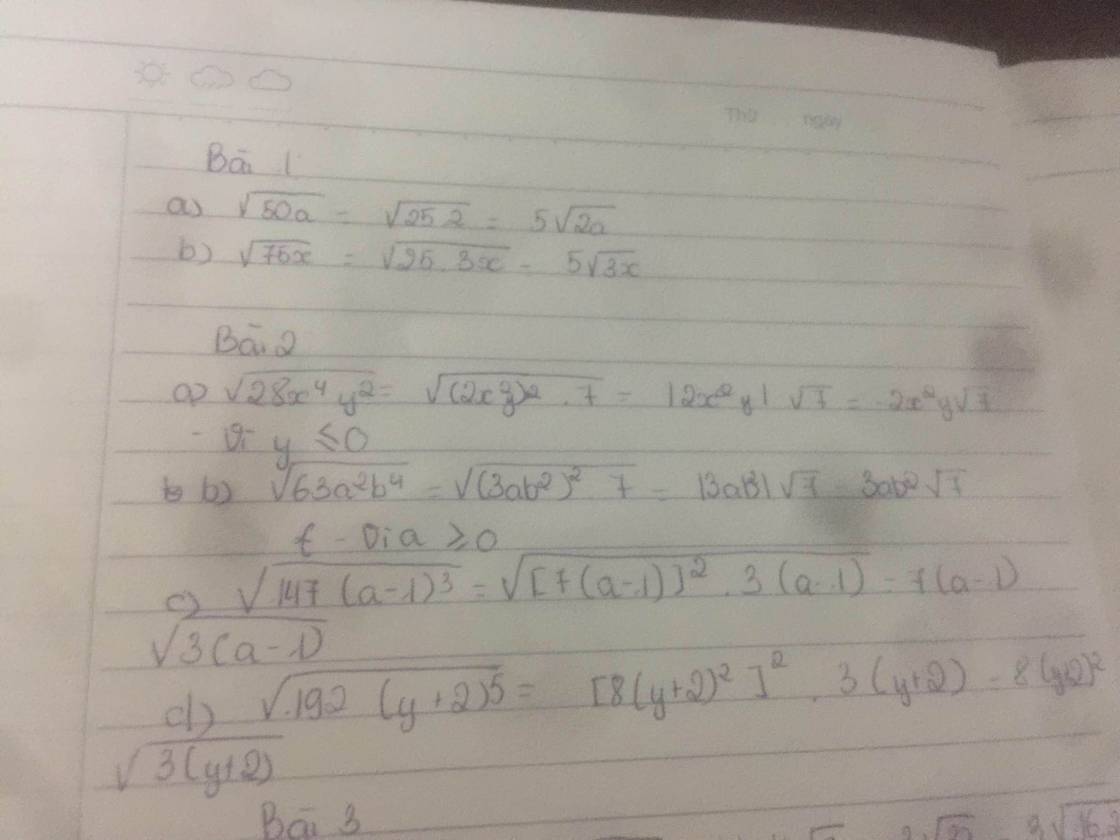chịu.-.

HT~~~

a/ \(\sqrt{50a}=5\sqrt{2a}\)

b/ \(\sqrt{75x}=5\sqrt{3x}\)

a)\(5\sqrt{2a}\)

b)\(5\sqrt{3x}\)

\(\frac{15}{3}-\frac{17}{4}+\frac{2}{8}+\frac{3}{5}-\frac{7}{10}\)

\(\Leftrightarrow\frac{600}{120}-\frac{510}{120}+\frac{30}{120}+\frac{72}{120}-\frac{84}{120}\)

\(\Leftrightarrow\frac{600-510+30+72-84}{120}\)

\(\Leftrightarrow\frac{108}{120}\)

\(\Leftrightarrow\frac{108:12}{120:12}=\frac{9}{10}\)

Xin lỗi nhé

Em mới học lớp 5 nên không biết đâu

47 + 47 = 94 Đúng 

47 - 47 =0 sai nhé tính tổng mà

Số hạng thứu 2 là 0

Vì số hạng thứ 1 bằng tổng

=>47-47=0

HT

Diện tích 2 lần tam giác là:

\(90\cdot2=180\left(cm^2\right)\)

Chiều cao của hình tam giác là:

\(180:15=12\left(cm\right)\)

Đáp số: \(12cm\)

Khái niệm: Muốn tính chiều cao của hình tam giác khi biết diện tích và đáy tương ứng thì ta lấy 2 lần diện tích hình tam giác chia cho đáy tương ứng.

Tích của đáy và chiều cao là  : 

    90 x 2 = 180 ( cm )

Chiều cao của hình tam giác là : 

  180 : 15 = 12 ( cm )

         Đ/s : 12 cm 

Như vậy, với bài toán cho biết hai dữ liệu là chiều cao và chiều dài cạnh đáy thì chúng ta áp dụng công thức S = (a x h) / 2. Trong đó S là diện tích, a là chiều dài đáy tam giác đều, h là chiều cao (đoạn thẳng từ đỉnh hạ xuống cạnh đáy).

diện tích tam giác là : \(\frac{axh}{2}\)suy ngược lại công thức tính độ dài đáy hình tam giác là a = \(\frac{sx2}{h}\)

diện tích hình thang là : \(\frac{\left(a+b\right)xh}{2}\)suy ngược lại công thức chiều cao và tổng độ dài hai đáy hình thang là

chiều cao : h = S x 2 : ( a+b )

độ dài hai đáy hình thang : a + b = S x 2 : h

/HT\

tl

10

ht

TL:

nhân với 10 nhé

HT

4,234 ; 4,24 ; 7,05; 7,1 ; 8,79

HT

156677