(x ^ 4 - x ^ 2 + 1)/(x ^ 2 * (1 - x ^ 2)) + 5/(2x * sqrt(1 - x ^ 2)) + 2 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Với \(x\ge0;x\ne1\):
\(P=\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right).\dfrac{\left(1-x\right)^2}{2}\)
\(=\left[\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}-\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}\right].\dfrac{\left(x-1\right)^2}{2}\)
\(=\dfrac{x-\sqrt{x}-2-\left(x+\sqrt{x}-2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}.\dfrac{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)^2}{2}\)
\(=\dfrac{-2\sqrt{x}\left(\sqrt{x}-1\right)}{2}=\sqrt{x}\left(1-\sqrt{x}\right)=\sqrt{x}-x\)
b, Thay \(x=7-4\sqrt{3}\) vào P, ta được:
\(P=\sqrt{7-4\sqrt{3}}-\left(7-4\sqrt{3}\right)\)
\(=\sqrt{\left(\sqrt{3}\right)^2-2.\sqrt{3}.2+2^2}+4\sqrt{3}-7\)
\(=\sqrt{\left(\sqrt{3}-2\right)^2}+4\sqrt{3}-7\)
\(=\left|\sqrt{3}-2\right|+4\sqrt{3}-7\)
\(=2-\sqrt{3}+4\sqrt{3}-7\) (vì \(\sqrt{3}< 2\))
\(=-5+3\sqrt{3}\)
$Toru$
a) \(P=\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right).\dfrac{\left(1-x\right)^2}{2}\left(x\ge0,x\ne1\right)\\ =\left[\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\right].\dfrac{\left(x-1\right)^2}{2}\\ =\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}.\dfrac{\left(x-1\right)^2}{2}\\ \)
\(=\dfrac{x-2\sqrt{x}+\sqrt{x}-2-\left(x+2\sqrt{x}-\sqrt{x}-2\right)}{\left(x-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\left(x-1\right)\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{2}\\ =\left[x-\sqrt{x}-2-\left(x+\sqrt{x}-2\right)\right].\dfrac{\sqrt{x}-1}{2}\\ \)
\(=-2\sqrt{x}.\dfrac{\sqrt{x}-1}{2}\\ =-\sqrt{x}\left(\sqrt{x}-1\right)=-x+\sqrt{x}\)
b) \(x=7-4\sqrt{3}\left(TMDK\right)\)
\(\sqrt{x}=\sqrt{\left(2-\sqrt{3}\right)^2}=\left|2-\sqrt{3}\right|=2-\sqrt{3}\)
Thay vào biểu thức P, ta được:
\(P=-\left(7-4\sqrt{3}\right)+2-\sqrt{3}=-5+3\sqrt{3}\)


Lời giải:
Áp dụng BĐT Bunhiacopxky:
$(\sqrt{2a+b}+\sqrt{2b+c}+\sqrt{2c+a})^2\leq [(2a+b)+(2b+c)+(2c+a)](1+1+1)=3(a+b+c).3=9(a+b+c)=81$
$\Rightarrow \sqrt{2a+b}+\sqrt{2b+c}+\sqrt{2c+a}\leq 9$
Vậy ta có đpcm
Dấu "=" xảy ra khi $a=b=c=3$

a: 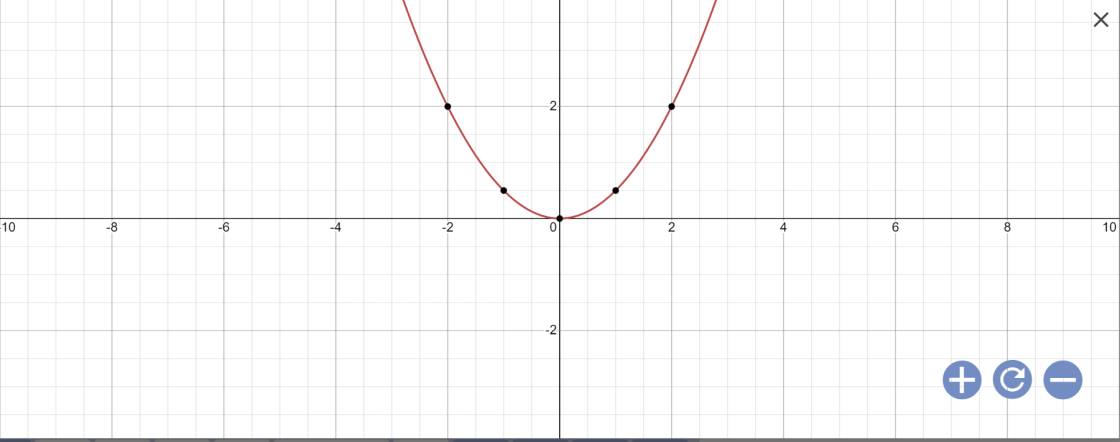
b: Thay x=0 và y=-2 vào (d1), ta được:
\(a\cdot0+b=-2\)
=>b=-2
=>(d1): y=ax-2
Thay x=1 và y=3 vào (d1), ta được:
\(a\cdot1-2=3\)
=>a-2=3
=>a=5
Vậy: (d1): y=5x-2
c: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=2x+m\)
=>\(x^2=4x+2m\)
=>\(x^2-4x-2m=0\)
\(\Delta=\left(-4\right)^2-4\cdot1\cdot\left(-2m\right)=8m+16\)
Để (P) cắt (d2) tại hai điểm phân biệt thì 8m+16>0
=>8m>-16
=>m>-2
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=4\\x_1x_2=\dfrac{c}{a}=-2m\end{matrix}\right.\)
\(x_1+x_2-2x_1x_2=2024\)
=>\(4-2\cdot\left(-2m\right)=2024\)
=>4m+4=2024
=>m+1=506
=>m=505(nhận)

\(x+\sqrt{x+2}=0\left(ĐK:x\ge-2\right)\)
\(\Leftrightarrow x+1+\left(\sqrt{x+2}-1\right)=0\\ \Leftrightarrow x+1+\dfrac{x+2-1}{\sqrt{x+2}+1}=0\\ \Leftrightarrow x+1+\dfrac{x+1}{\sqrt{x+2}+1}=0\\ \Leftrightarrow\left(x+1\right)\left(1+\dfrac{1}{\sqrt{x+2}+1}\right)=0\\ \Rightarrow\left[{}\begin{matrix}x+1=0\\1+\dfrac{1}{\sqrt{x+2}+1}=0\left(PTVN\right)\end{matrix}\right.\Leftrightarrow x=-1\left(TMDK\right)\)
Vậy pt có nghiệm duy nhất: x=-1
Mình giải thích thêm phần này nhé:
\(1+\dfrac{1}{\sqrt{x+2}+1}=0\left(PTVN\right)\)
Vì với mọi x thuộc ĐK:
\(\sqrt{x+2}\ge0\Rightarrow\sqrt{x+2}+1>0\\ \Rightarrow\dfrac{1}{\sqrt{x+2}+1}>0\\ \Rightarrow VT=1+\dfrac{1}{\sqrt{x+2}+1}>0=VP\)
Do VT > VP nên không thể xảy ra dấu =
Dẫn đến ptvn bạn nhé



Em nên viết bằng công thức toán học có biểu tượng Σ góc trái màn hình em nhé. Như vậy mọi người mới hiểu đúng đề được để có thể hỗ trợ tốt nhất cho em.

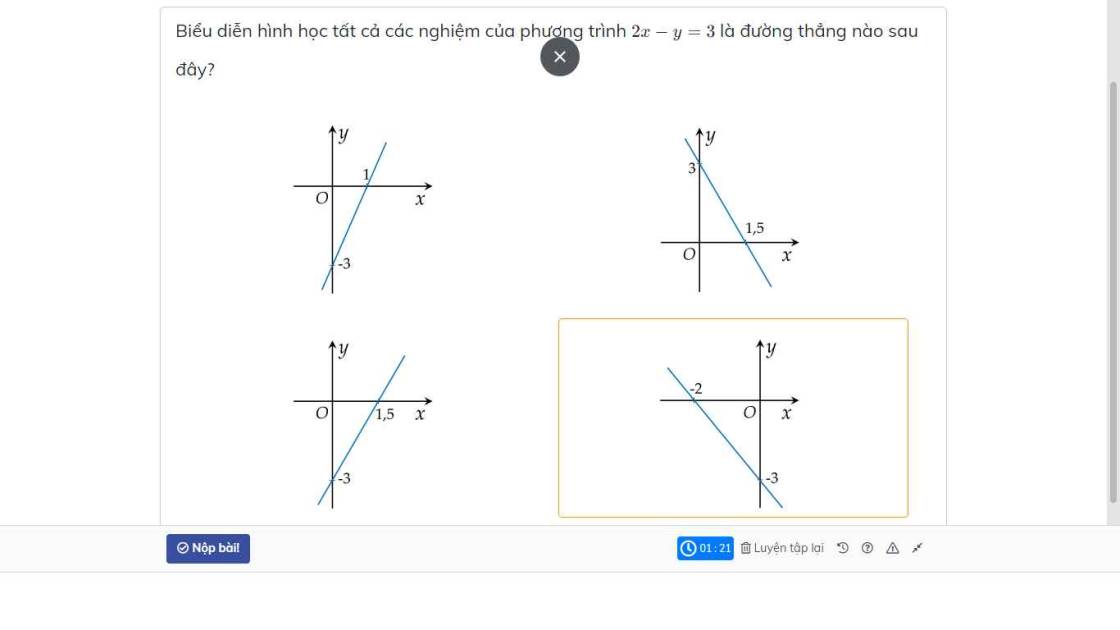
Ta có pt: $2x-y=3$ (1)
+, $y=0\Rightarrow 2x=3\Leftrightarrow x=1,5$
$\Rightarrow (1,5;0)$ là giao điểm của pt (1) với trục hoành
+, $x=0\Rightarrow -y=3\Leftrightarrow y=-3$
$\Rightarrow (0;-3)$ là giao điểm của pt (1) với trục tung
Kẻ đường thẳng đi qua hai điểm trên, ta được đường thẳng biểu diễn các nghiệm của pt $2x-y=3$
$\Rightarrow$ Chọn đáp án:


Ta có \(x+y+xy=3\Leftrightarrow-xy=x+y-3\). Khi đó \(P=\dfrac{3}{x+y}+x+y-3\)
Đặt \(x+y=t\left(t>0\right)\). Khi đó: \(P=\dfrac{3}{t}+t-3\)
Lại có \(xy\le\dfrac{\left(x+y\right)^2}{4}\) \(\Leftrightarrow3=x+y+xy\le\left(x+y\right)+\dfrac{\left(x+y\right)^2}{4}\) \(=t+\dfrac{t^2}{4}\)
\(\Leftrightarrow t^2+4t\ge12\) \(\Leftrightarrow t\ge2\)
Khi đó \(P=\dfrac{3}{t}+t-3=\dfrac{3}{t}+\dfrac{3}{4}t+\dfrac{t}{4}-3\)
\(\ge2\sqrt{\dfrac{3}{t}.\dfrac{3}{4}t}+\dfrac{2}{4}-3\) (chú ý rằng \(t\ge2\))
\(=2.\dfrac{3}{2}+\dfrac{1}{2}-3\)
\(=\dfrac{1}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}t=2\\\dfrac{3}{t}=\dfrac{3}{4}t\end{matrix}\right.\Leftrightarrow t=2\) \(\Leftrightarrow x+y=2\) \(\Rightarrow xy=1\)
\(\Rightarrow x=y=1\)
Vậy \(minP=\dfrac{1}{2}\) khi \(x=y=1\)
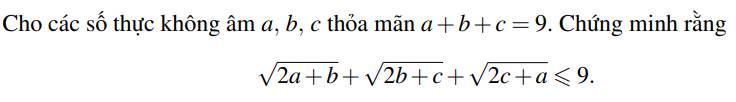



Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người đọc hiểu đề và hỗ trợ bạn nhanh hơn nhé.