Mua mảnh vườn hình chữ nhật có tổng độ dài hai cạnh liên tiếp là 135 m chiều dài hơn chiều rộng Tính diện tích của mảnh vườn đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 3:
a:
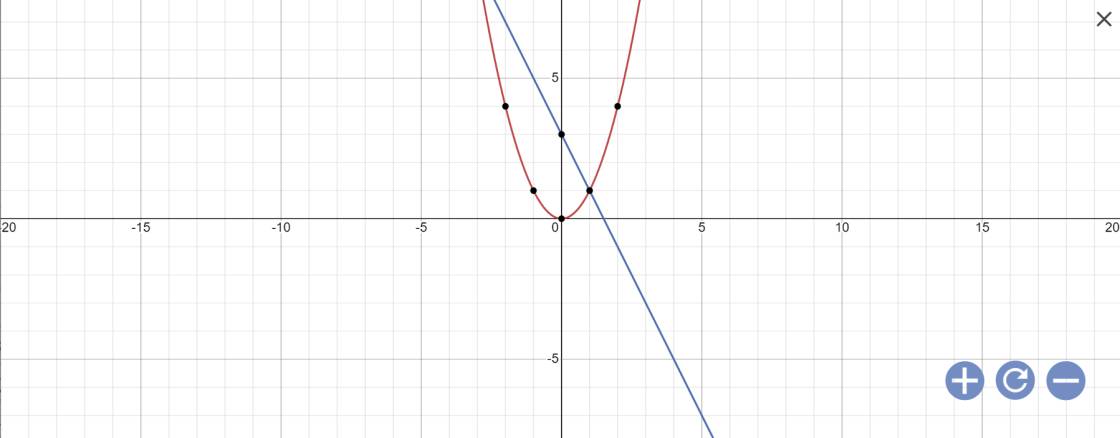
b: Phương trình hoành độ giao điểm là:
\(x^2=-2x+3\)
=>\(x^2+2x-3=0\)
=>(x+3)(x-1)=0
=>\(\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)
Khi x=-3 thì \(y=\left(-3\right)^2=9\)
Khi x=1 thì \(y=1^2=1\)
Vậy: (P) cắt (d) tại A(-3;9); B(1;1)
Câu 4:
a:
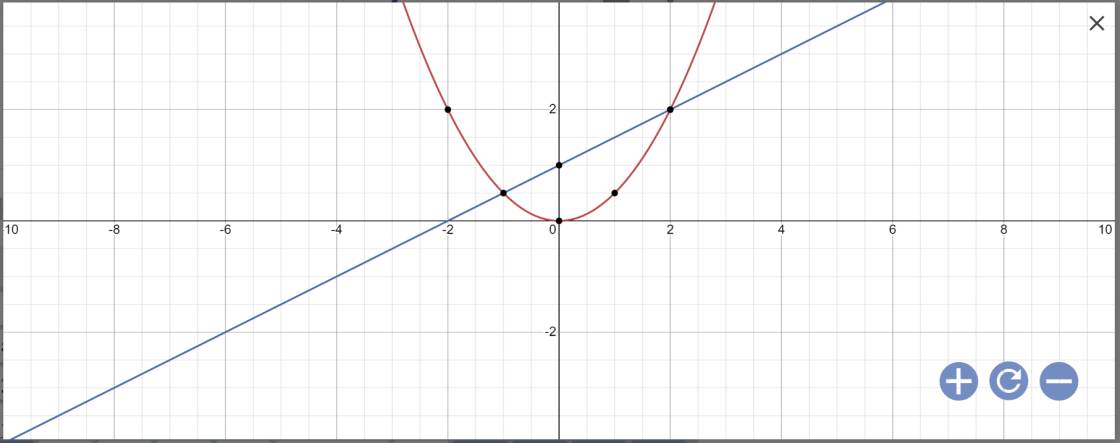
b: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=\dfrac{1}{2}x+1\)
=>\(x^2=x+2\)
=>\(x^2-x-2=0\)
=>(x-2)(x+1)=0
=>\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Khi x=2 thì \(y=\dfrac{1}{2}\cdot2^2=2\)
Khi x=-1 thì \(y=\dfrac{1}{2}\cdot\left(-1\right)+1=1-\dfrac{1}{2}=\dfrac{1}{2}\)
vậy: \(A\left(2;2\right);B\left(-1;\dfrac{1}{2}\right)\)
c: Thay x=1 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot1^2=\dfrac{1}{2}\)
vậy: C(1;0,5)
A(2;2); B(-1;0,5); C(1;0,5)
\(AB=\sqrt{\left(-1-2\right)^2+\left(0,5-2\right)^2}=\dfrac{3\sqrt{5}}{2}\)
\(AC=\sqrt{\left(1-2\right)^2+\left(0,5-2\right)^2}=\dfrac{\sqrt{13}}{2}\)
\(BC=\sqrt{\left(1+1\right)^2+\left(0,5-0,5\right)^2}=2\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{\dfrac{45}{4}+\dfrac{13}{4}-4}{2\cdot\dfrac{3\sqrt{5}}{2}\cdot\dfrac{\sqrt{13}}{2}}=\dfrac{7}{\sqrt{65}}\)
=>\(sinBAC=\sqrt{1-\left(\dfrac{7}{\sqrt{65}}\right)^2}=\dfrac{4}{\sqrt{65}}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(=\dfrac{1}{2}\cdot\dfrac{4}{\sqrt{65}}\cdot\dfrac{3\sqrt{5}}{2}\cdot\dfrac{\sqrt{13}}{2}=\dfrac{3}{2}\)

Giải
Số cần tìm là:
(80% : 2 - 0,075) x 6 = 1,95
Số cần tìm là 1,95

Câu 2: \(\dfrac{x}{6}+\dfrac{y}{8}=1\)
=>\(\dfrac{4x+3y}{24}=1\)
=>4x+3y=24
=>4x+3y-24=0
Khoảng cách từ O đến đường thẳng 4x+3y-24=0 là:
\(d\left(O;4x+3y-24=0\right)=\dfrac{\left|0\cdot4+0\cdot3-24\right|}{\sqrt{3^2+4^2}}=\dfrac{24}{5}=4,8\)

M(1/2)=0
=>\(a\cdot\left(\dfrac{1}{2}\right)^2+5\cdot\dfrac{1}{2}-3=0\)
=>\(a\cdot\dfrac{1}{4}=\dfrac{1}{2}\)
=>\(a=\dfrac{1}{2}:\dfrac{1}{4}=2\)
Vì M(\(x\)) = a\(x^2\) + 5\(x\) - 3
M(\(\dfrac{1}{2}\)) = 0
a.(\(\dfrac{1}{2}\))2 + 5.(\(\dfrac{1}{2}\)) - 3 = 0
\(\dfrac{1}{4}\)a + \(\dfrac{5}{2}\) - 3 = 0
\(\dfrac{1}{4}\)a - \(\dfrac{1}{2}\) = 0
\(\dfrac{1}{4}\)a = \(\dfrac{1}{2}\)
a = \(\dfrac{1}{2}\) : \(\dfrac{1}{4}\)
a = 2
Vậy để \(x\) = \(\dfrac{1}{2}\) là nghiệm của đa thức thì a = 2

a: Thời gian người đó đi hết quãng đường là:
7h15p-6h30p=45p=0,75(h)
Độ dài quãng đường AB là 0,75x40=30(km)
b: Vận tốc của ô tô là \(40\times\dfrac{2}{3}=\dfrac{80}{3}\left(\dfrac{km}{h}\right)\)
Thời gian ô tô đi hết quãng đường là:
\(30:\dfrac{80}{3}=30\times\dfrac{3}{80}=\dfrac{9}{8}\left(giờ\right)\)

1: \(\dfrac{26}{7}\left[\left(-\dfrac{7}{5}\right)-\dfrac{3}{2}:\dfrac{-5}{-4}+\left(\dfrac{3}{2}\right)^2\right]\)
\(=\dfrac{26}{7}\left(-\dfrac{7}{5}+\dfrac{3}{2}\cdot\dfrac{4}{5}+\dfrac{9}{4}\right)\)
\(=\dfrac{26}{7}\left(-\dfrac{7}{5}+\dfrac{3}{10}+\dfrac{9}{4}\right)\)
\(=\dfrac{26}{7}\cdot\dfrac{-28+6+45}{20}=\dfrac{26}{20}\cdot\dfrac{23}{7}=\dfrac{23}{7}\cdot\dfrac{13}{10}=\dfrac{299}{70}\)
2: \(\dfrac{2}{7}+\dfrac{5}{7}\left(\dfrac{3}{5}-0,25\right)\cdot\left(-2\right)^2+35\%\)
\(=\dfrac{2}{7}+\dfrac{5}{7}\left(\dfrac{3}{5}-\dfrac{1}{4}\right)\cdot4+\dfrac{7}{20}\)
\(=\dfrac{89}{140}+\dfrac{20}{7}\cdot\dfrac{7}{20}\)
\(=\dfrac{89}{140}+1=\dfrac{229}{140}\)

a) Chỉ có 1 khả năng xuất hiện mặt có số chấm bằng 4 trong 6 khả năng nên P(A) = 1616.
b) Chỉ có 1 khả năng xuất hiện mặt có số chấm bằng 5 là số chia hết cho 5 trong 6 khả năng nên P(B) = 1616.
c) Không có mặt nào có số chấm là số tròn chục nên biến cố C là biến cố không thể.
Do đó P(C) = 0.
a:
\(\Omega=\left\{1;2;3;4;5;6\right\}\)
=>\(n\left(\Omega\right)=6\)
Gọi A là biến cố "Gieo được mặt có số chấm là 4"
=>A={4}
=>n(A)=1
=>\(P\left(A\right)=\dfrac{1}{6}\)
b: Gọi B là biến cố "Gieo được mặt có số chấm là số lẻ"
=>B={1;3;5}
=>n(B)=3
=>\(P\left(B\right)=\dfrac{3}{6}=\dfrac{1}{2}\)
c: Gọi C là biến cố "Gieo được mặt có số chấm lớn hơn 1"
=>C={2;3;4;5;6}
=>n(C)=5
\(P\left(C\right)=\dfrac{5}{6}\)


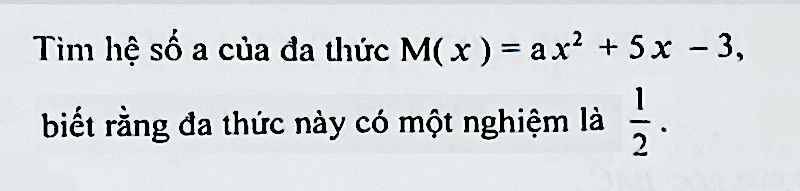
chiều dài hơn chiều rộng bao nhiêu m vậy em?
Hơn1 ạ