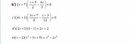\(\frac{x^2-2x+2}{x-1}+\frac{x^2-8x+20}{x-4}=\frac{x^2-4x+6}{x-2}+\frac{x^2-6x+12}{x-3}\)\(ĐKXĐ:x\ne1;2;3;4\)

\(\Leftrightarrow\frac{\left(x-1\right)^2+1}{x-1}+\frac{\left(x-4\right)^2+4}{x-4}=\frac{\left(x-2\right)^2+2}{x-2}+\frac{\left(x-3\right)^2+3}{x-3}\)

\(\Leftrightarrow\left(\frac{\left(x-1\right)^2}{x-1}+\frac{1}{x-1}\right)+\left(\frac{\left(x-4\right)^2}{x-4}+\frac{4}{x-4}\right)=\left(\frac{\left(x-2\right)^2}{x-2}+\frac{2}{x-2}\right)+\left(\frac{\left(x-3\right)^2}{x-3}+\frac{3}{x-3}\right)\)

\(\Leftrightarrow x-1+\frac{1}{x-1}+x-4+\frac{1}{x-4}=x-2+\frac{1}{x-2}+x-3+\frac{1}{x-3}\)

\(\Leftrightarrow\frac{1}{x-1}+\frac{4}{x-4}=\frac{2}{x-2}+\frac{3}{x-3}\)

\(\Leftrightarrow\frac{x-4+4x-4}{\left(x-1\right)\left(x-4\right)}=\frac{2x-6+3x-6}{\left(x-2\right)\left(x-3\right)}\)

\(\Leftrightarrow\frac{5x-8}{x^2-5x+4}=\frac{5x-12}{x^2-5x+6}\)

\(\Leftrightarrow\left(5x-8\right)\left(x^2-5x+6\right)=\left(5x-12\right)\left(x^2-5x+4\right)\)

Tự giải ra rồi tìm x nhé

dấu suy ra số 4 là 1/(x+1) + 1/(x+4) mà.

Trả lời:

b, \(\left(x+7\right)\left(\frac{x+5}{2}-\frac{4x}{3}\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+7=0\\\frac{x+5}{2}-\frac{4x}{3}=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-7\\x=3\end{cases}}}\)

Vậy S = { -7; 3 }

Tự kết luận nghiệm nhé 

b, \(\left(x+7\right)\left(\frac{x+5}{2}-\frac{4x}{3}\right)=0\)

TH1 : \(x+7=0\Leftrightarrow x=-7\)

TH2 : \(\frac{3x+15}{6}-\frac{8x}{6}=0\Leftrightarrow\frac{-5x+15}{6}=0\Leftrightarrow x=3\)

c, \(\left(4x+3\right)\left(\frac{3x+7}{4}-\frac{x-3}{12}\right)=0\)

\(\Leftrightarrow\left(4x+3\right)\left(\frac{9x-21}{12}-\frac{x-3}{12}\right)=0\)

TH1 : \(4x+3=0\Leftrightarrow x=-\frac{3}{4}\)

TH2 : \(\frac{9x-21-x+3}{12}=0\Leftrightarrow8x-18=0\Leftrightarrow x=\frac{9}{4}\)

d, \(\left(2x+1\right)\left(1-x\right)+2x=2\Leftrightarrow\left(2x+1\right)\left(1-x\right)+2\left(x-1\right)=0\)

\(\Leftrightarrow\left(2x+1\right)\left(1-x\right)-2\left(1-x\right)=0\Leftrightarrow\left(1-x\right)\left(2x-1\right)=0\Leftrightarrow x=1;x=\frac{1}{2}\)

e, \(\left(x-2\right)\left(x^2-3x+5\right)=x^3-2x^2\)

\(\Leftrightarrow\left(x-2\right)\left(x^2-3x+5\right)-x^2\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(-3x+5\right)=0\Leftrightarrow x=2;x=-\frac{5}{3}\)

Xét \(\Delta ABC\)vuông tại A theo định lí Pitago ta có : \(AB^2+AC^2=BC^2\Rightarrow6^2+8^2=BC^2\)

\(\Rightarrow BC=\sqrt{6^2+8^2}=10\left(cm\right)\)

Xét \(\Delta DEF\)vuông tại D theo định lí Pitago ta có :\(DE^2+DF^2=EF^2\)

=> \(DF^2=EF^2-DE^2=15^2-9^2=144\)

=> \(DF=\sqrt{144}=12\left(cm\right)\)

Để hai tam giác trên đồng dạng với nhau , trước hết tính tỉ lệ tương ứng với 3 cạnh

Xét tam giác ABC và tam giác DEF ta có :

\(\frac{AB}{DE}=\frac{6}{9}=\frac{2}{3}\)

\(\frac{BC}{EF}=\frac{10}{15}=\frac{2}{3}\)

\(\frac{AC}{DF}=\frac{8}{12}=\frac{2}{3}\)

=> \(\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}\left(=\frac{2}{3}\right)\)

=> Tam giác ABC đồng dạng tam giác DEF

Nếu bạn muốn làm tam giác DEF đồng dạng với tam giác ABC cũng được

ko b oi

gọi x (giờ)  là thời gian tính từ lúc khởi hành đến lúc khoảng cách từ ngườ 1 đến B gấp đôi người 2 đến B

ta có 

\(60-12x=2\left(60-15x\right)\)

\(\Leftrightarrow18x=60\Leftrightarrow x=\frac{10}{3}\text{ giờ }=3\text{ giờ 20 phút}\)

ĐKXĐ : \(x\ne\pm\frac{2}{3}\)

Ta có : \(\frac{3x+5}{3x+2}+\frac{3x+15}{9x^2-4}=\frac{2}{3x-2}\)

\(\Leftrightarrow\frac{\left(3x+5\right)\left(3x-2\right)}{\left(3x-2\right)\left(3x+2\right)}+\frac{3x+15}{\left(3x-2\right)\left(3x+2\right)}=\frac{2\left(3x+2\right)}{\left(3x-2\right)\left(3x+2\right)}\)

\(\Leftrightarrow\frac{9x^2+9x-10}{\left(3x-2\right)\left(3x+2\right)}+\frac{3x+15}{\left(3x-2\right)\left(3x+2\right)}=\frac{6x+4}{\left(3x-2\right)\left(3x+2\right)}\)

\(\Leftrightarrow\frac{9x^2+12x+5}{\left(3x-2\right)\left(3x+2\right)}=\frac{6x+4}{\left(3x-2\right)\left(3x+2\right)}\)

\(\Rightarrow9x^2+12x+5=6x+4\)

\(\Leftrightarrow9x^2+6x+1=0\)

\(\Leftrightarrow\left(3x+1\right)^2=0\)

\(\Leftrightarrow3x+1=0\)

\(\Leftrightarrow x=-\frac{1}{3}\)(Thỏa mãn)

Vậy tập nghiệm của PT là \(S=\left\{-\frac{1}{3}\right\}\)

\(\frac{3x+5}{3x+2}+\frac{3x+15}{9x^2-4}=\frac{2}{3x-2}\)

\(ĐKXĐ:x\ne\pm\frac{2}{3}\)

\(\Leftrightarrow\frac{\left(3x+5\right)\left(3x-2\right)}{\left(3x-2\right)\left(3x+2\right)}+\frac{3x+15}{\left(3x-2\right)\left(3x+2\right)}=\frac{2\left(3x+2\right)}{\left(3x-2\right)\left(3x+2\right)}\)

\(\Rightarrow9x^2+9x-10+3x+15=6x+4\)

\(\Leftrightarrow9x^2+12x+5-6x-4=0\)

\(\Leftrightarrow9x^2+6x+1=0\)

\(\Leftrightarrow\left(3x+1\right)^2=0\)

\(\Leftrightarrow3x+1=0\)

\(\Leftrightarrow x=-\frac{1}{3}\left(tm\right)\)

Vậy phương trình có nghiệm duy nhất x = -1/3