hai vòi nước cùng chảy vào bể. Nếu vòi thứ nhất chảy riêng một mình thì sau 30 giờ sẽ đầy bể. Nếu vòi thứ hai chảy riêng một mình thì cần 12 giờ để chảy đầy bể. Hỏi cả hai vòi cùng chảy thì sau bao lâu bể sẽ đầy?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔKNP vuông tại N và ΔHPN vuông tại H có
NP chung
\(\widehat{KNP}=\widehat{HPN}\)
Do đó: ΔKNP=ΔHPN
b: Ta có;ΔKNP=ΔHPN
=>\(\widehat{KPN}=\widehat{HNP}\)
=>\(\widehat{ENP}=\widehat{EPN}\)
=>ΔENP cân tại E
c: Xét ΔMNE và ΔMPE có
MN=MP
EN=EP
ME chung
Do đó: ΔMNE=ΔMPE
=>\(\widehat{NME}=\widehat{PME}\)
=>ME là phân giác của góc NMP

Để giải bài toán này, chúng ta cần tìm tất cả các số có ba chữ số khác nhau mà mỗi chữ số đều là số chẵn. Các số chẵn từ 0 đến 9 là: 0, 2, 4, 6, và 8.
Chữ số hàng trăm: Có 4 lựa chọn (2, 4, 6, 8) vì chữ số hàng trăm không thể là 0.
Chữ số hàng chục: Sau khi chọn chữ số hàng trăm, còn lại 4 lựa chọn cho chữ số hàng chục (không thể giống chữ số hàng trăm và không thể là 0 nếu chữ số hàng trăm đã chọn là 0).
Chữ số hàng đơn vị: Còn lại 3 lựa chọn cho chữ số hàng đơn vị (không thể giống hai chữ số đã chọn).
Vậy, số các số có ba chữ số khác nhau mà mỗi chữ số đều là số chẵn là:
4 x 4 x 3 = 48 số.
Như vậy, có 48 số thỏa mãn điều kiện của bài toán.

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
=>\(\dfrac{AC}{HA}=\dfrac{BC}{BA}=\dfrac{AB}{HB}\)
=>\(AB\cdot HA=AC\cdot HB\)
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{15^2+20^2}=25\left(cm\right)\)
\(\dfrac{BC}{BA}=\dfrac{AC}{HA}\)
=>\(HA=\dfrac{AB\cdot AC}{BC}=\dfrac{15\cdot20}{25}=\dfrac{300}{25}=12\left(cm\right)\)
=>\(HB=\sqrt{15^2-12^2}=9\left(cm\right)\)
c:
Xét ΔBAH có BI là phân giác
nên \(\dfrac{IA}{IH}=\dfrac{BA}{BH}\left(1\right)\)
Xét ΔBAC có BD là phân giác
nên \(\dfrac{DC}{DA}=\dfrac{BC}{BA}\left(2\right)\)
Ta có: ΔBHA~ΔBAC
=>\(\dfrac{BA}{BC}=\dfrac{BH}{BA}\)
=>\(\dfrac{BC}{BA}=\dfrac{BA}{BH}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{IA}{IH}=\dfrac{DC}{DA}\)
=>\(IA\cdot DA=DC\cdot IH\)

a: \(A=\left(2x+y\right)\left(2x-y\right)=\left(2x\right)^2-y^2=4x^2-y^2\)
Khi x=-2 và y=1/3 thì \(A=4\cdot\left(-2\right)^2-\left(\dfrac{1}{3}\right)^2=16-\dfrac{1}{9}=\dfrac{143}{9}\)
b: x(3x-2)-3x2=3/4
=>\(3x^2-2x-3x^2=\dfrac{3}{4}\)
=>\(-2x=\dfrac{3}{4}\)
=>\(x=-\dfrac{3}{4}:2=-\dfrac{3}{8}\)


a: Xét ΔBAH và ΔBIH có
BA=BI
AH=IH
BH chung
Do đó: ΔBAH=ΔBIH
b: Ta có: ΔBAH=ΔBIH
=>\(\widehat{ABE}=\widehat{IBE}\)
Xét ΔBAE và ΔBIE có
BA=BI
\(\widehat{ABE}=\widehat{IBE}\)
BE chung
Do đó: ΔBAE=ΔBIE
=>EA=EI
c: Ta có: ΔBAE=ΔBIE
=>\(\widehat{BAE}=\widehat{BIE}\)
=>\(\widehat{BIE}=90^0\)
=>EI\(\perp\)BC tại I
ta có: EA=EI
mà EA<EM(ΔEAM vuông tại A)
nên EM>EI

Tỉ số giữa số bạn nữ và số học sinh cả lớp là:
\(\dfrac{2}{3+2}=\dfrac{2}{5}\)
Số bạn nữ là \(35\times\dfrac{2}{5}=14\left(bạn\right)\)
Giải
Số bạn nữ bằng: 2 : (3 + 2) = \(\dfrac{2}{5}\) (số học sinh cả lớp)
Số học sinh nữ là: 35 x \(\dfrac{2}{5}\) = 14 (bạn)
Số học sinh nam là: 35 - 14 = 21 (bạn)
Số học sinh nữ nam nhiều hơn số học sinh nữ là:
21 - 14 = 8 (bạn)
Đáp số:...

a: Xét ΔABC có
AM,BN,CP là các đường trung tuyến
AM,BN,CP cắt nhau tại G
Do đó: G là trọng tâm của ΔABC
=>\(BG=\dfrac{2}{3}BN;CG=\dfrac{2}{3}CP;AG=\dfrac{2}{3}AM;AG=2GM\)
=>BG=2GN; CG=2GP
Xét tứ giác BGCQ có
M là trung điểm chung của BC và GQ
=>BGCQ là hình bình hành
=>BQ=CG=2/3CP; BG=CQ=2/3BN
Ta có: AG=2GM
mà GQ=2GM
nên GQ=GA
=>\(GQ=\dfrac{2}{3}AM\)
=>Δcác cạnh của tam giác BQG=2/3 độ dài của các đưòng trung tuyến của tam giác ABC
b: Sửa đề: BM<1/2(BG+BQ)
Xét ΔGBC có GB+GC>BC
=>GB+BQ>2BM
=>\(BM< \dfrac{1}{2}\left(BG+BQ\right)\)
c: Ta có: AG=GQ
=>G là trung điểm của AQ
Các đường trung tuyến của ΔBCQ là GK,QI,BM
Xét ΔQAB có
K,G lần lượt là trung điểm của QB,QA
=>KG là đường trung bình của ΔQAB
=>KG=1/2AB
Ta có: I là trung điểm của BG
=>BI=IG=BG/2
mà GN=BG/2
nên BI=IG=GN
=>G là trung điểm của IN
Xét tứ giác ANQI có
G là trung điểm chung của AQ và NI
=>ANQI là hình bình hành
=>\(QI=AN=\dfrac{AC}{2}\)
Vì M là trung điểm của BC
nên \(BM=\dfrac{1}{2}BC\)
=>ĐPCM

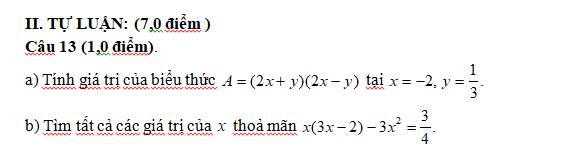
Trong 1 giờ, vòi thứ nhất chảy được \(\dfrac{1}{30}\left(bể\right)\)
Trong 1 giờ, vòi thứ hai chảy được \(\dfrac{1}{12}\left(bể\right)\)
Trong 1 giờ, hai vòi chảy được \(\dfrac{1}{30}+\dfrac{1}{12}=\dfrac{2}{60}+\dfrac{5}{60}=\dfrac{7}{60}\left(bể\right)\)
=>Hai vòi cần \(1:\dfrac{7}{60}=\dfrac{60}{7}\) giờ để chảy đầy bể