Năm 1003 thuộc thế kỉ 11

năm 1003 thuộc thế kỉ 10

Tích mới hơn tích cũ là:

2604 - 1932 = 672

Số thứ 2 là:

672 : 8 = 84

Số thứ 1 là:

1932 : 84 = 23

Tích mới là

2604-1932=672

số thứ hai là

672:8=84

Giải toán bằng phương pháp giải ngược của tiểu học em nhé 

Giả sử lần thứ hai bà chỉ bán \(\dfrac{2}{3}\) số cam còn lại thì số cam còn lại sau lần bán thứ hai là:

                 2 + 2  = 4 ( quả)

4 quả ứng với phân số là:

1 - \(\dfrac{2}{3}\)=\(\dfrac{1}{3}\) (số cam còn lại sau lần bán thứ nhất)

Số cam còn lại sau lần bán thứ nhất là:

4 : \(\dfrac{1}{3}\) = 12 (quả)

Giả sử lần thứ nhất bà chỉ bán \(\dfrac{2}{3}\) số cam thì số cam còn lại sau lần bán thứ nhất là:

12 + 1 = 13 (quả)

13 quả ứng với phân số là: 

 1 - \(\dfrac{2}{3}\) = \(\dfrac{1}{3}\) (số cam)

Lúc đầu bà có tất cả số cam là: 

13 : \(\dfrac{1}{3}\) = 39 ( quả)

Đáp số: 39 quả

Thử lại ta có:

Lần thứ nhất bà bán: 39 \(\times\) \(\dfrac{2}{3}\) + 1 = 27 (quả)

Số cam còn lại sau lần bán thứ nhất là: 39 - 27 =12 (quả)

Số cam bà bán lần thứ hai là: 12 \(\times\) \(\dfrac{2}{3}\) + 2  =10 (quả)

Số cam còn lại sau hai lần bán là: 12 - 10 = 2 (quả) (ok em ha)

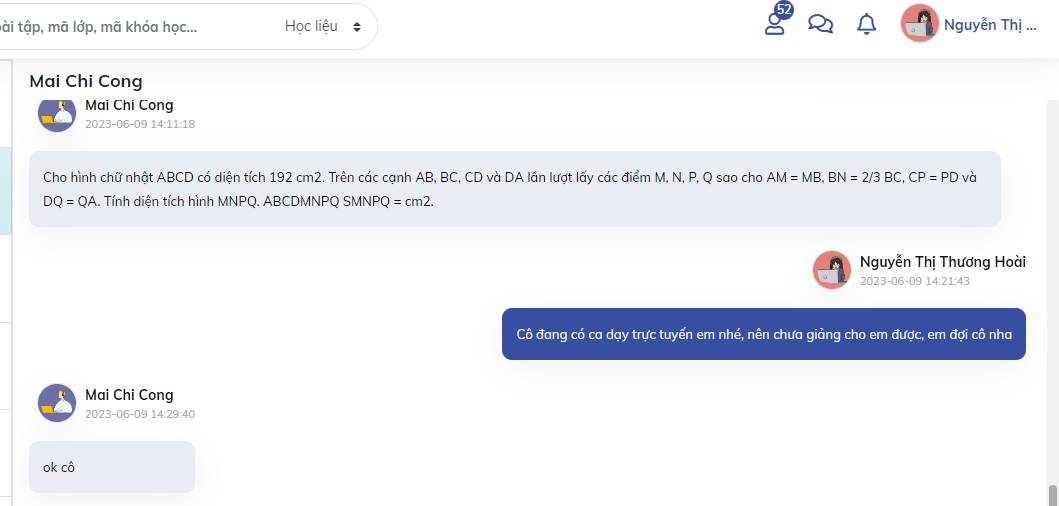
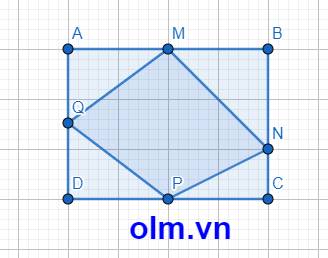
S_MNB = \(\dfrac{1}{2}\)S_ABN (Vì hai tam giác có chung chiều cao hạ từ đỉnh N xuông đáy AB và AM = \(\dfrac{1}{2}\)AB)

S_ABN = \(\dfrac{2}{3}\)S_ABC (Vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đày BC và BN = \(\dfrac{2}{3}\)BC)

S_MNB = \(\dfrac{1}{2}\) \(\times\) \(\dfrac{2}{3}\)S_ABC = \(\dfrac{1}{3}\)S_ABC = \(\dfrac{1}{6}\) S_ABCD = 192 \(\times\) \(\dfrac{1}{6}\) = 32 (cm²)

S_AMQ = S_DQP = \(\dfrac{1}{2}\)S_CDQ (Vì hai tam giác có chung chiều cao hạ từ đỉnh Q xuống đáy DC và DP = \(\dfrac{1}{2}\)DC)

S_CDQ = \(\dfrac{1}{2}\)S_ACD (Vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AD và DQ = \(\dfrac{1}{2}\) AD)

S_AMQ = S_PDQ = \(\dfrac{1}{2}\times\dfrac{1}{2}\)S_ACD  = \(\dfrac{1}{4}\)S_ACD  = \(\dfrac{1}{8}\)S_ABCD = 192\(\times\)\(\dfrac{1}{8}\)=24(cm²)

CN = BC - BN = BC - \(\dfrac{2}{3}\) BC =  \(\dfrac{1}{3}\)BC

S_CNP = \(\dfrac{1}{3}\)S_BCP (vì hai tam giác có chung chiều cao hạ từ đỉnh p xuống đáy BC)

S_BCP = \(\dfrac{1}{2}\)S_BCD(vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy CD và CP = \(\dfrac{1}{2}\) DC)

S_CNP  = \(\dfrac{1}{3}\times\dfrac{1}{2}\)S_BCD = \(\dfrac{1}{6}\)S_BCD = \(\dfrac{1}{12}\)S_ABCD =192\(\times\)\(\dfrac{1}{12}\)=16 (cm²)

S_MNPQ=S_ABCD - (S_MNB + S_AMQ + S_DPQ + S_CNP)

S_MNPQ = 192 - (32+24+24+16) = 96 (cm²)

Đáp số 96 cm²

X = {5; 7; 9; 11; 13;...;89}

Xét dãy số: 5; 7; 9; 11; 13;...;89

Dãy số trên là dãy số cách đều với khoảng cách là: 7 - 5 = 2

Phần tử đứng thứ 12 của tập hợp X là số thứ 12 của dãy số trên.

Áp dụng công thức tìm số thứ n của dãy số cách đều:

St_n = số đầu + Khoảng cách \(\times\)( n -1)

Số thứ 12 của dãy số trên là: 5 + 2 \(\times\) (12 - 1) = 27

Vậy phần tử đứng thứ 12 của tập hợp X từ trái qua phải khi các phần tử của tập hợp X được sắp theo thứ tự từ bé đến lớn là: 27

Ta có DE = EF = FB, và đoạn BD chia đoạn thẳng DE, EF, FB thành 3 đoạn, mỗi đoạn bằng:

12 : 3 = 4 ( cm )

Kẻ hình thành 2 tam giác là tam giác AEB và tam giác CDF bằng nhau:

Diện tích của tam giác AEB = tam giác CDF là:

4 x 12 : 2 = 24 ( cm² )

Diện tích của hình vuông ABCD là:

12 x 12 = 144 ( cm² )

Diện tích của AECF là: 

144 - ( 24 x 2 ) = 96 ( cm² )

Vậy diện tích của AECF là 96 cm²

Đổi: 75% = \(\dfrac{3}{4}\)

Tổng số phần bằng nhau là:

3 + 4 = 7 ( phần )

Số học sinh nam là:

28 : 7 : 3 = 12 ( học sinh )

Vậy số học sinh nam là: 12 học sinh

đổi :  `75% = 3/4 `

Tổng số phần bằng nhau là : ` 3 + 4 = 7 ` ( phần ) 

Số học sinh nam của lớp 5A là : `28 : 7 xx 3 = 12` ( h/s ) 

        Đáp số : 12 học sinh nam

Vì ta bỏ chữ số 1 ở tận cùng của một số đi thì được số mới nên số cũ gấp số mới 10 lần và 1 đơn vị

Ta có sơ đồ:

Theo sơ đồ ta có:

Số mới là: (406 -1): (10 -1) = 45

Số cần tìm là: 45 + 406 = 451

Đáp số: 451

Thử lại kết quả bài toán ta có: Số cần tìm là 451

Bỏ đi chữ số 1 của số 451 ta được số mới là 45

Số ban đầu hơn số mới là: 451 - 45 = 406 (ok)

Số mới là 

(406-1):(10-1)=45

số cần tìm là 

45+406=451

Đáp số :451

\(\dfrac{1}{3\times7}\) + \(\dfrac{1}{7\times11}\)+\(\dfrac{1}{11\times15}\)+...+\(\dfrac{1}{a\times\left(a+4\right)}\) = \(\dfrac{49}{597}\)

(\(\dfrac{1}{3\times7}\)+ \(\dfrac{1}{7\times11}\)+\(\dfrac{1}{11\times15}\)+...+\(\dfrac{1}{a\times\left(a+4\right)}\))\(\times\)4 = \(\dfrac{49}{597}\)\(\times\) 4

\(\dfrac{4}{3\times7}\)+\(\dfrac{4}{7\times11}\)+\(\dfrac{4}{11\times15}\)+...+\(\dfrac{4}{a\times\left(a+4\right)}\) = \(\dfrac{196}{597}\)

\(\dfrac{1}{3}\) - \(\dfrac{1}{7}\) + \(\dfrac{1}{7}\) - \(\dfrac{1}{11}\) + \(\dfrac{1}{11}\)- \(\dfrac{1}{15}\)+...+ \(\dfrac{1}{a}-\dfrac{1}{a+4}\) = \(\dfrac{196}{597}\)

\(\dfrac{1}{3}\) - \(\dfrac{1}{a+4}\) = \(\dfrac{196}{597}\)

       \(\dfrac{1}{a+4}\) =\(\dfrac{1}{3}-\) \(\dfrac{196}{597}\)

       \(\dfrac{1}{a+4}\) = \(\dfrac{1}{199}\)

       \(a\) + 4 = 199

      \(a\)        = 199 - 4

      \(a\)       = 195 

X = {5; 7; 9; 11; 13;...;83}

Xét dãy số: 5; 7; 9;11; 13;...; 83

Dãy số trên là dãy số cách đều có khoảng cách là: 7 - 5 = 2

Phần tử thứ 11 của tập hợp X chính là số hạng thứ 11 của dãy số trên

Áp dụng công thức tính số thứ n của dãy số cách đều: 

St_n = số đầu + khoảng cách \(\times\)(n-1)

Số thứ 11 của dãy số trên là: 5 + 2 \(\times\) ( 11 - 1) = 25

Kết luận:

Phần tử đứng thứ 11 tính từ trái qua phải của tập hợp X khi các phần tử của tập hợp X được sắp xếp theo thứ tự từ bé đến lớn là: 25

\(\dfrac{1}{3\times7}+\dfrac{1}{7\times11}+\dfrac{1}{11\times15}+...+\dfrac{1}{a\times\left(a+4\right)}=\dfrac{50}{609}\)

\(\dfrac{1}{4}\times\left(\dfrac{4}{3\times7}+\dfrac{4}{7\times11}+...+\dfrac{4}{a\times\left(a+4\right)}\right)=\dfrac{50}{609}\)

\(\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+...+\dfrac{1}{a}-\dfrac{1}{a\times4}=\dfrac{50}{609}\div\dfrac{1}{4}\)

\(\dfrac{1}{3}-\dfrac{1}{a\times4}=\dfrac{200}{609}\)

\(\dfrac{1}{a\times4}=\dfrac{1}{3}-\dfrac{200}{609}\)

\(\dfrac{1}{a\times4}=\dfrac{1}{203}\)

\(a\times4=203\)

\(a=\dfrac{203}{4}\)

 \(\dfrac{1}{3\times7}\)+\(\dfrac{1}{7\times11}\)+\(\dfrac{1}{11\times15}\)+...+\(\dfrac{1}{a\times\left(a+4\right)}\)  = \(\dfrac{50}{609}\)

 4\(\times\)( \(\dfrac{1}{3\times7}\) +\(\dfrac{1}{7\times11}\)+\(\dfrac{1}{11\times15}\)+...+\(\dfrac{1}{a\times\left(a+4\right)}\)) = \(\dfrac{50}{609}\) \(\times\)4

\(\dfrac{4}{3\times7}\)+ \(\dfrac{4}{7\times11}\)+\(\dfrac{1}{11\times15}\)+...+\(\dfrac{4}{a\times\left(a+4\right)}\) = \(\dfrac{50}{609}\) \(\times\) 4

\(\dfrac{1}{3}\) - \(\dfrac{1}{7}\) + \(\dfrac{1}{7}\) - \(\dfrac{1}{11}\) + \(\dfrac{1}{11}\)-\(\dfrac{1}{15}\)+...+\(\dfrac{1}{a}\)-\(\dfrac{1}{a+4}\) = \(\dfrac{200}{609}\)

\(\dfrac{1}{3}\) - \(\dfrac{1}{a+4}\) = \(\dfrac{200}{609}\)

         \(\dfrac{1}{a+4}\) = \(\dfrac{1}{3}\) - \(\dfrac{200}{609}\)

           \(\dfrac{1}{a+4}\) = \(\dfrac{1}{203}\)

             a + 4  = 203

                 \(a\) = 203 - 4

                 \(a\) = 199

Đáp số: \(a\) = 199