tìm đặc điểm , ý kiến , lí lẽ , bằng chứng trong tác phẩm :"Hai vạn dặm dưới đáy biển"
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cấu hình X: 1s22s22p1
=> X có 5e => STT ô thứ 5, chu kì 2, nhóm IIIA

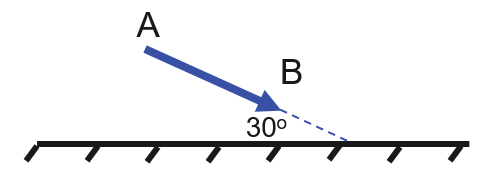
a. Ảnh của vật sáng tạo bởi gương phẳng được vẽ đối xứng với vật qua gương phẳng.
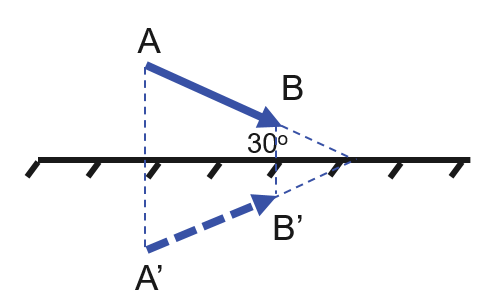
Tính chất của ảnh tạo bởi gương phẳng:
- Ảnh ảo, không hứng được trên màn
- Độ lớn ảnh bằng độ lớn vật
- Khoảng cách từ một điểm của vật đến gương phẳng bằng khoảng cách từ ảnh của điểm đó đến gương
a. Ảnh của vật sáng tạo bởi gương phẳng được vẽ đối xứng với vật qua gương phẳng.

Tính chất của ảnh tạo bởi gương phẳng:
- Ảnh ảo, không hứng được trên màn
- Độ lớn ảnh bằng độ lớn vật
- Khoảng cách từ một điểm của vật đến gương phẳng bằng khoảng cách từ ảnh của điểm đó đến gương

Tốc độ khi lên dốc:
v1=v22=602=30v1=2v2=260=30 km/h
Tốc độ khi xuống dốc:
v3=1,5v2=1,5.60=90v3=1,5v2=1,5.60=90 km/h
Độ dài cung đường trên là:
�=�1+�2+�3=v1�1+v2�2+v3�3=30.12+60.16+90.16=40s=s1+s2+s3=v1t1+v2t2+v3t3=30.21+60.61+90.61=40 km
t1 = 30 min = 1/2 h ; v1=v22v1=2v2
v2v2 = 60 km/h ; �2t2 = 10 min = 1661 h
�3t3 = 10 min = 1661 h ; v3=1,5v2v3=1,5v2
�s = ? (km)
Giải:
Tốc độ khi lên dốc:
v1=v22=602=30v1=2v2=260=30 km/h
Tốc độ khi xuống dốc:
v3=1,5v2=1,5.60=90v3=1,5v2=1,5.60=90 km/h
Độ dài cung đường trên là:
�=�1+�2+�3=v1�1+v2�2+v3�3=30.12+60.16+90.16=40s=s1+s2+s3=v1t1+v2t2+v3t3=30.21+60.61+90.61=40 km

Lời giải:
a. Ta thấy: $AB\perp BC, CD\perp BC$
$\Rightarrow AB\parallel CD$
$BC\perp CD; DE\perp CD$
$\Rightarrow BC\parallel DE$
b.$AB\perp BC, BC\parallel DE\Rightarrow AB\perp DE$
Mà $DE\perp EF$
$\Rightarrow AB\parallel EF$
c.
Do $AB\parallel CD$ nên:
$\widehat{AIC}+\widehat{IAB}=180^0$ (2 góc trong cùng phía)
$\Rightarrow \widehat{AIC}=180^0-\widehat{IAB}=180^0-50^0=130^0$

a) C/m tam giác BAD = tam giác BED
xét tam giác BAD và tam giác BED, ta có
BD chung
BA = BE (gt)
ABD = DBE (BD tia phân giác góc ABC)
=>tam giác BAD = tam giác BED
=>AD=DE( cặp cạnh tương ứng)
b) chứng minh AF = EC
Xét tam giác ADF và tam giác EDC, ta có
AD = DE( cmt )
ADF = EDC( đối đỉnh )
DAF=DEC( = 900)
=>tam giác ADF = tam giác EDC
=>AF = EC ( cặp cạnh tương ứng)
=>ECA=AFE(cặp góc tương ứng )
c) C/M AE // FC
tam giác BEC có
BE = BA ( gt )
=> tam giác BEC cân cại B
=>BEA=BAE
ta có
ED = AD
DF = DC
=>ED+DF=AD+DC
=>EF=AC
xét tam giác ACF và tam giác EFC, ta có
EC = AF (cmt)
CF chung
EF=AC(cmt)
=>tam giác ACF= tam giác EFC
=>EFC=ACF(cặp góc tương ứng)
ta có:
ECA = AFE(cmt)
ACF=EFC(cmt)
=>ECA+ACF=AFE+EFC
=>ECF=AFC
tam giác BCF có
BCF=BFC(cmt)
=>tam giác BCF cân tại B
Ta có
tam giác BEC cân tại B
tam giác BCF cân tại B
=>BEA=BCF=BAE=BFC
mà BEA đồng vị BCF
=> AE//FC
cái câu c mình ko chắc đúng lắm nha.('v')

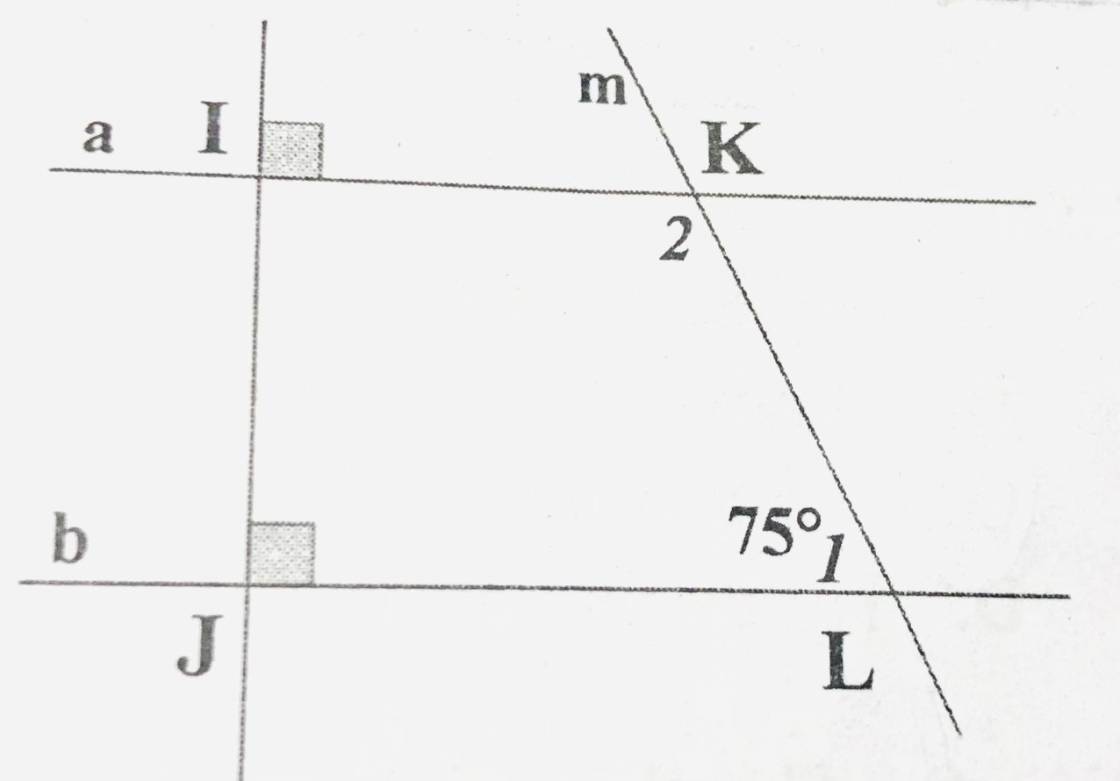
a \(\perp\) IJ
b \(\perp\) IJ
⇒ a//b (Vì trong cùng một mặt phẳng hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
\({}\)\(\widehat{K_2}\) + \(\widehat{L_1}\)= 1800 (hai góc trong cùng phía có tổng bằng 1800)
\({}\) \(\widehat{K_2}\) = 1800 - 750
\({}\) \(\widehat{K_2}\) = 1050