https://sachdientutienganh.com/i-learn-smart-start-grade-4-sb/

Để giải quyết bài toán ngày sinh nhật của Cheryl, hãy xem xét các thông tin đã được tiết lộ và áp dụng quy luật loại trừ:

1. Cheryl đưa ra 10 ngày mà ngày sinh nhật có thể rơi vào: 15/5, 16/5, 19/5, 17/6, 18/6, 14/7, 16/7, 14/8, 15/8 và 17/8.

2. Albert biết rằng Bernard không biết ngày sinh nhật của Cheryl. Điều này cho biết ngày sinh không nằm trong các ngày 14 và 15, vì nếu Cheryl sinh vào ngày 14 hoặc 15, Bernard sẽ biết ngày sinh của cô.

3. Bernard sau khi nghe Albert nói, biết được ngày sinh của Cheryl. Điều này chỉ ra rằng ngày sinh của Cheryl phải là duy nhất trong tháng mà Bernard được nghe thông tin từ Albert. Điều này loại trừ các ngày 14 và 17, vì nếu Cheryl sinh vào ngày 14 hoặc 17, Bernard không thể biết ngày sinh của cô.

4. Albert sau khi nghe Bernard nói, cũng biết ngày sinh của Cheryl. Vì Albert biết rằng Bernard đã loại bỏ các ngày 14 và 17, và Albert cũng biết rằng Bernard đã biết ngày sinh của Cheryl sau khi nghe thông tin từ mình. Do đó, ngày sinh của Cheryl không thể là 16, vì nếu Cheryl sinh vào ngày 16, Bernard vẫn còn nhiều khả năng nghĩ rằng ngày sinh của cô là ngày 14 hoặc 17.

Dựa vào những thông tin trên, ngày sinh của Cheryl là ngày 19/5.

Vì cậu thích :/

Để giải quyết bài toán ngày sinh nhật của Cheryl, hãy xem xét các thông tin đã được tiết lộ và áp dụng quy luật loại trừ:

1. Cheryl đưa ra 10 ngày mà ngày sinh nhật có thể rơi vào: 15/5, 16/5, 19/5, 17/6, 18/6, 14/7, 16/7, 14/8, 15/8 và 17/8.

2. Albert biết rằng Bernard không biết ngày sinh nhật của Cheryl. Điều này cho biết ngày sinh không nằm trong các ngày 14 và 15, vì nếu Cheryl sinh vào ngày 14 hoặc 15, Bernard sẽ biết ngày sinh của cô.

3. Bernard sau khi nghe Albert nói, biết được ngày sinh của Cheryl. Điều này chỉ ra rằng ngày sinh của Cheryl phải là duy nhất trong tháng mà Bernard được nghe thông tin từ Albert. Điều này loại trừ các ngày 14 và 17, vì nếu Cheryl sinh vào ngày 14 hoặc 17, Bernard không thể biết ngày sinh của cô.

4. Albert sau khi nghe Bernard nói, cũng biết ngày sinh của Cheryl. Vì Albert biết rằng Bernard đã loại bỏ các ngày 14 và 17, và Albert cũng biết rằng Bernard đã biết ngày sinh của Cheryl sau khi nghe thông tin từ mình. Do đó, ngày sinh của Cheryl không thể là 16, vì nếu Cheryl sinh vào ngày 16, Bernard vẫn còn nhiều khả năng nghĩ rằng ngày sinh của cô là ngày 14 hoặc 17.

Dựa vào những thông tin trên, ngày sinh của Cheryl là ngày 19/5.

Ta có biểu thức: \(2023\times\left(10-a\right)\)

Có giá trị bé nhất khi \(10-a\) phải bé nhất 

Mà \(10-a\) bé nhất thì phải bằng 1 

Ta có: \(10-a=1\)

Vậy: \(a=9\) thì biểu thức sẽ có giá trị nhỏ nhất.

2023 *(10-9)

Câu 1: Sắp xếp theo thứ tự từ bé đến lớn: \(\dfrac{3}{10};\dfrac{1}{2};\dfrac{18}{19};\dfrac{19}{20}\)

Câu 2: \(\dfrac{3}{4}+\left(2\times y-1\right)=\dfrac{5}{6}\)

\(2\times y-1=\dfrac{5}{6}-\dfrac{3}{4}\)

\(2\times y=\dfrac{1}{12}+1\)

\(y=\dfrac{13}{12}:2=\dfrac{13}{24}\)

Câu 3: Số có hai chữ số nhỏ nhất là

Số có hai chữ số lớn nhất là 

Vậy: Phân số cần tìm là  

Câu 4: 6 năm nữa tuổi mẹ sẽ gấp 3 lần tuổi con

Câu 5: Các phân số là: \(\dfrac{1}{8};\dfrac{2}{7};\dfrac{3}{6};\dfrac{4}{5};\dfrac{5}{4};\dfrac{6}{3};\dfrac{7}{2};\dfrac{8}{1}\)

Câu 6: \(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}\)

\(=\dfrac{1}{1\times2}+\dfrac{1}{2\times3}+\dfrac{1}{3\times4}+\dfrac{1}{4\times5}+\dfrac{1}{5\times6}+\dfrac{1}{6\times7}\)

\(=\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}\)

\(=\dfrac{1}{1}-\dfrac{1}{7}=\dfrac{6}{7}\)

À mình nhầm 1 chút. Tích \(P=\left(1+1\right)\left(2+1\right)\left(3+1\right)...\left(2023+1\right)\) và do đó nếu \(a_0\) là số cuối cùng trên bảng thì\(\dfrac{1}{a_0}+1=\left(1+1\right)\left(2+1\right)\left(3+1\right)...\left(2023+1\right)\) hay \(a_0=\dfrac{1}{2.3.4...2024-1}\). Vậy số cuối cùng là \(\dfrac{1}{2.3.4...2024-1}\)

 Nếu trên bảng có các số \(a_1,a_2,...,a_n\) thì ta xét tích \(P=\left(\dfrac{1}{a_1}+1\right)\left(\dfrac{1}{a_2}+1\right)...\left(\dfrac{1}{a_n}+1\right)\). Sau mỗi bước, ta thay 2 số \(a_i,a_j\) bằng số \(a_k=\dfrac{a_ia_j}{a_i+a_j+1}\). Khi đó \(\dfrac{1}{a_k}+1=\dfrac{a_i+a_j+1}{a_ia_j}+1=\dfrac{1}{a_i}+\dfrac{1}{a_j}+\dfrac{1}{a_ia_j}+1\) \(=\dfrac{1}{a_j}\left(\dfrac{1}{a_i}+1\right)+\left(\dfrac{1}{a_i}+1\right)\) \(=\left(\dfrac{1}{a_i}+1\right)\left(\dfrac{1}{a_j}+1\right)\)

 Như vậy, sau phép biến đổi ban đầu, tích\(P=\left(\dfrac{1}{a_1}+1\right)\left(\dfrac{1}{a_2}+1\right)...\left(\dfrac{1}{a_k}+1\right)...\left(\dfrac{1}{a_n}+1\right)\)

\(P=\left(\dfrac{1}{a_1}+1\right)\left(\dfrac{1}{a_2}+1\right)...\left(\dfrac{1}{a_i}+1\right)\left(\dfrac{1}{a_j}+1\right)...\left(\dfrac{1}{a_n}+1\right)\)

 Là không thay đổi. Vì vậy, số cuối cùng còn lại trên bảng chính là giá trị của tích P. Lại có 

\(P=\left(1+1\right)\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}+1\right)...\left(\dfrac{1}{2023}+1\right)\)

\(P=2.\dfrac{3}{2}.\dfrac{4}{3}...\dfrac{2024}{2023}=2024\)

Như vậy, số cuối cùng trên bảng sẽ bằng 2024.

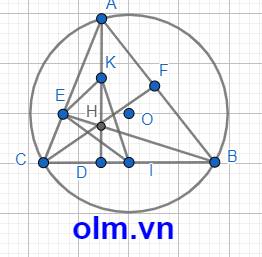
a, Xét tam giác vuông EBC vuông tại E và  CI = IB

 ⇒ IE = IC = IB ⁽¹⁾ ( vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)

Xét tam giác vuông BCF vuông tại F và IC =IB 

 ⇒IF = IC = IB ⁽²⁾ (vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền) 

Từ (1) và (2) ta có: 

IE = IF = IB = IC 

Vậy bốn điểm B, C, E, F cùng thuộc một đường tròn tâm I bán kính bằng \(\dfrac{1}{2}\) BC (đpcm)

b, Xét \(\Delta\)AFC và \(\Delta\)AEB có:

\(\widehat{CAF}\)  chung ; \(\widehat{AFC}\) = \(\widehat{AEB}\) = 90⁰ 

⇒ \(\Delta\)AFC  \(\sim\) \(\Delta\)AEB   (g-g)

⇒ \(\dfrac{AF}{AE}\) = \(\dfrac{AC}{AB}\) (theo định nghĩa hai tam giác đồng dạng)

⇒AB.AF = AC.AE (đpcm)

Xét tam giác vuông AEH vuông tại E và KA = KH 

⇒ KE = KH ( vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)

⇒\(\Delta\)EKH cân tại K ⇒ \(\widehat{KEH}\) = \(\widehat{EHK}\) 

\(\widehat{EHK}\) = \(\widehat{DHB}\) (vì hai góc đối đỉnh)

 ⇒ \(\widehat{KEH}\) = \(\widehat{DHB}\) ( tc bắc cầu) (3)

Theo (1) ta có: IE = IB ⇒ \(\Delta\) IEB cân tại I 

⇒ \(\widehat{IEB}\) = \(\widehat{IBE}\)  (4)

Cộng vế với vế của (3) và(4)

Ta có: \(\widehat{KEI}\) = \(\widehat{KEH}\) + \(\widehat{IEB}\) =  \(\widehat{DHB}\) + \(\widehat{IBE}\)  = \(\widehat{DHB}\) + \(\widehat{DBH}\)

        Vì tam giác DHB vuông tại D nên \(\widehat{DHB}\) + \(\widehat{DBH}\)  = 180⁰ - 90⁰ = 90⁰

 ⇒\(\widehat{KEI}\)  = 90⁰

         IE \(\perp\) KE (đpcm)

help

s0s

Đây là dạng nâng cao toán tổng hiệu, trong các kỳ thi hsg thi violympic, mà hiệu đang bị ẩn em nhé

Bước 1:  Em tìm hiệu hai số (bằng sơ đồ đoạn thẳng)

Bước 2: Em giải toán tổng hiệu bình thường.

Theo sơ đồ ta có hiệu hai số là: 2 \(\times\) (7-1) + 2 = 14

Ta có sơ đồ:

Theo sơ đồ ta có: Số chẵn lớn là: (398 +14):2  = 206

Đáp số: 206 

Đặt hai số chẵn đó là x và y, với x là số chẵn lớn hơn. Ta có các điều kiện sau:

1. x + y = 398 (tổng hai số chẵn bằng 398)
2. x - y = 2 × 7 = 14 (số lẻ giữa hai số chẵn)

Giải hệ phương trình này để tìm giá trị của x và y:

Thêm cả hai phương trình lại với nhau, ta có: (x + y) + (x - y) = 398 + 14 2x = 412 x = 412 / 2 x = 206

Thay x vào phương trình thứ nhất, ta có: 206 + y = 398 y = 398 - 206 y = 192

Vậy, số chẵn lớn hơn trong hai số đó là 206.

Thời gian từ nửa đêm đến giờ cũng chính là thời gian bây giờ

Theo bài ra ta có: 

2 lần thời gian từ bây giờ đến giữa trưa cùng ngày bằng:

1 -  \(\dfrac{1}{7}\) = \(\dfrac{6}{7}\) (thời gian bây giờ)

Tỉ số thời gian từ bây giờ đến giữa trưa cùng ngày và thời gian bây giờ là:

\(\dfrac{6}{7}\) : 2 = \(\dfrac{3}{7}\)

Tổng thời gian bây giờ và thời gian từ giờ đến giữa trưa cùng ngày là 24 : 2 = 12(giờ)

Ta có sơ đồ:

Theo sơ đồ ta có: 

Thời gian bây giờ là: 12: (3+7) \(\times\) 7 = 8,4 (giờ)

Đổi 8,4 giờ = 8 giờ 24 phút

Đáp số: 8 giờ 24 phút