no ,không được đâu 

Bài 1: 

Kẻ \(OM\perp AB\), \(OM\)cắt \(CD\)tại \(N\).

Khi đó \(MN=8cm\).

TH1: \(AB,CD\)nằm cùng phía đối với \(O\).

\(R^2=OC^2=ON^2+CN^2=h^2+\left(\frac{25}{2}\right)^2\)(\(h=CN\)) (1)

\(R^2=OA^2=OM^2+AM^2=\left(h+8\right)^2+\left(\frac{15}{2}\right)^2\)(2) 

Từ (1) và (2) suy ra \(R=\frac{\sqrt{2581}}{4},h=\frac{9}{4}\).

TH2: \(AB,CD\)nằm khác phía với \(O\).

\(R^2=OC^2=ON^2+CN^2=h^2+\left(\frac{25}{2}\right)^2\)(\(h=CN\)) (3)

\(R^2=OA^2=OM^2+AM^2=\left(8-h\right)^2+\left(\frac{15}{2}\right)^2\)(4)

Từ (3) và (4) suy ra \(R=\frac{\sqrt{2581}}{4},h=\frac{-9}{4}\)(loại).

Bài 3: 

Lấy \(A'\)đối xứng với \(A\)qua \(Ox\), khi đó \(A'\)có tọa độ là \(\left(1,-2\right)\).

\(MA+MB=MA'+MB\ge A'B\)

Dấu \(=\)xảy ra khi \(M\)là giao điểm của \(A'B\)với trục \(Ox\).

Suy ra \(M\left(\frac{5}{3},0\right)\).

a/ Áp dụng BĐT Cô-si cho các số dương ta được

abc+bca≥2√abc.bca=2cabc+bca≥2abc.bca=2c

Tương tự

abc+cab≥2babc+cab≥2b

bca+cab≥2abca+cab≥2a

Cộng các vế của BĐT

2(abc+bca+cab)≥2(1a+1b+1c)2(abc+bca+cab)≥2(1a+1b+1c)

↔abc+bca+cab≥1a+1b+1c↔abc+bca+cab≥1a+1b+1c

b/ Áp dụng BĐT Cô-si cho các số dương ta được

abc+bca≥2√abc.bca=2babc+bca≥2abc.bca=2b

Tương tự

abc+cab≥2aabc+cab≥2a

bca+cab≥2cbca+cab≥2c

Cộng các vế của BĐT

2(abc+bca+cab)≥2(a+b+c)2(abc+bca+cab)≥2(a+b+c)

↔abc+bca+cab≥a+b+c

MIK KO BT

( -----------------) 

KO BT

Số nhị phân

@Bảo

#Cafe

so nhi phan

hok tot

hi

mình mới lớp 6 nên kc bt xin lỗi à

Bài 2:

a) Với m ≠ 0, phương trình trên là phương trình bậc hai ẩn x

Δ' = (m + 1)2 - m(m - 4) = m2 + 2m + 1 - m2 + 4m = 6m + 1

Phương trình có 2 nghiệm x1; x2 khi và chỉ khi Δ' = 6m + 1 ≥ 0

Khi đó, theo định lí Vi-et ta có:

Theo bài ra:

x1 + 4x2 = 3

<=> (x1 + x2 ) + 3x2 = 3

 + 3x2 = 3

=> 5m2 - 2m - 16 = 9m2 - 36m

<=> 4m2 - 34m + 16 = 0

Đối chiếu với điều kiện thỏa mãn

Vậy m = 8, m =  thì x1 + 4x2 = 3

b) Ta có:

2(x1 + x2 ) + x1x2 =  = 5

Vậy hệ thức liên hệ giữa x1 và x2 không phụ thuộc vào m là 2(x1 + x2 ) + x1x2 = 5

Bài 3:

Gọi số học sinh lớp 9A là x ( học sinh) (x > 8, x ∈ N)

Khi đó, số cây mỗi học sinh phải trồng là:

 (cây học sinh )

Do có 8 bạn học sinh vắng mặt nên số cây mỗi bạn phải trồng là

 (cây học sinh )

Theo bài ra, mỗi bạn phải trồng thêm 3 cây nên ta có phương trình

=> 480(x - 8) + 3x(x - 8) = 480x

<=> 3x2 - 24x - 3840 = 0

Vậy số học sinh lớp 9A là 40 học sinh

Bài 4:

a) Xét tứ giác AMHN có:

∠AMH = 90o (MH ⊥ AB)

∠ANH = 90o (NH ⊥ AC)

=> ∠AMH + ∠ANH = 180o

=> Tứ giác AMHN là tứ giác nội tiếp

b) Ta có:

ΔAMH vuông tại M: ∠AHM + ∠MAH = 90o

ΔABH vuông tại H: ∠ABC + ∠MAH = 90o

=> ∠AHM = ∠ABC

Do tứ giác AMHN là tứ giác nội tiếp nên ∠AHM = ∠ANM (2 góc nội tiếp cùng chắn cung AM)

=> ∠ABC = ∠ANM

c) Kẻ đường kính AD của (O), Gọi I là giao điểm của AD và MN

ΔANH vuông tại N: ∠AHN + ∠NAH = 90o

ΔACH vuông tại H: ∠AHN + ∠ACB = 90o

=> ∠NAH = ∠ACB

Ta lại có: ∠ACB = ∠ADB (2 góc nội tiếp cùng chắn cung AB)

=> ∠NAH = ∠ADB

Mặt khác: tứ giác AMHN là tứ giác nội tiếp nên ∠AMN = ∠AHN (2 góc nội tiếp cùng chắn cung AN)

=> ∠AMN = ∠ADB

Xét ΔAMI và ΔABD có:

∠BAD là góc chung

∠AMN = ∠ADB

=> ΔAMI ∼ ΔADB

=> ∠ AIM = ∠ABD

Mà ∠ABD = 90o (góc nội tiếp chắn nửa đường tròn)

=> ∠AIM = 90o

Hay OA ⊥ MN

d) Xét tam giác AIN và tam giác ACD có:

∠DAC là góc chung

∠AIN = ∠ACD = 90o

=> ΔAIN ∼ ΔACD

=><=> AI.AD = AC.AN (1)

Xét ΔAHC vuông tại H có HN là đường cao

=> AC. AN = AH2 (2)

Từ (1) và (2) => AI.AD = AH2 <=> AI.AD = 2R2

<=> AI.2R = 2R2 <=> AI = R <=> I ≡ O

Vậy M, N, O thẳng hàng.

Bài 5:

Do a, b > 0 nên ta có:

Dấu bằng xảy ra khi:

Vậy GTLN của P là 2√2, đạt được khi a = b = 1.

em muốn giải lắm nhưng lại là lớp 5

Giải thích các bước giải:

M Al₂O₃.SiO₂.2H₂O = 198 

%m_Al = = 27.2.100:198= 27,27%

48 % nhé bạn

uầy hello người AE bản sao : bài này :

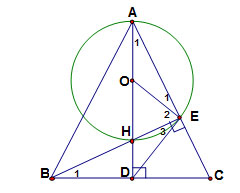
1. Xét tứ giác CEHD ta có:

góc CEH = 90⁰ (Vì BE là đường cao)

góc CDH = 90⁰ (Vì AD là đường cao)

=> góc CEH + góc CDH = 180⁰

Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp

2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEA = 90⁰.

AD là đường cao => AD ┴ BC => BDA = 90⁰.

Như vậy E và D cùng nhìn AB dưới một góc 90⁰ => E và D cùng nằm trên đường tròn đường kính AB.

Vậy bốn điểm A, E, D, B cùng nằm trên một đường tròn.

TL
 

Bn tham khảo

1. Xét tứ giác CEHD ta có:

góc CEH = 90⁰ (Vì BE là đường cao)

góc CDH = 90⁰ (Vì AD là đường cao)

=> góc CEH + góc CDH = 180⁰

Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp

2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEA = 90⁰.

AD là đường cao => AD ┴ BC => BDA = 90⁰.

Như vậy E và D cùng nhìn AB dưới một góc 90⁰ => E và D cùng nằm trên đường tròn đường kính AB.

Vậy bốn điểm A, E, D, B cùng nằm trên một đường tròn.

3. Theo giả thiết tam giác ABC cân tại A có AD là đường cao nên cũng là đường trung tuyến

=> D là trung điểm của BC. Theo trên ta có góc BEC = 90⁰.

Vậy tam giác BEC vuông tại E có ED là trung tuyến => DE = 1/2 BC.

4. Vì O là tâm đường tròn ngoại tiếp tam giác AHE nên O là trung điểm của AH => OA = OE => tam giác AOE cân tại O => góc E₁ = góc A₁ (1).

Theo trên DE = 1/2 BC => tam giác DBE cân tại D => góc E₃ = góc B₁ (2)

Mà góc B₁ = góc A₁ (vì cùng phụ với góc ACB) => góc E₁ = góc E₃ => góc E₁ + góc E₂ = góc E₂ + góc E₃

Mà góc E₁ + góc E₂ = góc BEA = 90⁰ => góc E₂ + góc E₃ = 90⁰ = góc OED => DE ┴ OE tại E.

Vậy DE là tiếp tuyến của đường tròn (O) tại E.

5. Theo giả thiết AH = 6 Cm => OH = OE = 3 cm.; DH = 2 Cm => OD = 5 cm. Áp dụng định lí Pitago cho tam giác OED vuông tại E ta có ED² = OD² – OE² ↔ ED² = 5² – 3² ↔ ED=4cm

Hok tốt