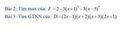
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


hỏi bài nhìu vậy, cứ thử suy nghĩ đi, một vài câu nào ko làm đc thì hỏi


Xét hình bình hành \(ABCD\).
\(\overrightarrow{a}=\overrightarrow{AB},\overrightarrow{b}=\overrightarrow{AD}\)
\(\left|\overrightarrow{a}\right|-\left|\overrightarrow{b}\right|=AB-AD=AB-DC\)
\(\left|\overrightarrow{a}+\overrightarrow{b}\right|=\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=\left|\overrightarrow{AC}\right|=AC\)
\(\left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|=AB+AD=AB+CD\).
Xét tam giác \(ADC\)có:
\(AB-DC< AC< AB+DC\)(theo bất đẳng thức tam giác)
Do đó ta suy ra đpcm.

Xin lỗi chị, em ko biết làm em mới lớp 6 thooy ạ. Nhưng em rất muốn đc 1 k nhưng lại ko biết làm ạ. Huhu T^T
#Army


 Giúp mình với ạ
Giúp mình với ạ




Bài 2.
\(F=2-3\left[\left(x+1\right)^4+\left(x-5\right)^4\right]\)
Ta có bất đẳng thức phụ:
\(a^4+b^4\ge\frac{1}{8}\left(a+b\right)^4\)
Chứng minh:
\(8\left(a^4+b^4\right)\ge4\left(a^2+b^2\right)^2=\left[2\left(a^2+b^2\right)\right]^2\ge\left(a+b\right)^4\)
(vì \(2\left(x^2+y^2\right)\ge\left(x+y\right)^2\))
Dấu \(=\)khi \(a=b\).
Áp dụng ta có:
\(\left(x+1\right)^4+\left(5-x\right)^4\ge\frac{1}{8}\left(x+1+5-x\right)^4=\frac{1}{8}.6^4=162\).
\(F\le2-3.162=-484\)
Dấu \(=\)khi \(x+1=5-x\Leftrightarrow x=2\).
Bài 3.
\(D=\left(2x-1\right)\left(x+2\right)\left(x+3\right)\left(2x+1\right)\)
\(=\left[\left(2x-1\right)\left(x+3\right)\right]\left[\left(x+2\right)\left(2x+1\right)\right]\)
\(=\left(2x^2+5x-3\right)\left(2x^2+5x+2\right)\)
\(=\left(2x^2+5x-\frac{1}{2}\right)^2-\left(\frac{5}{2}\right)^2\ge-\left(\frac{5}{2}\right)^2=-\frac{25}{4}\)
Dấu \(=\)khi \(2x^2+5x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{4}\left(-5\pm\sqrt{29}\right)\).