Dấu hiệu nhận biết: every morning

Loại câu: Mệnh lệch.

`@` `\text {Ans}`

`\downarrow`

`a,`

`x \times 274 - 256 \times x = 5130`

`x \times (274 - 256) = 5130`

`x \times 18 = 5130`

`x = 5130 \div 18`

`x = 285`

Vậy, `x = 285`

`b,`

`x \times 18 \times 19 = 43434`

`x \times 342 = 43434`

`x = 43434 \div 342`

`x = 127`

Vậy, `x = 127.`

spelling

spelling nha bạn

fly

Fly

how

How this Mai?Fine thanks.

Nửa chu vi bằng: 12 : 2 = 6 (lần chiều rộng hình chữ nhật )

Chiều rộng hình chữ nhât bằng: 1: (6-1) = \(\dfrac{1}{5}\) (chiều dài)

Ta có sơ đồ:

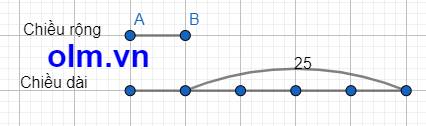
Theo sơ đồ ta có:

Chiều rộng của hình chữ nhật là: 25:(5-1) = \(\dfrac{25}{4}\) (m)

Chiều dài của hình chữ nhật là: 25 + \(\dfrac{25}{4}\) = \(\dfrac{125}{4}\) (m)

Đáp số: chiều dài của hình chữ nhật là \(\dfrac{125}{4}\) m

            chiều rộng của hình chữ nhật là \(\dfrac{25}{4}\) (m)

Lời giải:

Chu vi gấp 12 lần chiều rộng 

$\Rightarrow$ tổng chiều dài và chiều rộng gấp 12:2=6 lần chiều rộng 

Coi chiều rộng là 1 phần thì tổng chiều dài và chiều rộng là 6 phần

Khi đó chiều dài là 6-1=5 phần 

Hiệu chiều dài và chiều rộng là 5-1=4 phần 

Chiều rộng là: $25:4\times 1=6,25$ (m) 

Chiều dài là: $25:4\times 5=31,25$ (m)

why

Why

Số có 3 chữ số có dạng: \(\overline{abc}\)

\(a\) có 3 cách chọn

\(b\) có 3 cách chọn

\(c\) có 2 cách chọn

Số các số có 3 chữ số khác nhau được lập từ các chữ số: 0; 1; 2; 5 là:

                  3 \(\times\) 3 \(\times\) 2 = 18 (số)

Đáp số: 18 số

Lời giải:
Vì $x+1, y+2013$ chia hết cho $6$ nên đặt $x+1=6k, y+2013=6m$ với $k,m\in\mathbb{N}^*$ 

Khi đó:

$4^{x}+x+y=4^{6k-1}+6k-1+6m-2013$

$=4^{6k-1}-2014+6(k+m)$

Vì $4\equiv 1\pmod 3$

$\Rightarrow 4^{6k-1}\equiv 1^{6k-1}\equiv 1\pmod 3$

$\Rightarrow 4^{6k-1}-2014\equiv 1-2014\equiv -2013\equiv 0\pmod 3$

$\Rightarrow 4^{6k-1}-2014\vdots 3$

Mà $4^{6k-1}-2014$ chẵn với mọi $k\in\mathbb{N}^*$

$\Rightarrow 4^{6k-1}-2014\vdots 6$

Kết hợp với $6k+6m\vdots 6$

$\Rightarrow 4^x+x+y=4^{6k-1}-2014+6k+6m\vdots 6$ (đpcm) 

Bài 3:

a, (\(x\)+y+z)²

=((\(x\)+y) +z)²

= (\(x\) + y)² + 2(\(x\) + y)z + z²

= \(x^2\) + 2\(xy\) + y² + 2\(xz\) + 2yz + z²

=\(x^2\) + y² + z² + 2\(xy\) + 2\(xz\) + 2yz

b, (\(x-y\))(\(x^2\) + y² + z² - \(xy\) - yz - \(xz\))

= \(x^3\) + \(xy^2\) + \(xz^2\) - \(x^2\)y - \(xyz\) - \(x^2\)z - y³ 

Đến dây ta thấy xuất hiện \(x^3\) - y³ khác với đề bài, em xem lại đề bài nhé