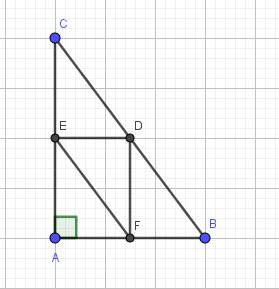
​

a, Xét tứ AHCE ta có: IH = IE ; IA = IC 

⇒ tứ giácAHCE là hình bình hành (1)

Mà AH \(\perp\)  BC \(\equiv\)  H nên ⇒ \(\widehat{AHC}\) = 90⁰ (2)

Kết hợp (1) và (2) ta có: Tứ giác AHCE là hình chữ nhật (đpcm).

b, Xét tam giác AHC có: M là trung  điểm HC; I là trung điểm AC

⇒ AM; HI lần lượt là trung tuyến của tam  giác AHC

⇒ G là trọng tâm của tam giác AHC ⇒ HG = \(\dfrac{2}{3}\)HI ⁽³⁾

IG = HI - HG = HI - \(\dfrac{2}{3}\)HI = \(\dfrac{1}{3}\)HI 

Chứng minh tương tự ta có: KE = \(\dfrac{2}{3}\)IE = \(\dfrac{2}{3}\)HI ⁽⁴⁾ ( vì IE = HI)

IK = IE - KE =  IE - \(\dfrac{2}{3}\)IE = \(\dfrac{1}{3}\)IE = \(\dfrac{1}{3}\)HI (vì HI = IE)

GK = IG + IK = \(\dfrac{1}{3}\)HI + \(\dfrac{1}{3}\)HI = \(\dfrac{2}{3}\)HI ⁽⁵⁾  

Kết hợp(3); (4); (5) ta có: HG = GK = KE (đpcm)

a²+b²+c²=(a²+2ac+c²)-2ac+b²=(a+c)²-2b²+b²=(a+b+c)(a-b+c)
mà a²+b²+c² là số nguyên tố và a+b+c>a-b+c nên a-b+c=1
=> a+c=b+1 => a²+2ac+c²=b²+2b+1 => a²+b²=2b+1=2a+2c+1+1
=>a²-2a+1+c²-2c+1=0 => (a-1)²+(c-1)²=0=>a=c=1=>b=1
Vậy (a,b,c) cần tìm là (1,1,1)

A B C H E I M N G K

a/

Ta có

IA=IC (gt)

IH=IE (gt)

=> AHCE là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)

\(AH\perp BC\Rightarrow\widehat{AHC}=90^o\)

=> AHCE là hình chữ nhật (hình bình hành có 1 góc vuông là HCN)

b/

Xét tg AHC có

MH=MC (gt)

IA=IC (gt)

=> G là trong tâm của tg AHC \(\Rightarrow HG=2IG\) (1)

\(\Rightarrow HG+IG=IH=3IG\) (2)

Chứng minh tương tự ta có K là trọng tâm của tg ACE 

\(\Rightarrow KE=2IK\left(3\right)\Rightarrow KE+IK=IE=3IK\) (4)

Mà IH=IE (gt) (5)

Từ (2) (4) (5) => IG=IK (6)

Từ (1) (3) (6) => HG=KE

Mà IG=IK => IG+IKGK=2IK=KE

=> HG=GK=KE

A B C D E F

a/

DE//AB=> DE//AF

DF//AC=>DF//AE

=> AEDF là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)

Hình bình hành AEDF có \(\widehat{A}=90^o\) => AEDF là hình chữ nhật

b/

DE//AB

DB=DC (1)

=> FA=FC (trong tg đường thẳng đi qua trung điểm 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại (2)

Từ (1) và (2) => DE là đường trung bình của ABC

\(\Rightarrow DE=\dfrac{BC}{2}=FB=FC\) (3)

DE//AB=> DE//FB (4)

Từ (3) và (4) => BFED là hình bình hành (Tứ giác có cặp cạnh đối // và bằng nhau là hbh)

a) Do DE // AB (gt)

\(AC\perp AB\) (\(\Delta ABC\) vuông tại A)

\(\Rightarrow DE\perp AC\)

\(\Rightarrow\widehat{DEA}=90^0\)

Do DF // AC (gt)

\(AB\perp AC\) (\(\Delta ABC\) vuông tại A)

\(\Rightarrow DF\perp AC\)

\(\Rightarrow\widehat{DFA}=90^0\)

Tứ giác AEDF có:

\(\widehat{EAF}=\widehat{DEA}=\widehat{DFA}=90^0\)

\(\Rightarrow AEDF\) là hình chữ nhật

b) Do D là trung điểm BC (gt)

DF // AB (gt)

\(\Rightarrow F\) là trung điểm của AB

\(\Rightarrow FA=FB\)

Do AEDF là hình bình hành

\(\Rightarrow DE=AF\)

\(\Rightarrow DE=FB\)

Lại có:

DE // AB

\(\Rightarrow\) DE // FB

Tứ giác BFED có:

DE // FB (cmt)

DE = FB (cmt)

\(\Rightarrow BFED\) là hình bình hành

1. more fluently

2.more happily

3.earlier

4.later

5.more gracefully

6.louder

7.better

8.slower

9.higher

10.farther

11.more carefully

12.more often

13.faster

14.worse

15.harder

Bạn ơi, có lỗi chính tả kìa. Test chứ không phải là Tast với cả câu 7 thiếu từ "than". Còn ở câu 14 thì "I" đứng cuối phải là "Me" nhé

1. I speak English more fluently than last year.

2.They smiled more happily than before.

3. Tom arrived earlier than I expected.

4. We will meet later in this afternoon.

5. Mary dances more gracefully than anyone else.

6.  Could you speak louder?

7. Jim could do test better than Jane

8. We walked more slowly than other people.

9. Planes can fly higher than birds.

10. I can throw the ball farther than anyone else in my team.

11. James drives more carefully than his wife.

12. I visit my grandmother more often than my brother.

13. No one can run faster than John.

14. My sister cooks worse than me.

15. Everyone in company is working harder than ever before.

\(A=\dfrac{2024}{x^2-2x+8}\)

Ta có :

\(x^2-2x+8=x^2-2x+1+7=\left(x-1\right)^2+7\ge7,\forall x\inℝ\)

\(\Rightarrow\dfrac{1}{x^2-2x+8}\le\dfrac{1}{7}\)

\(\Rightarrow A=\dfrac{2024}{x^2-2x+8}\le\dfrac{2024}{7}\)

\(\Rightarrow Max\left(A\right)=\dfrac{2024}{7}\left(tạix=1\right)\)

A B C E K H D M

a/

Ta có

\(\widehat{B}=\widehat{C}\) (góc ở đáy tg cân ABC)

EK//AB \(\Rightarrow\widehat{EKC}=\widehat{B}\) (góc đồng vị)

\(\Rightarrow\widehat{EKC}=\widehat{C}\) => tg EKC cân tại E => CE=EK

Mà AD=CE 

=> AD=EK (1)

Ta có

EK//AB => EK//AD (2)

Từ (1) và (2) => ADKE là hình bình hành (Tứ giác có 1 cặp cạnh đối // và bằng nhau là hbh)

=> MA=MK; MD=ME (Trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)

b/

Ta có \(H\in\left(M;MK\right)\) => MH=MK

Mà MK=MA (cmt) 

=> MH=MK=MA

=> tg MHK cân tại M \(\Rightarrow\widehat{MHK}=\widehat{MKH}\)

\(\widehat{HMK}+\widehat{MHK}+\widehat{MKH}=\widehat{HMK}+2\widehat{MHK}=180^o\)  (tổng các góc trong của 1 tg = 180 độ)

MH=MK=MA (cmt) => tg MAH cân tại M

\(\Rightarrow\widehat{MAH}=\widehat{MHA}\)

\(\widehat{HMK}=\widehat{MAH}+\widehat{MHA}\) (trong tg góc ngoài bằng tổng 2 góc trong không kề với nó)

\(\Rightarrow\widehat{HMK}=2\widehat{MHA}\)

Từ \(\widehat{HMK}+2\widehat{MHK}=180^o\Rightarrow2\widehat{MHA}+2\widehat{MHK}=180^o\)

\(\Rightarrow\widehat{MHA}+\widehat{MHK}=\widehat{AHK}=90^o\Rightarrow AH\perp BC\)

Xét tg vuông ABH và tg vuông ACH có

AH chung

AB=AC (cạnh bên tg cân ABC)

=> tg AHB = tg AHC (Hai tg vuông có cạnh huyền và cạnh góc vuông bằng nhau)

=> HB=HC

Em cảm ơn ạ

6. A.de'test     B.'balance     C.'leisure     D.'muscle

\(\Rightarrow\) Choose A

7. A.pre'fer     B.out'doors     C.re'sort      D.'message

\(\Rightarrow\) Choose D