(x - 5)3 = 64
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


37x - 1 = 36
⇒ 7x - 1 = 6
⇒ 7x = 7
⇒ x = 1.
Vậy x = 1.

a) Ta có: HA = 2RcosA HB = 2RcosB HC = 2RcosC AB = 2RsinC AC = 2RsinB Vậy ta cần chứng minh: 2RcosA + 2RcosB + 2RcosC < 2RsinC + 2RsinB Chia cả 2 vế cho 2R, ta có: cosA + cosB + cosC < sinC + sinB Áp dụng bất đẳng thức tam giác, ta có: sinC + sinB > sin(A + B) = sinCOSA + cosCSINA = cosA + cosB Vậy ta có: cosA + cosB + cosC < sinC + sinB Do đó, ta có HA + HB + HC < AB + AC. b) Ta có: AB + BC + CA = 2R(sinA + sinB + sinC) = 2R(sinA + sinB + sin(A + B)) = 2R(2sin(A + B/2)cos(A - B/2) + sin(A + B)) = 4Rsin(A + B/2)cos(A - B/2) + 2Rsin(A + B) Vậy ta cần chứng minh: 2RcosA + 2RcosB + 2RcosC < 2332 (4Rsin(A + B/2)cos(A - B/2) + 2Rsin(A + B)) Chia cả 2 vế cho 2R, ta có: cosA + cosB + cosC < 1166(2sin(A + B/2)cos(A - B/2) + sin(A + B)) Áp dụng bất đẳng thức tam giác, ta có: sin(A + B) > sinC = sin(A + B/2 + B/2) = sin(A + B/2)cos(B/2) + cos(A + B/2)sin(B/2) Vậy ta có: 2sin(A + B/2)cos(A - B/2) + sin(A + B) < 2sin(A + B/2)cos(A - B/2) + sin(A + B/2)cos(B/2) + cos(A + B/2)sin(B/2) = sin(A + B/2)(2cos(A - B/2) + cos(B/2)) + cos(A + B/2)sin(B/2) = sin(A + B/2)(2cos(A - B/2) + cos(B/2)) + sin(B/2)cos(A + B/2) = sin(A + B/2)(2cos(A - B/2) + cos(B/2) + cos(A + B/2)) Vậy ta có: cosA + cosB + cosC < 1166(2sin(A + B/2)cos(A - B/2) + sin(A + B)) < 1166(sin(A + B/2)(2cos(A - B/2) + cos(B/2) + cos(A + B/2))) Do đó, ta có HA + HB + HC < 2332(AB + BC + CA).

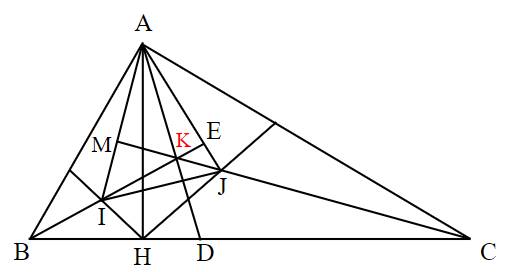
a) Ta có: ^ABH=^HAC (Cùng phụ với ^BAH) => 1/2^ABH=1/2^HAC => ^EBA=^EAC
^EAC+^BAE=^BAC=900. Mà ^EBA=^EAC => ^EBA+^BAE=900.
Xét tam giác ABE: ^EBA+^BAE=900 => ^AEB=900.
=> Tam giác ABE vuông tại E (đpcm)
b) Gọi M là giao điểm của CJ và AI.
Gọi K là giao điểm của BE và CM.
^ACH=^BAH (Cùng phụ với ^HAC) => 1/2^ACH=1/2^BAH => ^MAB=^ACM
^MAB+^MAC=900 => ^ACM+^MAC=900 => Tam giác AMC vuông tại M.
Xét tam giác AIJ: IE vuông góc AJ, JM vuông góc AI. Mà IE giao JM tại K.
=> K là trực tâm của tam giác AIJ => AK vuông góc IJ.
Xét tam giác ABC: BE là phân giác ^ABC, CM là phân giác ^ACB.
BE giac CM tại K => AK là phân giác ^BAC. Mà AD là phân giác ^BAC.
=> A,K,D thẳng hàng => AD vuông góc với IJ (đpcm)

Ta có: OA + OB + OC = OA + OB + OC = (OA + OB) + OC = AB + OC < AB + BC + CA (vì OC < BC) Vậy ta có: OA + OB + OC < AB + BC + CA (1) Ta cũng có: OA + OB + OC = OA + OB + OC = (OA + OC) + OB = AC + OB < AB + BC + CA (vì OB < AB) Vậy ta có: OA + OB + OC < AB + BC + CA (2) Từ (1) và (2), ta có: OA + OB + OC < AB + BC + CA Tương tự, ta có: OA + OB + OC = OA + OB + OC = (OB + OC) + OA = BC + OA > 0A + OB + OC (vì BC > 0A) Vậy ta có: OA + OB + OC > 0A + OB + OC (3) Ta cũng có: OA + OB + OC = OA + OB + OC = (OA + OB) + OC = AB + OC > 0A + OB + OC (vì AB > 0A) Vậy ta có: OA + OB + OC > 0A + OB + OC (4) Từ (3) và (4), ta có: OA + OB + OC > 0A + OB + OC Vậy ta có: 0A + OB + OC < AB + BC + CA < OA + OB + OC

Mom: Daisy. Dậy đi. Bữa sáng đã sẵn sàng rồi.
Daisy: OK, mẹ. Nhưng bây giờ là mấy giờ?
Mom: Bây giờ là 7 giờ.
Daisy: Cảm ơn mẹ.
Mom: Đây là bữa sáng, Daisy.
Daisy: Wow. Chúng ta ăn ngon quá.
Mom: Đúng vậy. Bữa sáng có trứng, mì và rau.
Daisy: Cảm ơn mẹ nhiều lắm.
Mom: Cảm ơn Daisy.
Mom: Daisy. Dậy đi. Bữa sáng đã sẵn sàng rồi.
Daisy: OK, mẹ. Nhưng bây giờ là mấy giờ?
Mom: Bây giờ là 7 giờ.
Daisy: Cảm ơn mẹ.
Mom: Đây là bữa sáng, Daisy.
Daisy: Wow. Chúng ta ăn ngon quá.
Mom: Đúng vậy. Bữa sáng có trứng, mì và rau.
Daisy: Cảm ơn mẹ nhiều lắm.
Mom: Cảm ơn Daisy.

e. ĐKXĐ: $x\geq \frac{1}{2}$
PT \(\Leftrightarrow \sqrt{(2x-1)-2\sqrt{2x-1}+1}+2\sqrt{(2x-1)-4\sqrt{2x-1}+4}+3\sqrt{(2x-1)-6\sqrt{2x-1}+9}=4\)
\(\Leftrightarrow \sqrt{(\sqrt{2x-1}-1)^2}+2\sqrt{(\sqrt{2x-1}-2)^2}+3\sqrt{(\sqrt{2x-1}-3)^2}=4\)
\(\Leftrightarrow |\sqrt{2x-1}-1|+2|\sqrt{2x-1}-2|+3|\sqrt{2x-1}-3|=4\)
Đặt $\sqrt{2x-1}-3=a$ thì:
$|a+2|+2|a+1|+3a=4$
Nếu $a\geq 0$ thì:
$a+2+2(a+1)+3a=4$
$\Leftrightarrow 6a+4=4\Leftrightarrow a=0\Leftrightarrow \sqrt{2x-1}=3\Leftrightarrow 2x-1=9\Leftrightarrow x=5$ (tm)
Nếu $-1\leq a<0$ thì:
$a+2+2(a+1)-3a=4$
$\Leftrightarrow 4=4$ (luôn đúng). Vậy là mọi giá trị $-1\leq a<0$ luôn thỏa mãn đề
$\Leftrightarrow -1\leq \sqrt{2x-1}-3<0$
$\Leftrightarrow 2\leq \sqrt{2x-1}<3\Leftrightarrow \frac{5}{2}\leq x< 5$
Nếu $-2\leq a< -1$ thì:
$a+2-2(a+1)-3a=4$
$\leftrightarrow -4a=4\Leftrightarrow a=-1$ (không tm)
Nếu $a< -2$ thì:
$-(a+2)-2(a+1)-3a=4$
$\Leftrightarrow -6a-4=4$
$\Leftrightarrow x=\frac{-8}{6}> -2$ (không tm)
Vậy $\frac{5}{2}\leq x\leq 5$
Lời giải:
ĐKXĐ: $x\geq \frac{1}{2}$
PT $\Leftrightarrow [(2x-1)-2\sqrt{2x-1}+1]+[(3x+1)-4\sqrt{3x+1}+4]=0$
$\Leftrightarrow (\sqrt{2x-1}-1)^2+(\sqrt{3x+1}-2)^2=0$
Vì $(\sqrt{2x-1}-1)^2\geq 0; (\sqrt{3x+1}-2)^2\geq 0$ với mọi $x\geq \frac{1}{2}$
Do đó để tổng của chúng bằng $0$ thì:
$\sqrt{2x-1}-1=\sqrt{3x+1}-2=0$
$\Leftrightarrow x=1$ (tm)

Thiên hà là một hệ thống lớn các thiên thể và vật chất liên kết với nhau bằng lực hấp dẫn, bao gồm sao, tàn dư sao, môi trường liên sao chứa khí, bụi vũ trụ và vật chất tối, một loại thành phần quan trọng nhưng chưa được hiểu rõ
Thiên hà là một hệ thống lớn các thiên thể được liên kết với nhau bằng lực hấp dẫn

Ta có số bé nhất có 2 chữ số là:10
=> Số liền trước của số bé nhất có 2 chữ số là:9
Vậy tổng của 2 số đó là :10+9=19
Số bé nhất có hai chữ số là: 10
⇒ Số liền trước của số bé nhất có hai chữ số là: 9
⇒ Tổng của số bé nhất có hai chữ số và số liền trước của nó là:
10+9=19
Đ/S: 19

\(\dfrac{3}{x}+\dfrac{x}{x+1}+\dfrac{x-3}{x}=\dfrac{13}{17}\left(x\ne0;x\ne-1\right)\)
\(\Rightarrow\dfrac{51\left(x+1\right)}{17x\left(x+1\right)}+\dfrac{17x^2}{17x\left(x+1\right)}+\dfrac{17\left(x-3\right)\left(x+1\right)}{17x\left(x+1\right)}=\dfrac{13x\left(x+1\right)}{17x\left(x+1\right)}\)
\(\)\(\Rightarrow51\left(x+1\right)+17x^2+17\left(x-3\right)\left(x+1\right)=13x\left(x+1\right)\)
\(\Rightarrow51x+51+17x^2+17\left(x^2-2x-3\right)=13x^2+13x\)
\(\Rightarrow34x^2-13x^2+17x-13x=0\)
\(\Rightarrow21x^2+4x=0\)
\(\Rightarrow x\left(21x+4\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\21x+4=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{4}{21}\end{matrix}\right.\)
(x-5)3=64=43
=>x-5=4
=>x=4+5=9
Vậy x=9