A = \(\frac12+\frac16+\frac{1}{12}+\cdots+\)

A = \(\frac{1}{1.1}\) + \(\frac{1}{2.3}\) + ... +

Số hạng thứ 80 của tổng A là: \(\frac{1}{80.81}\)

Tổng của 80 số hạng đầu tiên của dãy số trên là:

A = \(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+.\ldots+\frac{1}{80.81}\)

A = \(\frac11-\frac12+\frac12-\frac13+\cdots+\frac{1}{80}-\frac{1}{81}\)

A = \(\frac11\) - \(\frac{1}{81}\)

A = \(\frac{80}{81}\)

\(\dfrac{1}{2}=1.2\) (số hạng thứ nhất)

\(\dfrac{1}{6}=2.3\) (số hạng thứ hai)

\(\dfrac{1}{12}=\dfrac{1}{3.4}\) (số hạng thứ ba)

...

\(\dfrac{1}{80.81}\) (số hạng thứ 80)

Tổng 80 số hạng đó:

\(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{80.81}\)

\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{80}-\dfrac{1}{81}\)

\(=1-\dfrac{1}{81}\)

\(=\dfrac{80}{81}\)

( 2002 - 79 + 15 ) - ( -79 -15 )

= 2002 - 79 + 15 + 79 + 15

= 2002 -79 + 79 + 15 x 2

= 2002 + 30

= 2032

(2002 - 79 + 15) - (-79 - 15)

= 2002 - 79 + 15 + 79 + 15

= (15 + 15) + 2002 + (-79 + 79)

= 30 + 2002 + 0

= 2032

- 329 x (-15 - 101) - (25 - 440)

= 329 x 15 + 329 x 101 - 25 + 440

= 4935 + 33229 - 25 + 440

= (4935 - 25) + (33229 + 440)

= 4910 + 33669

= 38579

Olm chào em, em làm đúng rồi đó.

phép tính này có dư

Nhớ tick đó

Để tính số tiền mẹ thu được sau một năm, ta tính như sau: Số tiền gốc: 70.000.000 đồng Lãi suất năm: 7,2% = 0,072 Lãi một năm: 70.000.000 * 0,072 = 5.040.000 đồng Tổng số tiền sau một năm: 70.000.000 + 5.040.000 = 75.040.000 đồng Vậy, sau một năm, mẹ sẽ thu được 75.040.000 đồng, bao gồm cả lãi và gốc.

Giải:

Số tiền mà mẹ thu được sau khi gửi tiết kiệm một năm so với tiền gốc chiếm số phần trăm là:

100% + 7,2% = 107,2%

Sau một năm gửi tiết kiệm mẹ thu được số tiền cả gốc và lãi là:

70 000 000 x 107,2% = 75 040 000 (đồng)

Đáp số: 75 040 000 đồng

Tổng số phần bằng nhau là 7+1=8(phần)

Số lớn là \(72:8\times7=63\)

Số bé là 72-63=9

TH1: \(x< \dfrac{1}{2}\)

Phương trình sẽ trở thành:

\(1-2x+5-2x=6\)

=>6-4x=6

=>4x=0

=>x=0(nhận)

TH2: \(\dfrac{1}{2}< =x< \dfrac{5}{2}\)

Phương trình sẽ trở thành:

\(2x-1+5-2x=6\)

=>4=6(vô lý)

=>\(x\in\varnothing\)

TH3: \(x>=\dfrac{5}{2}\)

Phương trình sẽ trở thành:

2x-1+2x-5=6

=>4x=12

=>x=3(nhận)

|\(x\) + 7| = 2

\(\left[\begin{array}{l}x+7=-2\\ x+7=2\end{array}\right.\)

\(\left[\begin{array}{l}x=-2-7\\ x=2-7\end{array}\right.\)

\(\left[\begin{array}{l}x=-9\\ x=-5\end{array}\right.\)

Vậy \(x\in\left(-9;-5\right)\)

Nếu \(x=-9\) thay vào biểu thức C = \(-\frac57x^2-\frac34x+1\) ta có:

C = - \(\frac57\left(-9\right)^2\) - \(\frac43\left(-9\right)\) + 1

C = - \(\frac57.81+12\) + 1

C = \(-\frac{405}{7}\) + \(\frac{84}{7}+\frac77\)

C = - \(\frac{321}{7}+\frac77\)

C = \(\) - \(\frac{314}{7}\)

Nếu \(x=-5\) thay vào biểu thức C = \(-\frac57x^2-\frac{4}{3x}+1\) ta có:

C = - \(\frac57.\left(-5\right)^2-\frac43.\left(-5\right)+1\)

C = - \(\frac57.25+\frac{20}{3}+1\)

C = \(-\frac{125}{7}+\frac{20}{3}+1\)

C = \(-\frac{375}{21}+\frac{140}{21}+\frac{21}{21}\)

C = - \(\frac{235}{21}+\frac{21}{21}\)

C = - \(\frac{214}{21}\)

Bốn năm trước mẹ vẫn hơn con 30 tuổi

Hiệu số phần bằng nhau:

7 - 1 = 6 (phần)

Số tuổi của mẹ hiện nay:

30 : 6 × 7 + 4 = 39 (tuổi)

Số tuổi của con hiện nay:

39 - 30 = 9 (tuổi)

Bổ sung sơ đồ:

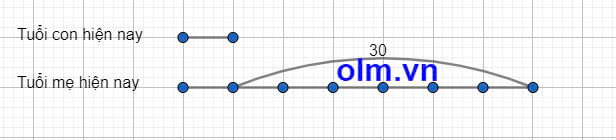
Theo bài ra ta có sơ đồ:

Theo sơ đồ ta có: