
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đời đường là đời thịnh trị nhất trong lịch sử trung hoa do hoàng đế Lý Thế Dân ngự trị đất nước. Chính ông đã cử Đường Huyền Trang đi lấy kinh, sau đó Ngô Thừa Ân đã hư cấu thêm thành Tây Du Kí


Lời giải:
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{bz-cy}{a}=\frac{cx-az}{b}=\frac{ay-bx}{c}$
$=\frac{abz-acy}{a^2}=\frac{bcx-abz}{b^2}=\frac{acy-bcx}{c^2}$
$=\frac{abz-acy+bcx-abz+acy-bcx}{a^2+b^2+c^2}=\frac{0}{a^2+b^2+c^2}=0$
$\Rightarrow bz-cy=cx-az=ay-bx=0$
$\Rightarrow bz=cy; cx=az; ay=bx$
$\Rightarrow \frac{y}{b}=\frac{z}{c}; \frac{z}{c}=\frac{x}{a}$
$\Rightarrow \frac{x}{a}=\frac{y}{b}=\frac{z}{c}$

vì \(x\) và y là hai đại lượng tỉ lệ thuận nên \(x\) = ky
Thay \(x\) = 3; y = -9 vào biểu thức: \(x\) = ky ta có:
3 = k.(-9) ⇒ k = 3 : (-9) = - \(\dfrac{1}{3}\)
⇒ \(x\) = - \(\dfrac{1}{3}\)y
với \(x\) = -1,5 ta có: -1,5 = - \(\dfrac{1}{3}\)y ⇒ y = -1,5.(-3) = 4,5

Lời giải:
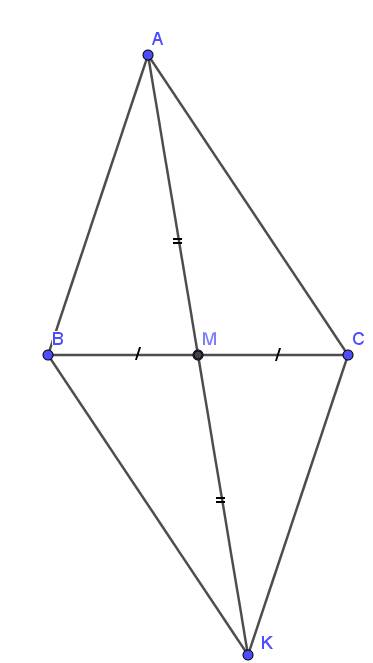
a. Xét tam giác $AMC$ và $KMB$ có:
$MC=MB$ (do $M$ là trung điểm $BC$)
$AM=KM$ (gt)
$\widehat{AMC}=\widehat{KMB}$ (đối đỉnh)
$\Rightarrow \triangle AMC=\triangle KMB$ (c.g.c)
và $\widehat{ACM}=\widehat{KBM}$
Mà 2 góc này ở vị trí so le trong nên $AC\parallel BK$
b.
Xét tam giác $ABM$ và $KCM$ có:
$BM=CM$
$AM=KM$
$\widehat{AMB}=\widehat{KMC}$ (đối đỉnh)
$\Rightarrow \triangle ABM=\triangle KCM$ (c.g.c)
$\Rightarrow \widehat{ABM}=\widehat{KCM}$
Mà 2 góc này ở vị trí so le trong nên $AB\parallel CK$


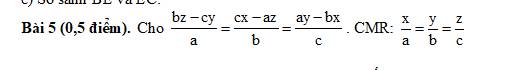
A