Gọi số ti vi mỗi loại mà cửa hàng bán được lần lượt là:

\(x;y;z\) (chiếc) \(x;y;z\) \(\in\)N^*

Thì số tiền thu được được việc bán mỗi loại ti vi lần lượt là:

20\(x;\) 18\(y\); 15\(z\) 

Theo bài ra ta có: 20\(x\) = 18\(y\) = 15\(z\);    \(x+y+z=62\)

⇒ \(y\) = \(\dfrac{20}{18}\)\(x\) = \(\dfrac{10}{9}\)\(x\)

    z = \(\dfrac{20}{15}\)\(x\) = \(\dfrac{4}{3}x\)

⇒ \(x+\dfrac{10}{9}x+\dfrac{4}{3}x=62\)

    \(x\left(1+\dfrac{10}{9}+\dfrac{4}{3}\right)=62\)

    \(\dfrac{31}{9}\)\(x\)                      = 62

        \(x\)                      = 62: \(\dfrac{31}{9}\)

        \(x\)                      =  18

         \(y\) = \(\dfrac{10}{9}.18=20\)

        \(z=\dfrac{4}{3}.18=24\)

Kết luận: Ti vi sam sung bán được 18 chiếc

                Ti vi LG bán được 20 chiếc

                Ti vi Xiaomi bán được 24 chiếc

`@` `\text {Ans}`

`\downarrow`

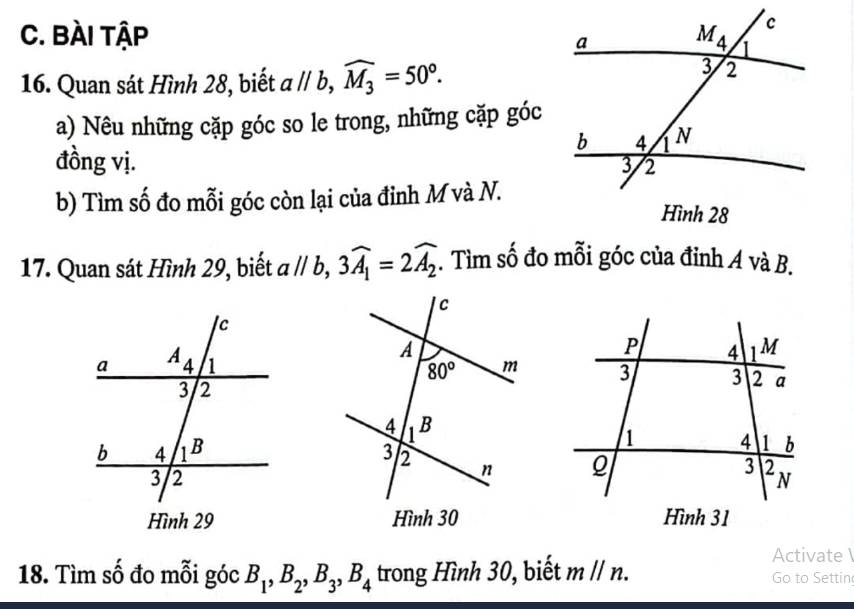
`16,`

`@` Các cặp góc đồng vị:

`+`\(\widehat {M_4}\) và \(\widehat {N_4}\)

`+`\(\widehat {M_1}\) và \(\widehat {N_1}\)

`+`\(\widehat {M_2}\) và \(\widehat {N_2}\)

`+`\(\widehat {M_3}\) và \(\widehat {N_3}\)

`@` Các cặp góc sole trong:

`+`\(\widehat {M_3} \) và \(\widehat {N_1}\)

`+`\(\widehat {M_2}\) và \(\widehat {N_4}\) 

`b,`

Ta có: \(\widehat {M_3} = \widehat {M_1} (\text {đối đỉnh})\)

`=>`\(\widehat {M_1}=50^0\)

\(\widehat {M_3}+\widehat {M_2}=180^0 (\text {kề bù})\)

`=>`\(50^0+\widehat {M_2}=180^0\)

`=>`\(\widehat {M_2}=180^0-50^0=130^0\)

\(\widehat {M_2}=\widehat {M_4} (\text {2 góc đối đỉnh})\)

`=>`\(\widehat {M_4} = 130^0\)

Vì \(\widehat {M_3}\) và \(\widehat {N_1}\) là `2` góc sole trong

`=>`\(\widehat {M_3}=\widehat {N_1}=50^0\)

\(\widehat {M_3}=\widehat {N_3}=50^0 (\text {2 góc đồng vị})\)

\(\widehat {M_2}=\widehat {N_2}=130^0 (\text {2 góc đồng vị})\)

\(\widehat {M_2}=\widehat {N_4}=130^0 (\text {2 góc slt})\)

`17,`

Vì \(\widehat {A_1}\) và \(\widehat {A_2}\) là `2` góc kề bù

`=>`\(\widehat {A_1}+\widehat {A_2}=180^0\)

\(3\widehat {A_1}=2\widehat {A_2}\) (gt)

`=>`\(\widehat{A_1}=\dfrac{2}{3}\cdot\widehat{A_2}\)

Thay \(\widehat{A_1}=\dfrac{2}{3}\widehat{A_2}\)

\(\dfrac{2}{3}\cdot\widehat{A_2}+\widehat{A_2}=180^0\)

`=>`\(\widehat{A_2}\left(\dfrac{2}{3}+1\right)=180^0\)

`=>`\(\widehat{A_2}\cdot\dfrac{5}{3}=180^0\)

`=>`\(\widehat{A_2}=180^0\div\dfrac{5}{3}\)

`=>`\(\widehat{A_2}=108^0\)

Vậy, số đo \(\widehat{A_2}=108^0\)

\(\widehat {A_1}+\widehat {A_2}=180^0 (\text {kề bù})\)

`=>`\(\widehat{A_1}+108^0=180^0\)

`=>`\(\widehat{A_1}=72^0\)

\(\widehat {A_1}=\widehat {A_3}=72^0 (\text {đối đỉnh})\)

\(\widehat {A_2}=\widehat {A_4}=108^0 (\text {đối đỉnh})\)

`@` Số đo các góc của đỉnh B:

`+`\(\widehat {A_4}=\widehat {B_4}=108^0 (\text {đồng vị})\)

`+`\(\widehat {A_2}=\widehat {B_2}=108^0 (\text {đồng vị})\)

`+`\(\widehat {A_3}=\widehat {B_1}=72^0 (\text {sole trong})\)

`+`\(\widehat {A_3}=\widehat {B_3}=72^0 (\text {đồng vị})\)

\(x+\dfrac{5}{2}=-\dfrac{1}{7}\)

\(\Rightarrow x=-\dfrac{1}{7}-\dfrac{5}{2}\)

\(\Rightarrow x=-\dfrac{2}{14}-\dfrac{35}{14}\)

\(\Rightarrow x=\dfrac{-2-35}{14}\)

\(\Rightarrow x=\dfrac{-37}{14}\)

a) Theo đề f(x) nhận -2 là nghiệm lấy -2 thay vào x ta có:

\(\left(-2\right)^2-2m+2=0\)

\(\Rightarrow4-2m+2=0\)

\(\Rightarrow6-2m=0\)

\(\Rightarrow2m=6\)

\(\Rightarrow m=3\)

b) Tìm được m ta có: \(f\left(x\right)=x^2+3x+2\)

\(\Rightarrow x^2+3x+2=0\)

\(\Rightarrow x^2+2x+x+2=0\)

\(\Rightarrow x\left(x+2\right)+\left(x+2\right)=0\)

\(\Rightarrow\left(x+2\right)\left(x+1\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x+2=0\\x+1=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-2\\x=-1\end{matrix}\right.\)

Vậy tập nghiệm của f(x) là: \(S=\left\{-2;-1\right\}\)

`@` `\text {Ans}`

`\downarrow`

`4,`

`a)`

\(f(x)=x(1-2x) + (2x^2 -x +4 )=0\)

`=> x-2x^2 + 2x^2-x+4=0`

`=> (x-x)+(-2x^2+2x^2)+4=0`

`=> 4=0 (\text {vô lí})`

Vậy, đa thức không có nghiệm.

`b)`

\(g(x) = x(x-5) - x(x+2)+ 7x=0\)

`=> x^2-5x-x^2-2x+7x=0`

`=> (x^2-x^2)+(-5x-2x+7x)=0`

`=> 0=0 (\text {luôn đúng})`

Vậy, đa thức có vô số nghiệm.

`c)`

\(h(x)= x(x-1) +1=0\)

`=> x^2-x+1=0`

Vì \(x^2 \ge 0\) \(\forall\) `x`

`=> x^2 - x + 1 \ge 1`\(\forall x\)

`1 \ne 0`

`=>` Đa thức vô nghiệm.

`\text {#KaizuulvG}`

Câu \(b,\) là \(x\in R\) cậu nhé!

`@` `\text {Ans}`

`\downarrow`

`a)`

Để `x=1` là nghiệm của đa thức, `x=1` phải t/m giá trị của đa thức `=0`

`m*1^2+3*1+5 =0`

`m+3+5=0`

`m+8=0`

`=> m=0-8`

`=> m=-8`

Vậy, để đa thức nhận `x=1` là nghiệm, thì `m` thỏa mãn giá trị là `m=-8`

`b)`

Thay `x=1` vào đa thức:

`6*1^2+m*1-1`

` =6+m-1`

` =6-1+m`

`= 5+m`

`5+m=0`

`=> m=0-5`

`=> m=-5`

Vậy, để đa thức trên nhận `x=1` là nghiệm, thì `m` thỏa mãn giá trị `m=-5`

`c)`

Thay `x=1` vào đa thức:

`1^5-3*1^2+m`

`= 1-3+m`

`= -2+m`

`-2+m=0`

`=> m=0-(-2)`

`=> m=0+2`

`=> m=2`

Vậy, để `x=1` là nghiệm của đa thức thì giá trị của `m` thỏa mãn `m=2.`

`\text {#KaizuulvG}`

Nửa chu vi hình chữ nhật là: 56 : 2 = 28 (m)

Chiều dài của khu vườn hình chữ nhật là:

84 : 4 = 21 (m)

Chiều rộng ban đầu của khu vườn hình chữ nhật là: 

28 - 21= 7 (m)

Kết luận: chiều dài ban đầu của hình chữ nhật là 21 m

               chiều rộng ban đầu của hình chữ nhật là 7 m

                    Giải

Nửa Chu vi khu vườn hình chữ nhật ban đầu là:

                                56:2= 28(m)

Chiều dài khu vườn hình chữ nhật ban đầu là: 

                                  84:4 = 21(m)

Chiều rộng khu vườn hình chữ nhật ban đầu là:

                                 28-21=7(m)

                                          Đ/S: Chiều dài: 21m

                                                    Chiều rộng: 7m

1.  

   1. a) Để tìm nghiệm của đa thức (x-2)(4-3x), ta giải phương trình (x-2)(4-3x) = 0. Khi đó, ta có hai trường hợp:

      • x - 2 = 0 hoặc 4 - 3x = 0
      • x = 2 hoặc x = 4/3

      Vậy nghiệm của đa thức (x-2)(4-3x) là x = 2 hoặc x = 4/3.

      b) Để tìm nghiệm của đa thức x^2 - 4, ta giải phương trình x^2 - 4 = 0. Khi đó, ta có:

      • (x-2)(x+2) = 0
      • x = 2 hoặc x = -2

      Vậy nghiệm của đa thức x^2 - 4 là x = 2 hoặc x = -2.

      c) Để tìm nghiệm của đa thức x^2 + √7, ta không thể giải phương trình x^2 + √7 = 0 vì không có số nào bình phương bằng √7. Vì vậy, đa thức này không có nghiệm trong tập số thực.

      d) Để tìm nghiệm của đa thức x^2 + 5x, ta giải phương trình x(x+5) = 0. Khi đó, ta có:

      • x = 0 hoặc x = -5

      Vậy nghiệm của đa thức x^2 + 5x là x = 0 hoặc x = -5.

      e) Để tìm nghiệm của đa thức x^2 + 5x - 6, ta giải phương trình (x+6)(x-1) = 0. Khi đó, ta có:

      • x + 6 = 0 hoặc x - 1 = 0
      • x = -6 hoặc x = 1

      Vậy nghiệm của đa thức x^2 + 5x - 6 là x = -6 hoặc x = 1.

      f) Để tìm nghiệm của đa thức x^2 + x + 1, ta không thể giải phương trình x^2 + x + 1 = 0 bằng phương pháp giải bình phương trình bởi vì hệ số của x^2 là 1 và không thể phân tích thành tích của hai số nguyên tố khác nhau. Vì vậy, đa thức này không có nghiệm trong tập số thực.

      h) Để tìm nghiệm của đa thức 7x^2 + 11x + 4, ta giải phương trình 7x^2 + 11x + 4 = 0 bằng cách sử dụng công thức giải phương trình bậc hai. Khi đó, ta có:

      • Δ = b^2 - 4ac = 11^2 - 474 = 121 - 112 = 9
      • x1 = (-b + √Δ) / 2a = (-11 + 3) / 14 = -4/7
      • x2 = (-b - √Δ) / 2a = (-11 - 3) / 14 = -7/2

      Vậy nghiệm của đa thức 7x^2 + 11x + 4 là x = -4/7 hoặc x = -7/2.

       

      (tham khảo

      20:22
   2.  

    

1. a) Để tìm nghiệm của đa thức (x-2)(4-3x), ta giải phương trình (x-2)(4-3x) = 0. Khi đó, ta có hai trường hợp:

   • x - 2 = 0 hoặc 4 - 3x = 0
   • x = 2 hoặc x = 4/3

   Vậy nghiệm của đa thức (x-2)(4-3x) là x = 2 hoặc x = 4/3.

   b) Để tìm nghiệm của đa thức x^2 - 4, ta giải phương trình x^2 - 4 = 0. Khi đó, ta có:

   • (x-2)(x+2) = 0
   • x = 2 hoặc x = -2

   Vậy nghiệm của đa thức x^2 - 4 là x = 2 hoặc x = -2.

   c) Để tìm nghiệm của đa thức x^2 + √7, ta không thể giải phương trình x^2 + √7 = 0 vì không có số nào bình phương bằng √7. Vì vậy, đa thức này không có nghiệm trong tập số thực.

   d) Để tìm nghiệm của đa thức x^2 + 5x, ta giải phương trình x(x+5) = 0. Khi đó, ta có:

   • x = 0 hoặc x = -5

   Vậy nghiệm của đa thức x^2 + 5x là x = 0 hoặc x = -5.

   e) Để tìm nghiệm của đa thức x^2 + 5x - 6, ta giải phương trình (x+6)(x-1) = 0. Khi đó, ta có:

   • x + 6 = 0 hoặc x - 1 = 0
   • x = -6 hoặc x = 1

   Vậy nghiệm của đa thức x^2 + 5x - 6 là x = -6 hoặc x = 1.

   f) Để tìm nghiệm của đa thức x^2 + x + 1, ta không thể giải phương trình x^2 + x + 1 = 0 bằng phương pháp giải bình phương trình bởi vì hệ số của x^2 là 1 và không thể phân tích thành tích của hai số nguyên tố khác nhau. Vì vậy, đa thức này không có nghiệm trong tập số thực.

   h) Để tìm nghiệm của đa thức 7x^2 + 11x + 4, ta giải phương trình 7x^2 + 11x + 4 = 0 bằng cách sử dụng công thức giải phương trình bậc hai. Khi đó, ta có:

   • Δ = b^2 - 4ac = 11^2 - 474 = 121 - 112 = 9
   • x1 = (-b + √Δ) / 2a = (-11 + 3) / 14 = -4/7
   • x2 = (-b - √Δ) / 2a = (-11 - 3) / 14 = -7/2

   Vậy nghiệm của đa thức 7x^2 + 11x + 4 là x = -4/7 hoặc x = -7/2.

    

   tham khảo

   20:22
2.  

Gọi số lạng bạc  của mỗi phần là: \(x\) (\(x\) > 0) (lạng)

Số bạc của 8 người hạng giáp là: \(x\) \(\times\) 7 \(\times\) 8 = 56\(x\) (lạng)

Số bạc của 20 người hạng Ất là: \(x\times\)5\(\times\)20 = 100\(x\) (lạng)

Số bạc của 300 người hạng Bính là: \(x\times\)2\(\times\)300 = 600\(x\) (lạng)

Theo bài ra ta có: 56\(x\) + 100\(x\)+ 600\(x\) = 5292

                                       756\(x\) = 5292

                                             \(x\) = 7

Vậy mỗi phần có số lạng bạc là : 7 lạng

Số lạng bạc mà mỗi người hạng Giáp nhận được là:

7 \(\times\) 7 = 49 (lạng)

Số lạng bạc mà mỗi người hạng Ất nhận được là:

7 \(\times\) 5 = 35 (lạng)

Số lạng bạc mà mỗi người hạng Bính nhận được là: 

7 \(\times\) 2 = 14 (lạng)

Kết luận: Mỗi người hạng Giáp nhận được 49 lạng bạc

              Mỗi người hạng Ất nhận được 35 lạng bạc

             Mỗi người hạng Bính nhận được 14 lạng bạc

`(x-2):(x-1)=(x+4)(x+7)`

\(< =>\dfrac{x-2}{x-1}=\dfrac{x+4}{x+7}\left(x\ne1;x\ne-7\right)\)

`=>(x-2)(x+7)=(x+4)(x-1)`

`<=>x^2 +7x-2x-14=x^2 -x+4x-4`

`<=>x^2 +5x-14-x^2 -3x+4=0`

`<=>2x-10=0`

`<=>2x=10`

`<=>x=5(tm)`