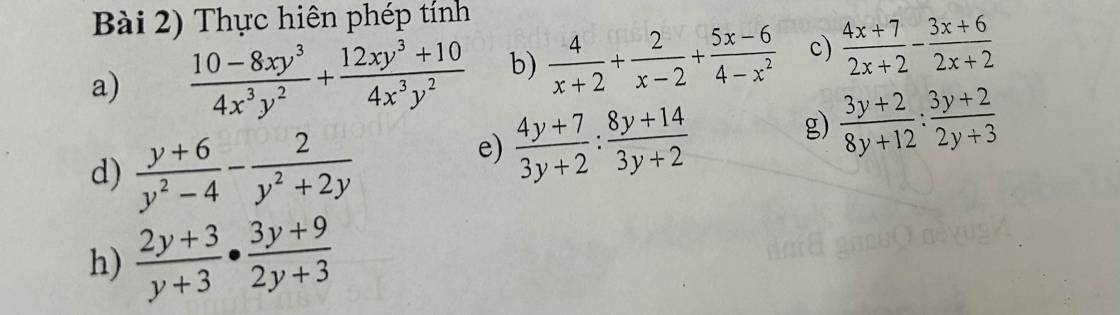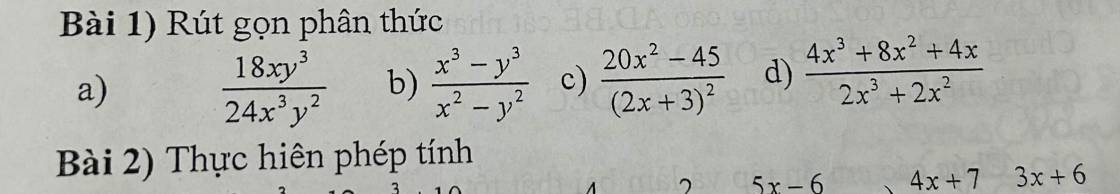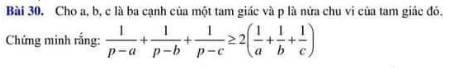Giúp mình câu 10 và câu 11 với xong mình tích cho
Giúp mình câu 10 và câu 11 với xong mình tích cho
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.






a.
$=\frac{10-8xy^3+12xy^3+10}{4x^3y^2}=\frac{20+4xy^3}{4x^3y^2}$
$=\frac{5+xy^3}{x^3y^2}$
b.
$=\frac{4(x-2)+2(x+2)}{(x+2)(x-2)}+\frac{6-5x}{(x-2)(x+2)}$
$=\frac{6x-4}{(x+2)(x-2)}+\frac{6-5x}{(x-2)(x+2)}$
$=\frac{x+2}{(x-2)(x+2)}=\frac{1}{x-2}$
c.
$=\frac{4x+7-(3x+6)}{2x+2}=\frac{x+1}{2(x+1)}=\frac{1}{2}$
d.
$=\frac{y+6}{(y-2)(y+2)}-\frac{2}{y(y+2)}$
$=\frac{y(y+6)-2(y-2)}{y(y+2)(y-2)}=\frac{y^2+4y+4}{y(y+2)(y-2)}=\frac{(y+2)^2}{y(y+2)(y-2)}=\frac{y+2}{y(y-2)}$
e.
$=\frac{4y+7}{3y+2}.\frac{3y+2}{8y+14}=\frac{4y+7}{8y+14}=\frac{4y+7}{2(4y+7)}=\frac{1}{2}$
g.
$=\frac{3y+2}{4(2y+3)}.\frac{2y+3}{3y+2}=\frac{1}{4}$
h.
$=\frac{2y+3}{y+3}.\frac{3(y+3)}{2y+3}=3$

Lời giải:
a. $=\frac{6xy^2.3y}{6xy^2.4x^2}=\frac{3y}{4x^2}$
b.
$=\frac{(x-y)(x^2+xy+y^2)}{(x-y)(x+y)}=\frac{x^2+xy+y^2}{x+y}$
c.
$=\frac{5(4x^2-9)}{(2x+3)^2}=\frac{5(2x-3)(2x+3)}{(2x+3)^2}=\frac{5(2x-3)}{2x+3}$
d.
$=\frac{4x(x^2+2x+1)}{2x^2(x+1)}=\frac{4x(x+1)^2}{2x^2(x+1)}=\frac{2(x+1)}{x}$

Lời giải:
a. Bạn tự vẽ hình
b. PT hoành độ giao điểm của $(d), (d')$:
$x+2=-2x+8\Leftrightaarrow 3x=6\Leftrightarrow x=2$
$y=x+2=2+2=4$
Vậy $A$ có tọa độ $(2,4)$
$B\in Ox$ nên $y_B=0$
$B\in (d)$ nên $y_B=x_B+2\Rightarrow x_B=y_B-2=0-2=-2$
Vậy $B(-2,0)$
$C\in Ox$ nên $y_C=0$
$C\in (d')$ nên $y_C=-2x_C+8\Rightarrow x_C=\frac{y_C-8}{-2}=\frac{-8}{-2}=4$
Vậy $C(4,0)$
Diện tích tam giác $ABC$:
$S_{ABC}=\frac{d(A,BC).BC}{2}=\frac{d(A,Ox).BC}{2}=\frac{|y_A|(|x_B|+|x_C|)}{2}=\frac{4(2+4)}{2}=12$ (đvdt)

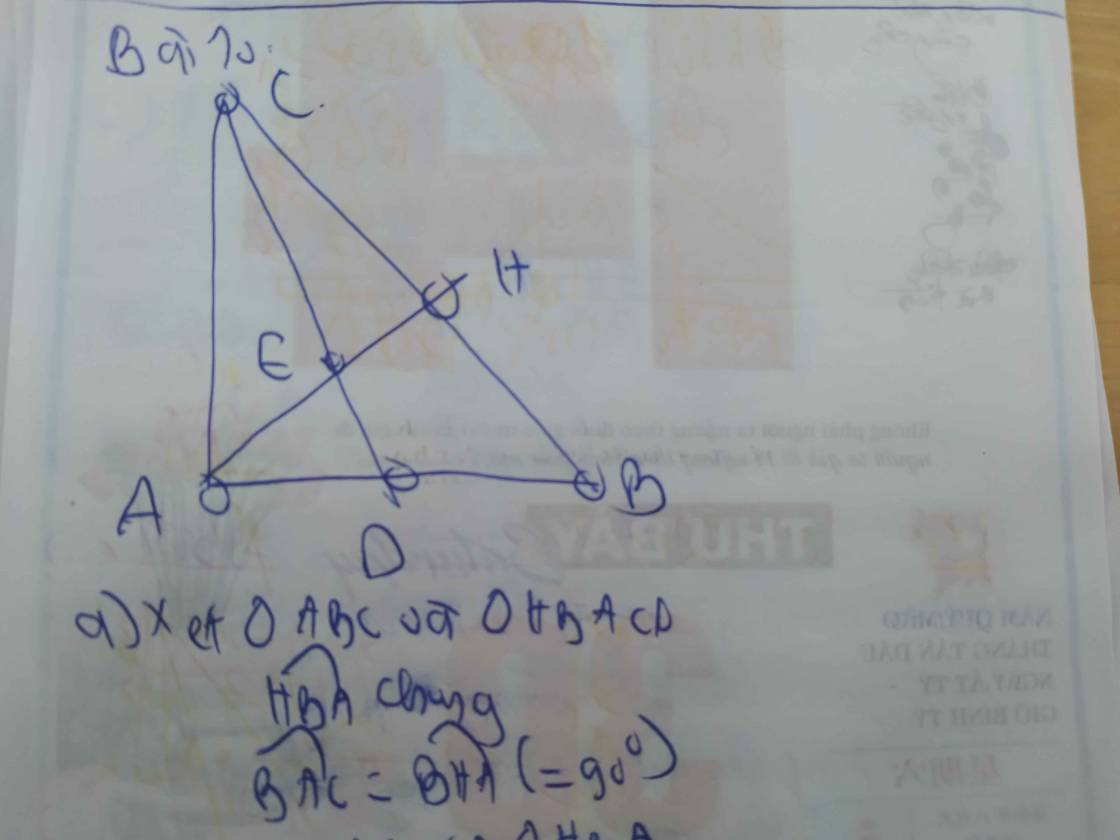
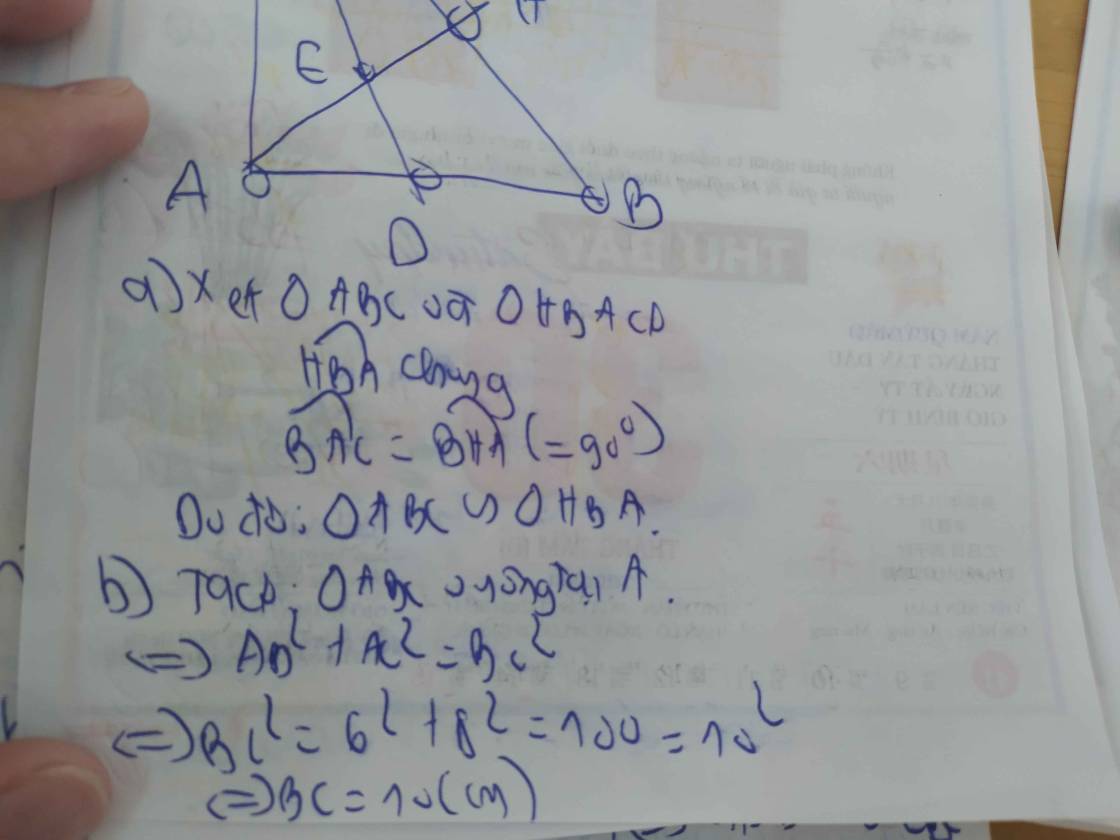
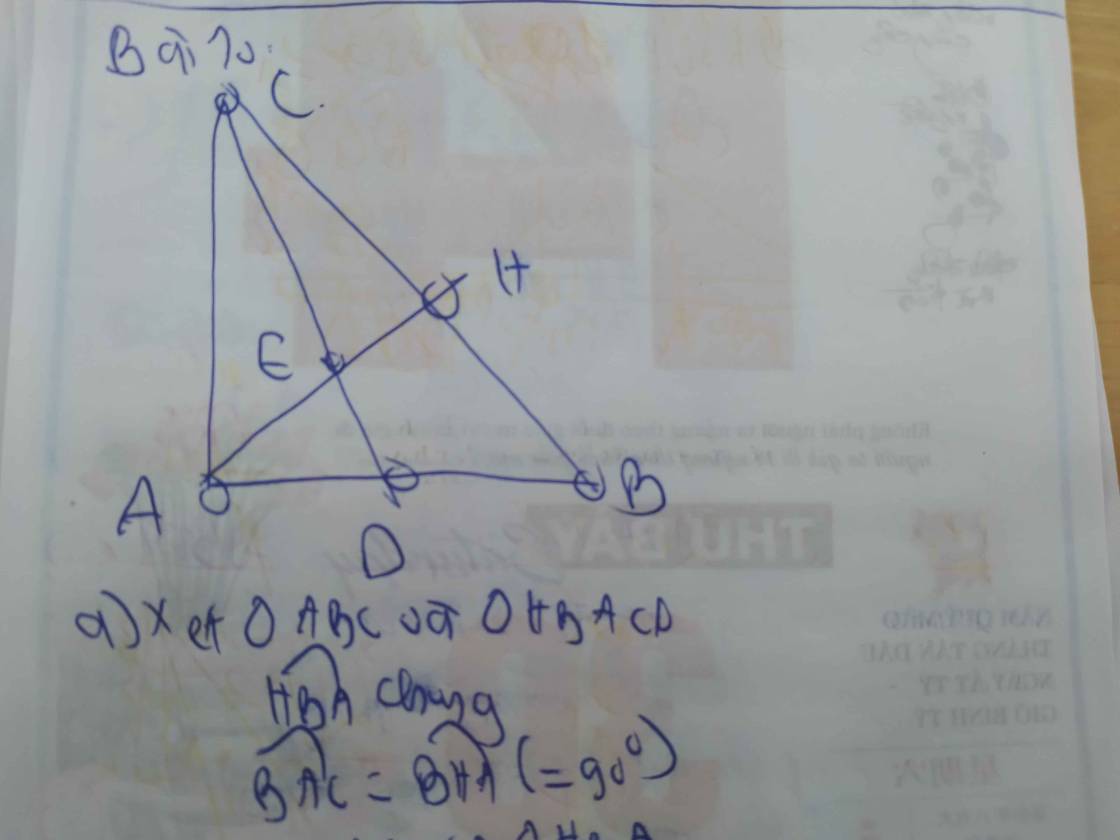
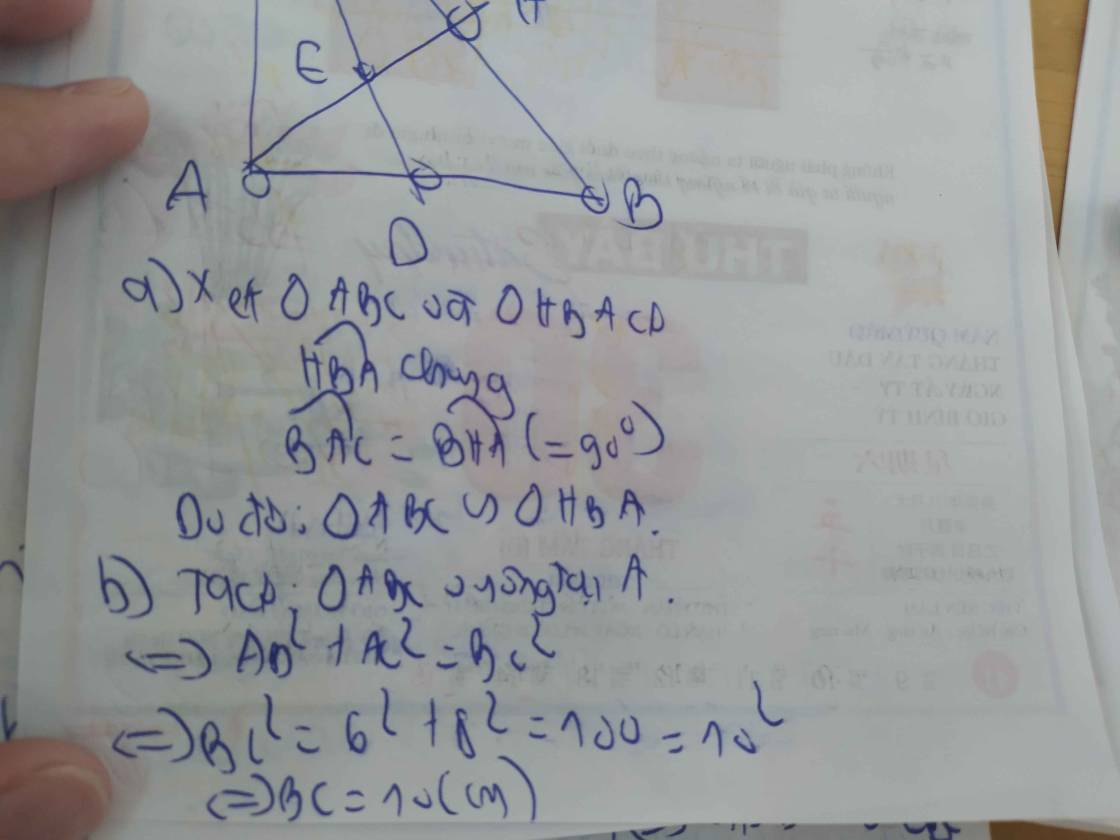
1: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
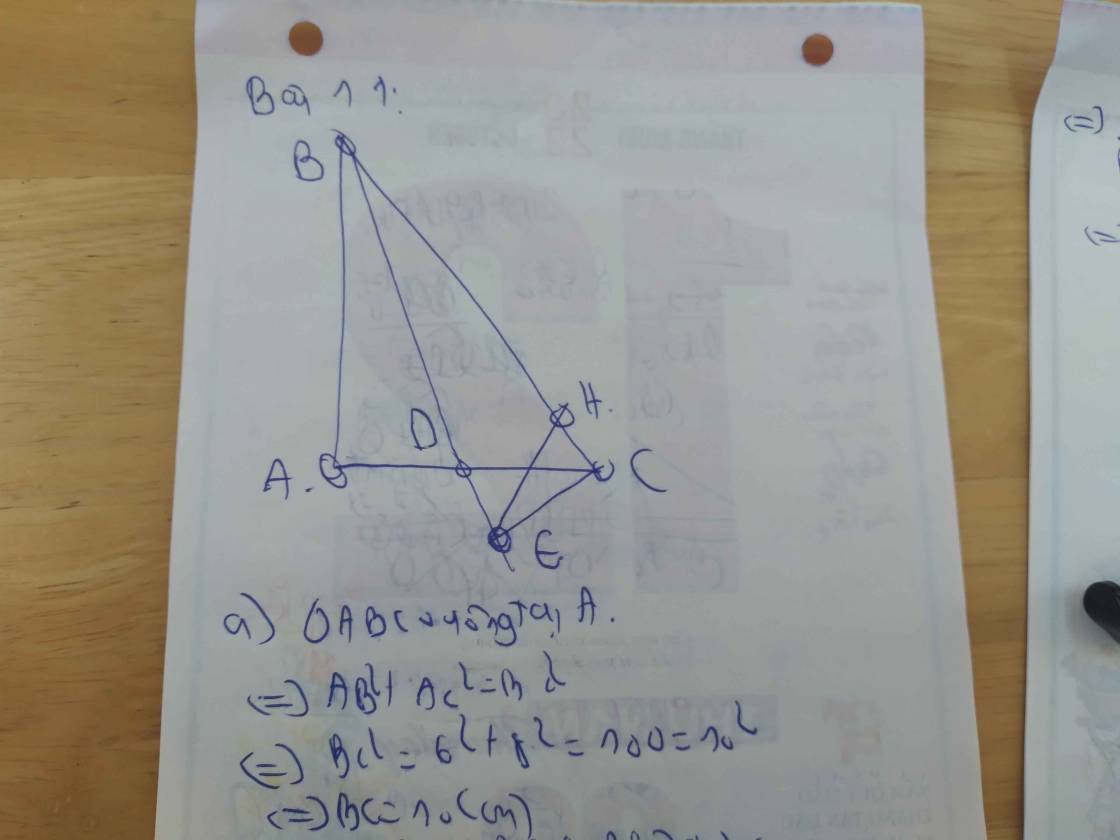
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100=10^2\)
=>BC=10(cm)
ΔABC~ΔHBA
=>\(\dfrac{AB}{HB}=\dfrac{BC}{BA}=\dfrac{AC}{HA}\)
=>\(\dfrac{6}{HB}=\dfrac{10}{6}=\dfrac{8}{HA}\)
=>\(HA=6\cdot\dfrac{8}{10}=4,8\left(cm\right);HB=6\cdot\dfrac{6}{10}=3,6\left(cm\right)\)
2: Xét ΔMAB vuông tại A và ΔMIC vuông tại I có
\(\widehat{AMB}=\widehat{IMC}\)(hai góc đối đỉnh)
Do đó: ΔMAB~ΔMIC
=>\(\dfrac{MA}{MI}=\dfrac{MB}{MC}\)
=>\(MA\cdot MC=MB\cdot MI\)

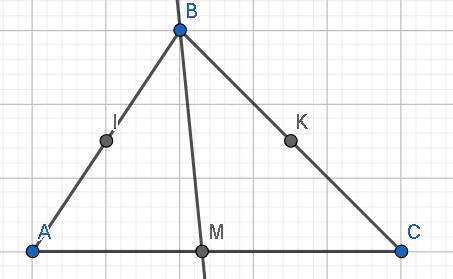
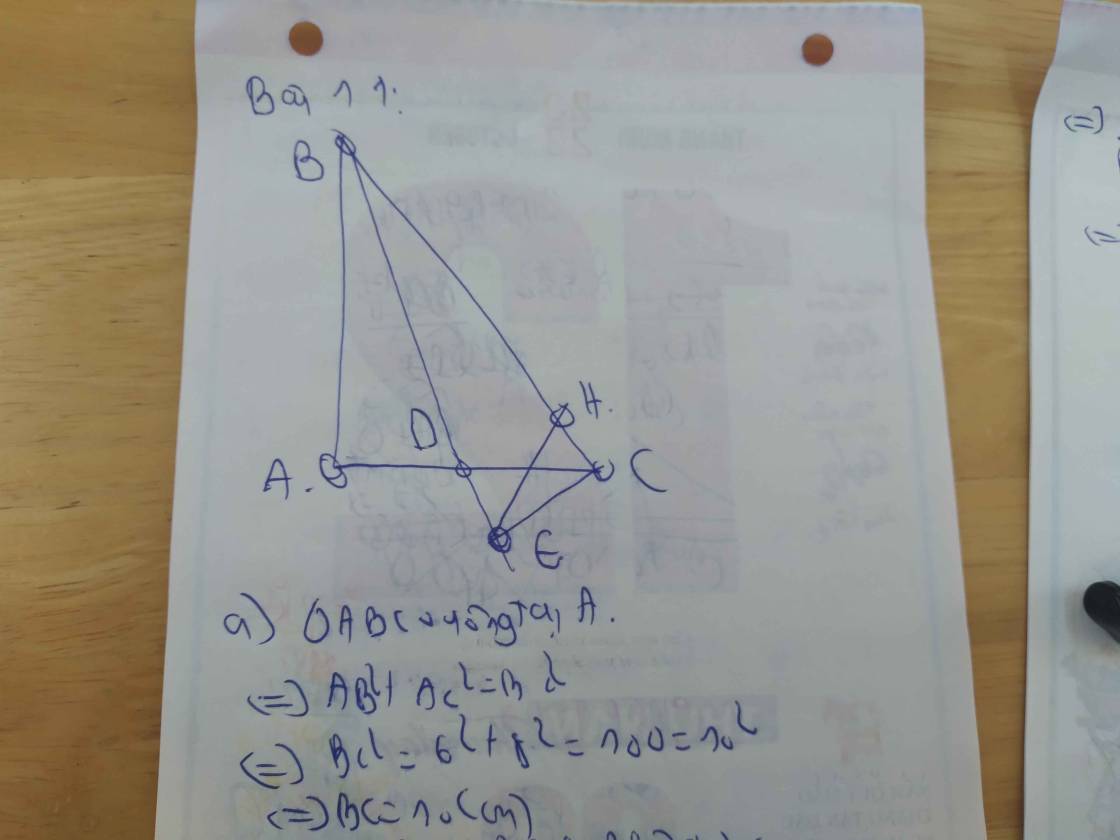
a: Xét ΔBAC có I,K lần lượt là trung điểm của BA,BC
=>IK là đường trung bình của ΔBAC
=>\(IK=\dfrac{AC}{2}=\dfrac{7}{2}=3,5\left(cm\right)\)
b: Xét ΔBAC có BM là phân giác
nên \(\dfrac{MA}{MC}=\dfrac{BA}{BC}\)
=>\(\dfrac{MA}{MC}=\dfrac{2AI}{2BK}=\dfrac{AI}{BK}\)
=>\(MA\cdot BK=MC\cdot AI\)

Lời giải:
Áp dụng BĐT Cauchy-Schwarz:
$\frac{1}{p-a}+\frac{1}{p-b}\geq \frac{4}{p-a+p-b}=\frac{4}{2p-a-b}=\frac{4}{c}$
$\frac{1}{p-b}+\frac{1}{p-c}\geq \frac{4}{p-b+p-c}=\frac{4}{a}$
$\frac{1}{p-a}+\frac{1}{p-c}\geq \frac{4}{p-a+p-c}=\frac{4}{b}$
Cộng theo vế 3 BĐT trên và thu gọn thì:
$\frac{1}{p-a}+\frac{1}{p-b}+\frac{1}{p-c}\geq 2(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})$
Ta có đpcm
Dấu "=" xảy ra khi $a=b=c$