D E F H M B C A K G

Nối E với F và nối K với F

Ta có

E và F cùng nhìn BC dưới 1 góc \(90^o\) => BCEF là tứ giác nội tiếp

\(\Rightarrow\widehat{BEK}=\widehat{KCF}\) (góc nt cùng chắn cung BF) và

\(\widehat{CFE}=\widehat{CBE}\) (góc nt cùng chắn cung CE) (1)

Xét tg BKE và tg FKC có

\(\widehat{BEK}=\widehat{KCF}\) (cmt)

\(\widehat{EKC}\) chung

\(\Rightarrow\widehat{KBE}=\widehat{KFC}\) (2)

Từ (1) và (2) \(\Rightarrow\widehat{KBE}+\widehat{CBE}=\widehat{KFC}+\widehat{CFE}\)

Mà \(\widehat{KBE}+\widehat{CBE}=\widehat{KBC}=180^o\)

\(\Rightarrow\widehat{KFC}+\widehat{CFE}=180^o\)

 => E; F; K thẳng hàng

A B C D E I H K F O G

a/

Xét \(\Delta ABC\)

AD và BE cắt nhau tại H (gt) 

\(\Rightarrow CH\perp AB\) (trong tam giác 3 đường cao đồng quy)

b/ Gọ F là giao của CH với AB ta có

F và D cùng nhìn BH dưới 1 góc \(90^o\) => F và H nằm trên đường tròn đường kính BH => Tứ giác BFHD là tứ giác nội tiếp)

Ta có

\(sđ\widehat{ABC}=\dfrac{1}{2}sđcungFHD\) (góc nt đường tròn)

\(sđ\widehat{FHD}=\dfrac{1}{2}sđcungFBD\) (góc nt đường tròn)

\(\Rightarrow sđ\widehat{ABC}+sđ\widehat{FHD}=\dfrac{1}{2}\left(sđcungFHD+sđcungFBD\right)\)

Mà \(sđcungFHD+sđcungFBD=360^o\)

\(\Rightarrow sđ\widehat{ABC}+sđ\widehat{FHD}=\dfrac{1}{2}.360^o=180^o\)

Mà \(\widehat{CHI}+\widehat{FHD}=\widehat{FHC}=180^o\)

\(\Rightarrow\widehat{CHI}=\widehat{ABC}\) (cùng bù với \(\widehat{FHD}\) ) (1)

Xét (O) có 

\(\widehat{ABC}=\widehat{AIC}\) (góc nt đường tròn cùng chắn cung AC) (2)

Từ (1) và (2) \(\Rightarrow\widehat{CHI}=\widehat{AIC}\) => tg CHI cân tại C

c/

Chứng minh tương tự ta cũng có CHK là tg cân tại C

Ta có

\(BE\perp AC\left(gt\right)\Rightarrow AC\perp HK\)

\(\Rightarrow EH=EK\) (trong tg cân đường cao xp từ đỉnh tg cân đồng thời là đường trung tuyến)

=> H đối xứng K qua AC

d/ Gọi G là giao của CO với (O)

Ta có tg CHK cân tại C (cmt)

=> CK=CH

Mà tg CHI cân tại C (cmt) => CH=CI

=> CK=CI => tg CKI cân tại C (3)

Ta có

\(sđ\widehat{CKI}=\dfrac{1}{2}sđcungCI\) (góc nt (O))

\(sđ\widehat{CIK}=\dfrac{1}{2}sđcungCK\) (góc nt (O))

\(\Rightarrow sđcungCI=sđcungCK\)

Ta có 

sđ cung CIG = sđ cung CKG \(=180^o\)

=> sđ cung CIG - sđ cung CI = sđ cung CKG - sđ cung CK

=> sđ cung GBI = sđ cung GAK

Ta có

\(sđ\widehat{ICG}=\dfrac{1}{2}sđcungGBI\) (góc nt (O))

\(sđ\widehat{KCG}=\dfrac{1}{2}sđcungGAK\) (góc nt (O))

\(\Rightarrow\widehat{ICG}=\widehat{KCG}\) => CG là phân giác của \(\widehat{KCI}\) (4)

Từ (3) và (4) => \(OC\perp KI\) (trong tg cân đường phân giác của góc ở đỉnh tg cân đồng thời là đường cao)

e/

Ta có E và D cùng nhìn CH dưới 1 góc \(90^o\) => CDHE là tứ giác nội tiếp

\(\Rightarrow\widehat{HDE}=\widehat{ECF}\) (góc nt cùng chắn cung HE) (5)

Ta có F và E cùng nhìn BC dưới 1 góc \(90^o\) => BCEF là tứ giác nt

\(\Rightarrow\widehat{ABK}=\widehat{ECF}\) (góc nt cùng chắn cung EF) (6)

Xét (O) có

\(\widehat{ABK}=\widehat{AIK}\) (góc nt cùng chắn cung AK) (7)

Từ (5) (6) (7) \(\Rightarrow\widehat{HDE}=\widehat{AIK}\) mà 2 góc này ở vị trí đồng vị nên

=> ED//KI 

Mà \(OC\perp KI\left(cmt\right)\)

\(\Rightarrow OC\perp ED\)

Bạn nhập lại đề nhé ! 

Xem lại đề.

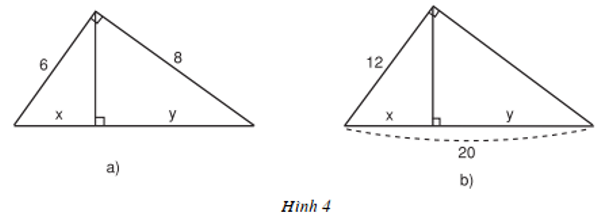
Hình a/

Áp dụng định lý Pitago:

$x+y=\sqrt{6^2+8^2}=10$ 

Áp dụng hệ thức lượng trong tam giác vuông:

$6^2=x(x+y)=10x\Rightarrow x=3,6$ 

$8^2=y(y+x)=10y\Rightarrow y=6,4$ 

Hình b/

Áp dụng hệ thức lượng trong tam giác vuông:

$12^2=x(x+y)=20x$

$\Rightarrow x=\frac{12^2}{20}=7,2$ 

$y=20-x=20-7,2=12,8$ 

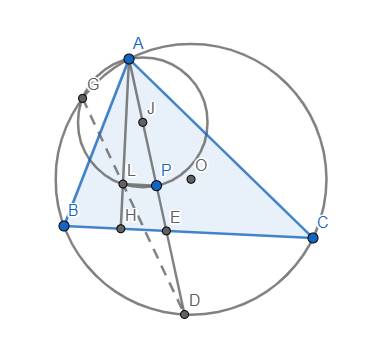
a) Gọi J là tâm đường tròn (AP)

 Xét đường tròn (J) có đường kính AP, \(L\in\left(J\right)\) nên \(\widehat{ALP}=90^o\) hay \(AH\perp LP\) tại L.

 Lại có \(AH\perp BC\) nên LP // BC.

 \(\Rightarrow\widehat{DPL}=\widehat{DEB}\) 

 Mặt khác, \(\widehat{DEB}=\dfrac{sđ\stackrel\frown{AC}+sđ\stackrel\frown{BD}}{2}\) \(=\dfrac{sđ\stackrel\frown{AC}+sđ\stackrel\frown{CD}}{2}\) \(=\dfrac{sđ\widehat{AD}}{2}\) \(=\widehat{AGD}\)

 Tứ giác AGLP nội tiếp nên \(\widehat{DPL}=\widehat{AGL}\)

 Từ đó suy ra \(\widehat{AGD}=\widehat{AGL}\)

 Hơn nữa, L, D nằm cùng phia đối với đường thẳng GA nên suy ra G, L, D thẳng hàng (đpcm).

Lời giải:
Giả sử cần a người và b ngày để hoàn thành xong công việc.

Theo bài ra ta có:

$ab=(a-1)(b+2)=(a+4)(b-4)$

$\Leftrightarrow ab=ab+2a-b-2=ab-4a+4b-16$

$\Leftrightarrow 2a-b=2$ và $-4a+4b=16$

Giải hpt trên ta có: $a=6; b=10$

Vậy cần 6 thợ và 10 ngày để sửa được ngôi nhà.

Cần 6thợ và 10ngày để xog công việc

\(A=\dfrac{2\left(3+\sqrt{5}\right)}{4+\sqrt{6+2\sqrt{5}}}+\dfrac{2\left(3-\sqrt{5}\right)}{4-\sqrt{6-2\sqrt{5}}}=\dfrac{2\left(3+\sqrt{5}\right)}{4+\sqrt{\left(\sqrt{5}+1\right)^2}}+\dfrac{2\left(3-\sqrt{5}\right)}{4-\sqrt{\left(\sqrt{5}-1\right)^2}}\)

\(=\dfrac{2\left(3+\sqrt{5}\right)}{5+\sqrt{5}}+\dfrac{2\left(3-\sqrt{5}\right)}{5-\sqrt{5}}=\dfrac{2\left(3+\sqrt{5}\right)\left(5-\sqrt{5}\right)+2\left(3-\sqrt{5}\right)\left(5+\sqrt{5}\right)}{\left(5-\sqrt{5}\right)\left(5+\sqrt{5}\right)}\)

\(=\dfrac{40}{20}=2\)

a. Câu này đơn giản em tự giải

b.

Xét hai tam giác OIM và OHN có:

\(\left\{{}\begin{matrix}\widehat{OIM}=\widehat{OHN}=90^0\\\widehat{MON}\text{ chung}\\\end{matrix}\right.\) \(\Rightarrow\Delta OIM\sim\Delta OHN\left(g.g\right)\)

\(\Rightarrow\dfrac{OI}{OH}=\dfrac{OM}{ON}\Rightarrow OI.ON=OH.OM\)

Cũng từ 2 tam giác đồng dạng ta suy ra \(\widehat{OMI}=\widehat{ONH}\)

Tứ giác OAMI nội tiếp (I và A cùng nhìn OM dưới 1 góc vuông)

\(\Rightarrow\widehat{OAI}=\widehat{OMI}\)

\(\Rightarrow\widehat{OAI}=\widehat{ONH}\) hay \(\widehat{OAI}=\widehat{ONA}\)

c.

Xét hai tam giác OAI và ONA có:

\(\left\{{}\begin{matrix}\widehat{OAI}=\widehat{ONA}\left(cmt\right)\\\widehat{AON}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OAI\sim\Delta ONA\left(g.g\right)\)

\(\Rightarrow\dfrac{OA}{ON}=\dfrac{OI}{OA}\Rightarrow OI.ON=OA^2=OC^2\) (do \(OA=OC=R\))

\(\Rightarrow\dfrac{OC}{ON}=\dfrac{OI}{OC}\)

Xét hai tam giác OCN và OIC có:

\(\left\{{}\begin{matrix}\dfrac{OC}{ON}=\dfrac{OI}{OC}\\\widehat{CON}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OCN\sim\Delta OIC\left(g.g\right)\)

\(\Rightarrow\widehat{OCN}=\widehat{OIC}=90^0\) hay tam giác ACN vuông tại C

\(\widehat{ABC}\) là góc nt chắn nửa đường tròn \(\Rightarrow BC\perp AB\)

Áp dụng hệ thức lượng trong tam giác vuông ACN với đường cao BC:

\(BC^2=BN.BA=BN.2BH=2BN.BH\) (1)

O là trung điểm AC, H là trung điểm AB \(\Rightarrow OH\) là đường trung bình tam giác ABC

\(\Rightarrow OH=\dfrac{1}{2}BC\)

Xét hai tam giác OHN và EBC có:

\(\left\{{}\begin{matrix}\widehat{OHN}=\widehat{EBC}=90^0\\\widehat{ONH}=\widehat{ECB}\left(\text{cùng phụ }\widehat{IEB}\right)\end{matrix}\right.\)  \(\Rightarrow\Delta OHN\sim\Delta EBC\left(g.g\right)\)

\(\Rightarrow\dfrac{OH}{EB}=\dfrac{HN}{BC}\Rightarrow HN.EB=OH.BC=\dfrac{1}{2}BC^2\)

\(\Rightarrow BC^2=2HN.EB\) (2)

(1);(2) \(\Rightarrow BN.BH=HN.BE\)

\(\Rightarrow BN.BH=\left(BN+BH\right).BE\)

\(\Rightarrow\dfrac{1}{BE}=\dfrac{BN+BH}{BN.BH}=\dfrac{1}{BH}+\dfrac{1}{BN}\) (đpcm)

Đề bài là sao nhỉ? Em có nhầm lẫn chỗ nào không? Vì đề đã cho sẵn người 1 làm riêng trong 8 giờ xong và người 2 làm riêng trong 12 giờ xong nên đó chính là đáp số rồi.

Trình bày ngắn gọn hướng giải, chi tiết tỉ mỉ em tự thực hiện

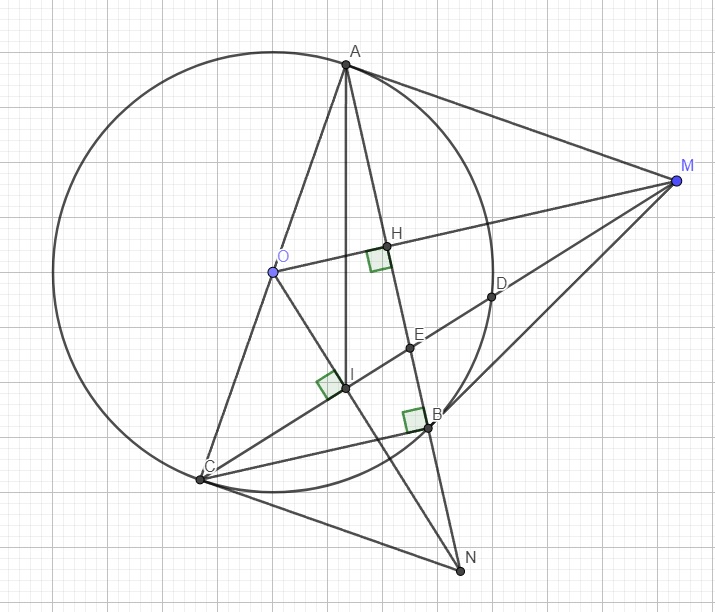
a.

AD vuông góc MO tại H \(\Rightarrow HA=HD\)

\(\Rightarrow\Delta_{\perp}OHA=\Delta_{\perp}OHD\left(c.g.c\right)\)

\(\Rightarrow\widehat{HOA}=\widehat{HOD}\)

\(\Rightarrow\Delta MOA=\Delta MOD\left(c.g.c\right)\)

\(\Rightarrow\widehat{MDO}=\widehat{MAO}=90^0\)

\(\Rightarrow MD\) là tiếp tuyến

b.

\(\widehat{MAB}=\widehat{MCA}\) (góc nt và góc tạo bởi tiếp tuyến - dây cung cùng chắn AB)

\(\Rightarrow\Delta MAB\sim\Delta MCA\)

\(\Rightarrow\dfrac{MA}{MC}=\dfrac{MB}{MA}\Rightarrow MA^2=MB.MC\)

Hệ thức lượng trong tam giác vuông MAO với đường cao AH:

\(MA^2=MH.MO\)

\(\Rightarrow MB.MC=MH.MO\Rightarrow\dfrac{MB}{MO}=\dfrac{MH}{MC}\)

Lại có \(\widehat{HMB}\) chung

\(\Rightarrow\Delta MHB\sim\Delta MCO\left(c.g.c\right)\)

c.

MA, MD là tiếp tuyến nên các tam giác MAO, MDO vuông

\(\Rightarrow M,A,D,O\) thuộc đường tròn đường kính MO

I là trung điểm BC \(\Rightarrow OI\perp BC\)

\(\Rightarrow\Delta MOI\) vuông tại I nên M, O, I thuộc đường tròn đường kính MO

\(\Rightarrow I,A,M,D\) cùng thuộc đường tròn đường kính MO

Hay đường tròn ngoại tiếp MAD đi qua I

d.

Kẻ tiếp tuyến tại B và C của (O) cắt nhau tại P

\(\Rightarrow\) Các tam giác PBO và PCO vuông nên P, B, C, O thuộc đường tròn đường kính OP (1)

Mặt khác OI đi qua trung điểm BC \(\Rightarrow OI\) là trung trực BC

\(PB=PC\) (hai tiếp tuyến cắt nhau), \(OB=OC=R\) nên OP là trung trực BC

\(\Rightarrow P,O,I\) thẳng hàng hay P nằm trên OI (2)

Từ câu b ta có \(\Delta MHB\sim\Delta MCO\Rightarrow\widehat{MCO}=\widehat{MHB}\)

Mà \(\widehat{MHB}+\widehat{BHO}=180^0\Rightarrow\widehat{MCO}+\widehat{BHO}=180^0\)

\(\Rightarrow BCOH\) nội tiếp hay 4 điểm B, C, O, H cùng thuộc 1 đường tròn (3)

(1);(3) \(\Rightarrow P,C,O,B,H\) cùng thuộc đường tròn đường kính PO

\(\Rightarrow\widehat{PHO}\) là góc nt chắn nửa đường tròn (do PO là đường kính) 

\(\Rightarrow PH\perp OM\)

Mà \(AD\perp OM\) hay \(AH\perp OM\) theo giả thiết 

\(\Rightarrow\) Đường thẳng PH trùng đường thẳng AD, hay P nằm trên đường thẳng AD (4)

(2);(4) \(\Rightarrow P\) là giao điểm của OI và AD

\(\Rightarrow P\) trùng Q

\(\Rightarrow Q\) là giao điểm 2 tiếp tuyến tại B và C

Hay QB, QC là tiếp tuyến của (O)