Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$51:32:72=\frac{51}{32\times 72}=\frac{17\times 3}{32\times 3\times 24}=\frac{17}{32\times 24}=\frac{17}{768}$
44444444444444444444444455555555555555555555555555544444444444444444444444445555555555555555555555554444445555555555555555555554444444444455555555555555555554444444444444444444444555555555555555555555444444444444444455555555555555555555544444444444445555555544444445555554444445555545554545454545454545545454545454545454545454545454545454545444444455555544444545444444444444444444444444444444444444444444444455555555555555555555555554444444444444444444444444444444444444444444444444444444555555555555555555555555555555555


Lúc đầu anh trai nhiều hơn em trai số quả bóng là:
13 + 13 = 26 (quả)
Đ/s: 26 quả bóng

a: \(\dfrac{8}{9}=1-\dfrac{1}{9}\)
\(\dfrac{108}{109}=1-\dfrac{1}{109}\)
Vì 9<109 nên \(\dfrac{1}{9}>\dfrac{1}{109}\)
=>\(-\dfrac{1}{9}< -\dfrac{1}{109}\)
=>\(-\dfrac{1}{9}+1< -\dfrac{1}{109}+1\)
=>\(\dfrac{8}{9}< \dfrac{108}{109}\)
b: \(\dfrac{97}{100}=0,97;\dfrac{98}{99}=0,\left(98\right)\)
mà 0,97<0,(98)
nên \(\dfrac{97}{100}< \dfrac{98}{99}\)
c: \(\dfrac{19}{18}=1+\dfrac{1}{18}\)
\(\dfrac{2021}{2020}=1+\dfrac{1}{2020}\)
Vì 18<2020 nên \(\dfrac{1}{18}>\dfrac{1}{2020}\)
=>\(1+\dfrac{1}{18}>1+\dfrac{1}{2020}\)
=>\(\dfrac{19}{18}>\dfrac{2021}{2020}\)
d: \(\dfrac{131}{171}=\dfrac{130+1}{170+1}>\dfrac{130}{170}=\dfrac{13}{17}\)

Bài 1:
a; \(\dfrac{1}{n}\); \(\dfrac{1}{n+1}\) (n > 0; n \(\in\) Z)
\(\dfrac{1}{n}\) - \(\dfrac{1}{n+1}\) = \(\dfrac{n+1-1}{n.\left(n+1\right)}\) = \(\dfrac{1}{n\cdot\left(n+1\right)}\)
⇒ \(\dfrac{1}{n}\) - \(\dfrac{1}{n+1}\) = \(\dfrac{1}{n\left(n+1\right)}\) (đpcm)
Bài 1b
A = \(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\) + \(\dfrac{1}{4.5}\) + \(\dfrac{1}{5.6}\) + \(\dfrac{1}{6.7}\) + \(\dfrac{1}{7.8}\) + \(\dfrac{1}{8.9}\)
A = \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) +\(\dfrac{1}{5}\) - \(\dfrac{1}{6}\) + \(\dfrac{1}{6}\) - \(\dfrac{1}{7}\) + \(\dfrac{1}{7}\) - \(\dfrac{1}{8}\) + \(\dfrac{1}{8}\) - \(\dfrac{1}{9}\)
A = \(\dfrac{1}{2}\) - \(\dfrac{1}{9}\)
A = \(\dfrac{7}{18}\)

Gọi số nhãn vở của Chi là x(nhãn)
(Điều kiện: \(x\in Z^+\))
Trung bình cộng số nhãn vở của 3 bạn là \(\dfrac{x+20+20}{3}=\dfrac{x+40}{3}\)
Chi có số nhãn vở ít hơn trung bình cộng của 3 bạn là 6 cái nên ta có:
\(\dfrac{x+40}{3}-x=6\)
=>\(\dfrac{x+40-3x}{3}=6\)
=>-2x+40=18
=>-2x=-22
=>x=11(nhận)
Vậy: Chi có 11 nhãn vở
Gọi số nhãn vở của Chi là \(x\) (nhãn) (\(x\inℕ^∗\))
Ta có: Trung bình cộng số nhãn vở của 3 bạn là:
\(\dfrac{x+20+20}{3}=\dfrac{x+40}{3}\)
Vì Chi có số nhãn vở ít hơn trung bình cộng của ba bạn 6 cái nên:
\(x-\dfrac{x+40}{3}=6\)
\(3x-\left(x+40\right)=18\)
\(2x-40=18\)
\(2x=58\)
\(x=29\) (nhãn) (thỏa mãn điều kiện)
Vậy Chi có \(29\) nhãn vở.

a: \(-\dfrac{4}{15}=\dfrac{3}{5}-\dfrac{13}{15}=\dfrac{3}{5}+\left(-\dfrac{13}{15}\right)\)
b: \(-\dfrac{4}{15}=\dfrac{-2}{5}\cdot\dfrac{2}{3}\)
c: \(-\dfrac{4}{15}=\dfrac{-2}{5}\cdot\dfrac{2}{3}=\dfrac{-2}{5}:\dfrac{3}{2}\)
 giup em bai em cam on
giup em bai em cam on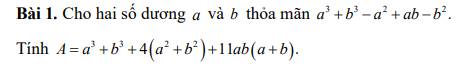

 giup em bai nay em cảm ơn ạ
giup em bai nay em cảm ơn ạ
Ta có: \(E=\dfrac{1}{3}+\dfrac{2}{3^2}+\dfrac{3}{3^3}+...+\dfrac{100}{3^{100}}\)
\(3E=1+\dfrac{2}{3}+\dfrac{3}{3^2}+...+\dfrac{100}{3^{99}}\)
\(3E-E=\left(1+\dfrac{2}{3}+\dfrac{3}{3^2}+..+\dfrac{100}{3^{99}}\right)-\left(\dfrac{1}{3}+\dfrac{2}{3^2}+\dfrac{3}{3^3}+...+\dfrac{100}{3^{100}}\right)\)
\(2E=1+\dfrac{1}{3}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}-\dfrac{100}{3^{100}}\)
\(6E=3+1+\dfrac{1}{3^2}+...+\dfrac{1}{3^{98}}-\dfrac{100}{3^{99}}\)
\(6E-2E=\left(3+1+\dfrac{1}{3^2}+...+\dfrac{1}{3^{98}}-\dfrac{100}{3^{99}}\right)-\left(1+\dfrac{1}{3}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}-\dfrac{100}{3^{100}}\right)\)
\(4E=3-\dfrac{100}{3^{99}}-\dfrac{100}{3^{100}}\)
\(\Rightarrow E=\dfrac{3-\dfrac{100}{3^{99}}-\dfrac{100}{3^{100}}}{4}=\dfrac{3}{4}-\dfrac{\dfrac{100}{3^{99}}+\dfrac{100}{3^{100}}}{4}< \dfrac{3}{4}\) (đpcm)