Chứng minh A = ( a + b – c) – 2 ( a – 2b – c) + a – c chia hết cho 5.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$(9-x)+(-43+22)=-8$
$9-x-43+22=-8$
$31-x-43=-8$
$31-x=43-8=35$
$x=31-35=-4$

51 - 14 \(\times\) (\(x\) + 2) = 359
14 \(\times\) (\(x\) + 2) = 51 - 359
14 \(\times\) (\(x\) + 2) = -308
\(x+2\) = -308 : 14
\(x\) + 2 = -22
\(x\) = - 22 - 2
\(x\) = - 24

⇒ (8x + 3) ⋮ (6x + 1)
⇒ 3(8x + 3) ⋮ (6x + 1)
⇒ (24x + 9) ⋮ (6x + 1)
Ta có:
24x + 9 = 24x + 4 + 5 = 4(6x + 1) + 5
Để (8x + 3) ⋮ (6x + 1) thì 5 ⋮ (6x + 1)
⇒ 6x + 1 ∈ Ư(5) = {-5; -1; 1; 5}
⇒ 6x ∈ {-6; -2; 0; 4}
⇒ x ∈ {-1; -1/3; 0; 2/3}
Nếu x là số nguyên thì x ∈ {-1; 0}

Lời giải:
Hiển nhiên $x$ chẵn.
Số số hạng: $(x-2):2+1=\frac{x}{2}$ (số)
Nếu $x$ hết cho 4:
$(-2)+4+(-6)+8+...+x=2014$
$[(-2)+4]+[(-6)+8]+...+[-(x-2)+x]=2014$
$2+2+.....+2=2014$
Số lần xuất hiện của 2: $\frac{x}{2}:2=\frac{x}{4}$
$\Rightarrow 2.\frac{x}{4}=2014$
$\Rightarrow x=4028$
Nếu $x$ chia $4$ dư $2$ thì theo quy luật $x$ là số âm. Đặt $x=-a$ với $a>0$
$(-2)+4+(-6)+8+.....+(-a)=2014$
$[(-2)+4]+[(-6)+8]+...+[-(a-4)+a-2]+(-a)=2014$
$2+2+....+2+(-a)=2014$
Số lần xuất hiện của 2: $\frac{a-2-2}{2}+1=\frac{a-2}{2}$
$2.\frac{a-2}{2}+(-a)=2014$
$a-2+(-a)=2014$
$-2=2014$ (vô lý)
Vậy $x=4028$

a, A= x + (-37) - 235 = (-11) + (-37) - 235 = -48 - 235 = -283
b, A = x + (-37) - 235 = 187 - 37 - 235 = 150 - 235 = -85

Lời giải:
$xy+5x-6y=35$
$\Rightarrow x(y+5)-6(y+5)=5$
$\Rightarrow (y+5)(x-6)=5$
Do $x,y$ là số nguyên nên $x-6, y+5$ cũng là số nguyên. Mà tích của chúng bằng $5$ nên ta có các TH sau:
TH1: $x-6=1, y+5=5\Rightarrow x=7; y=0$
TH2: $x-6=-1, y+5=-5\Rightarrow x=5; y=-10$
TH3: $x-6=5; y+5=1\Rightarrow x=11; y=-4$
TH4: $x-6=-5; y+5=-1\Rightarrow x=1; y=-6$
Vậy có 4 cặp giá trị x,y thỏa mãn.

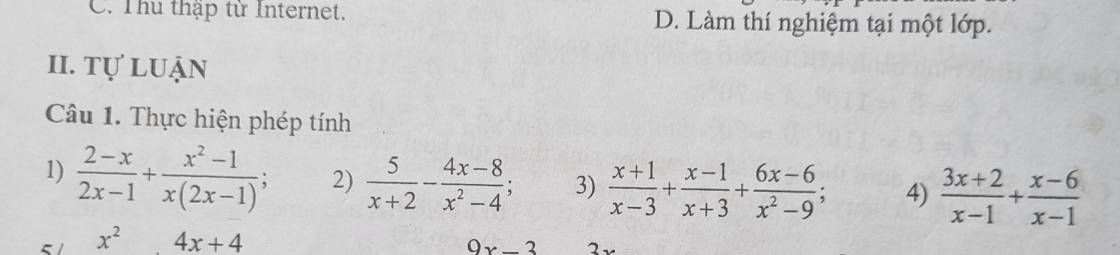
\(A=a+b-c-2a+4b+2c+a-c=\)
\(=5b⋮5\)