\(\dfrac{1}{\left|x-2y\right|}\) + |\(x\) + 2y| = 4

Hay \(\dfrac{1}{\left|x-2y\right|+\left|x+2y\right|}\) = 4 vậy em nhỉ

\(13+\dfrac{x}{20}\text{=}\dfrac{3}{4}\)

\(\dfrac{x}{20}\text{=}\dfrac{3}{4}-13\)

Em xem lại đề nhé tại vì lớp 5 chưa học số âm ạ.

Hoặc đây có thể là đề bài bạn cần.

\(\dfrac{13+x}{20}\text{=}\dfrac{3}{4}\)

\(13+x\text{=}\dfrac{3}{4}\times20\)

\(13+x\text{=}15\)

\(x\text{=}15-13\)

\(x\text{=}2\)

G/s số cần tìm là : x 

Theo bài ra ta có :

\(\dfrac{17+x}{24}\text{=}\dfrac{5}{6}\)

\(6\times\left(17+x\right)\text{=}24\times5\)

\(102+6x\text{=}120\)

\(6x\text{=}120-102\)

\(6x\text{=}18\)

\(x\text{=}3\)

Vậy số tự nhiên cần tìm là : 3.

\(\dfrac{5}{6}\) = \(\dfrac{5\times4}{6\times4}\) = \(\dfrac{20}{24}\) 

Vậy Khi giữ nguyên mẫu số thì số cần thêm vào tử số là: 20 - 17 = 3

Đáp số: 3 

\(\left(3-\dfrac{1}{2}\right)^3-\dfrac{5^4}{25}+\left[\left(\dfrac{1}{2}\right)^2\right]^3\)

\(=\left(\dfrac{5}{2}\right)^3-\dfrac{5^4}{5^2}+\left[\left(\dfrac{1}{2}\right)^2\right]^3\)

\(=\left(\dfrac{5}{2}\right)^3+\left[\left(\dfrac{1}{2}\right)^2\right]^3-5\)

\(=\left(\dfrac{5}{2}+\dfrac{1}{2}\right)\left[\left(\dfrac{5}{2}\right)^2-\dfrac{5}{2}.\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2\right]-5\)

\(=3\left[\dfrac{25}{4}+\dfrac{1}{4}-\dfrac{5}{4}\right]-5\)

\(=3.\dfrac{21}{4}-5\)

\(=\dfrac{63}{4}-5=\dfrac{43}{4}\)

Đính chính \(\dfrac{5^4}{5^2}=25\)

\(...=\dfrac{63}{4}-25=-\dfrac{37}{4}\)

Con ghi rõ đề ra hi

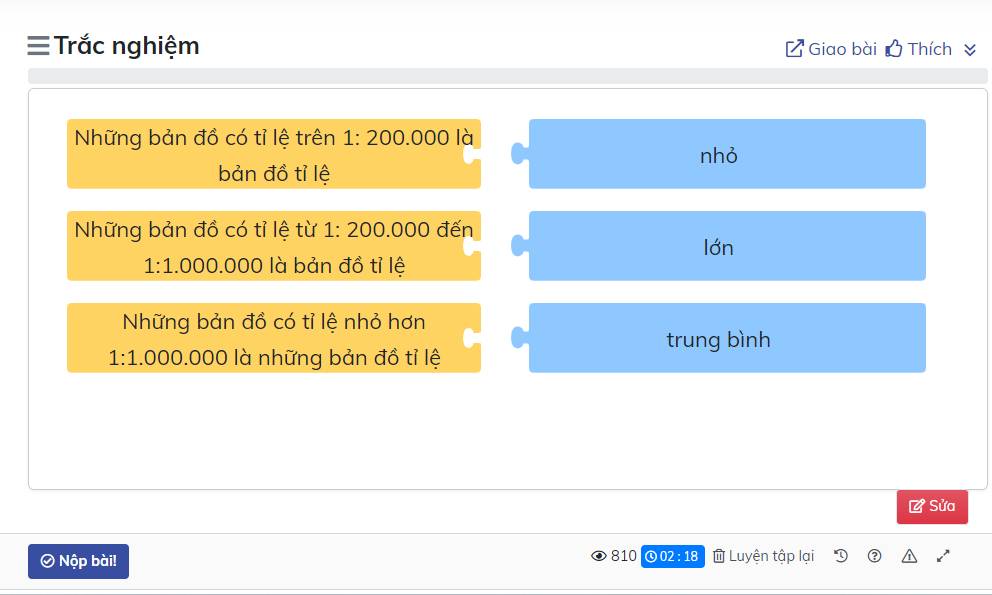
 Với những bản đồ mà tỉ lệ bản đồ có dạng: \(\dfrac{1}{M}\) thì bản đồ tỉ lệ lớn khi M càng nhỏ và ngược lại. Ta có:

Bản đồ có tỉ lệ nhỏ hơn 1: 1 000 000 tức là mẫu số lớn hơn 1000 000 Vậy bản đồ có tỉ lệ nhỏ hơn 1: 1000 000 là những bản đồ có tỉ lệ nhỏ.

Bản đồ có tỉ lệ từ: 1 : 200 000 đến 1: 1000 000 là bản đồ có tỉ lệ trung bình.

Bản đồ có tỉ lệ trên 1: 200 000 tức là mẫu nhỏ hơn 200 000 mà mẫu càng nhỏ thì đó là bản đồ tỉ lệ lớn giờ em đã hiểu rồi đó. 

\(5\dfrac{2}{5}+3\dfrac{2}{3}\text{=}\dfrac{27}{5}+\dfrac{11}{3}\text{=}\dfrac{81}{15}+\dfrac{55}{15}\text{=}\dfrac{136}{15}\)

a, Không có số nào thoả mãn 

b, Bất kì số tự nhiên nào

c, 4 hoặc 7

d, Không có số nào thoả mãn