Hình nào vậy bạn

jxkf9utefrttgt

b) Ta đã chứng minh được tứ giác BCNM là hình thang cân, suy ra N là trung điểm của đáy BC.

câu b nha

a) Ta thấy đa thức \(f\left(x\right)=4x^2+81\) vô nghiệm (*).

 Giả sử \(f\left(x\right)\) có thể phân tích được thành nhân tử, khi đó \(f\left(x\right)=\left(ax+b\right)\left(cx+d\right)\), suy ra \(f\) có nghiệm là \(x=-\dfrac{b}{a}\) hoặc \(x=-\dfrac{d}{c}\), mâu thuẫn với (*).

 Vậy ta không thể phân tích \(f\left(x\right)\) thành nhân tử.

b) \(g\left(x\right)=x^7+x^2+1\)

\(g\left(x\right)=x^7-x+x^2+x+1\)

\(g\left(x\right)=x\left(x^6-1\right)+\left(x^2+x+1\right)\)

\(g\left(x\right)=x\left(x^3-1\right)\left(x^3+1\right)+\left(x^2+x+1\right)\)

\(g\left(x\right)=x\left(x^3+1\right)\left(x-1\right)\left(x^2+x+1\right)+\left(x^2+x+1\right)\)

\(g\left(x\right)=\left(x^2+x+1\right)\left(x^5-x^4+x^2-x+1\right)\)

 Xét \(h\left(x\right)=x^5-x^4+x^2-x+1\), nếu \(h\left(x\right)\) phân tích được thành nhân tử thì nó có nghiệm hữu tỉ. Khi đó nó có dạng \(x=\dfrac{p}{q},\left(p,q\inℤ;\left(p,q\right)=1\right),p|1,q|1\) \(\Rightarrow x=\pm1\). Ta thấy \(h\left(1\right).h\left(-1\right)\ne0\) nên 2 nghiệm này không thỏa mãn. Vậy h(x) không có nghiệm hữu tỉ \(\Rightarrow\) g(x) không thể phân tích tiếp.

a)

\(4x^2+81\\=(2x)^2+2\cdot2x\cdot9+9^2-36x\\=(2x+9)^2-36x\)

Bạn xem lại đề bài nhé!

b)

\(x^7+x^2+1\\=(x^7+x^6+x^5)-x^6-x^5-x^4+(x^4+x^3+x^2)-(x^3-1)\\=x^5(x^2+x+1)-x^4(x^2+x+1)+x^2(x^2+x+1)-(x-1)(x^2+x+1)\\=(x^2+x+1)(x^4-x^4+x^2-x+1)\)

a) \(x=-2\Rightarrow A=\dfrac{4}{\left(-2\right)^2+\left(-2\right)+1}=\dfrac{4}{3}\)

b) \(A=B+C\Rightarrow C=A-B\)

\(=\dfrac{4}{x^2+x+1}-\left(\dfrac{2}{1-x}+\dfrac{2x^2+4x}{x^3-1}\right)\)

\(=\dfrac{4}{x^2+x+1}-\dfrac{2}{1-x}-\dfrac{2x^2+4x}{x^3-1}\)

\(=\dfrac{4}{x^2+x+1}+\dfrac{2}{x-1}-\dfrac{2x^2+4x}{\left(x-1\right)\left(x^2+x+1\right)}\)

\(=\dfrac{4\left(x-1\right)+2\left(x^2+x+1\right)-2x^2-4x}{\left(x-1\right)\left(x^2+x+1\right)}\)

\(=\dfrac{4x-4+2x^2+2x+2-2x^2-4x}{\left(x-1\right)\left(x^2+x+1\right)}\)

\(=\dfrac{2x-2}{\left(x-1\right)\left(x^2+x+1\right)}\)

\(=\dfrac{2\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)

\(=\dfrac{2}{x^2+x+1}\)

Vậy \(C=\dfrac{2}{x^2+x+1}\)

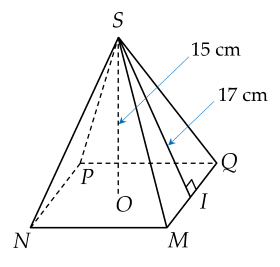
\(V_{S.MNPQ}=\dfrac{1}{3}.S_{MNPQ}.SO\)

\(\Rightarrow S_{MNPQ}=\dfrac{3.V_{S.MNPQ}}{SO}=\dfrac{3.1280}{15}=256cm^2\)

Xét tg vuông SOI

\(OI=\sqrt{SI^2-SO^2}\) (Pitago)

\(\Rightarrow OI=\sqrt{17^2-15^2}=8cm\)

Ta có

\(OI=\dfrac{MN}{2}\Rightarrow MN=2.OI=2.8=16cm\)

Ta có:

\(V=\dfrac{1}{3}.S_{MNPQ}.15=1280\left(cm^3\right)\)

\(\Rightarrow S_{MNPQ}=\dfrac{1280.3}{15}=256\left(cm^2\right)\)

\(\Rightarrow MN=\sqrt{256}=16\left(cm\right)\)

a) Tứ giác ABCD có:

\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\) (tổng các góc trong tứ giác ABCD)

Gọi \(x,y,z,t\) lần lượt là số đo các góc: \(\widehat{A},\widehat{B},\widehat{C},\widehat{D}\) \(\left(x,y,z,t>0\right)\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\(\dfrac{x}{1}=\dfrac{y}{2}=\dfrac{z}{3}=\dfrac{t}{4}=\dfrac{x+y+z+t}{1+2+3+4}=\dfrac{360^0}{10}=36^0\)

\(\dfrac{y}{2}=36^0\Rightarrow y=2.36^0=72^0\) (nhận)

Vậy \(\widehat{B}=72^0\)

b) Đường chéo của màn hình điện thoại:

\(\sqrt{7^2+15,5^2}\simeq17\left(cm\right)\) \(\simeq17.2,54\simeq43\left(inch\right)\)

Thể tích của khúc gỗ là: 30.30.30 = 27 000 (cm³)

Thể tích của hình chóp từ giác đều là: 30.30.30.1/3 = 9 000 (cm³)

Thể tích của phần gỗ bị cắt đi là: 27 000 - 9 000 = 18 000 (cm³)