Giải:

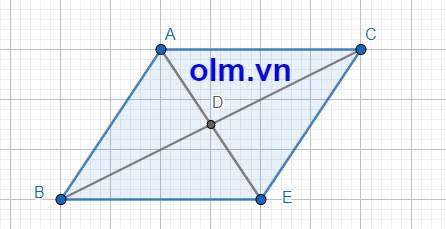
a; Xét tứ giác ABEC có AD = DE (gt); BD = DC (gt)

⇒ tứ  giác ABEC là hình bình hành (tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường thì tứ giác đó là hình bình hành)

⇒ AC = BE 

b; Xét tam giác ABE ta có:

  AB + BE > AE (trong một tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)

BE = AC (cmt)

⇒ AB + AC > AE 

⇒ \(\dfrac{AB+AC}{2}\) > \(\dfrac{AE}{2}\) 

       AD = DE = \(\dfrac{1}{2}\)AE (vì D là trung điểm AE)

⇒\(\dfrac{AB+AC}{2}\) > AD 

a: Xét ΔAMB và ΔEMC có

MA=ME

\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)

MB=MC

Do đó: ΔAMB=ΔEMC

b: Xét ΔMBE và ΔMCA có

MB=MC

\(\widehat{BME}=\widehat{CMA}\)(hai góc đối đỉnh)

ME=MA

Do đó: ΔMBE=ΔMCA

=>\(\widehat{MBE}=\widehat{MCA}\)

=>BE//AC

Đường xiên nào có hình chiếu nhỏ hơn thì nhỏ hơn.

C đúng

C

\(f\left(2\right)-f\left(-1\right)=6\)

\(\Rightarrow\left[\left(a-1\right).2\right]-\left[\left(a-1\right).\left(-1\right)\right]=6\)

\(\Rightarrow3\left(a-1\right)=6\)

\(\Rightarrow a-1=2\)

\(\Rightarrow a=3\)

ĐKXĐ: x>=-1

\(\dfrac{1}{2}\cdot\sqrt{x+1}-\dfrac{4}{3}=\sqrt{\dfrac{36}{49}}\)

=>\(\dfrac{1}{2}\cdot\sqrt{x+1}-\dfrac{4}{3}=\dfrac{6}{7}\)

=>\(\dfrac{1}{2}\cdot\sqrt{x+1}=\dfrac{4}{3}+\dfrac{6}{7}=\dfrac{28}{21}+\dfrac{18}{21}=\dfrac{46}{21}\)

=>\(\sqrt{x+1}=\dfrac{46}{21}\cdot2=\dfrac{92}{21}\)

=>\(x+1=\dfrac{8464}{441}\)

=>\(x=\dfrac{8023}{441}\)(nhận)

Đề thiếu vế phải rồi em

Gọi a (m), b (m), c (m) lần lượt là độ dài ba cạnh của tam giác (a, b, c > 0)

Do độ dài ba cạnh tỉ lệ thuận với 3; 4; 5 nên:

a/3 = b/4 = c/5

Do tổng độ dài cạnh lớn nhất và cạnh nhỏ nhất là 40 m nên:

a + c = 40

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

a/3 = b/4 = c/5 = (a + c)/(3 + 5) = 40/8 = 5

a/3 = 5 ⇒ a = 5.3 = 15 (nhận)

b/4 = 5 ⇒ b = 5.4 = 20 (nhận)

c/5 = 5 ⇒ c = 5.5 = 25 (nhận)

Vậy độ dài ba cạnh của tam giâc cần tìm là: 15 m, 20 m, 25 m

                    Giải:

a; Khi rút ngẫu nhiên một tấm thẻ từ hộp chứa 8 tấm thẻ thì có 8 khả năng có thể xảy ra.

Xét các số 2; 3; 4; 5; 6; 7; 8; 9

Vì các số lẻ thuộc dãy số trên lần lượt là:  3; 5; 7; 9 (có 4 số lẻ)

Nên có 4 kết quả thuận lợi cho biến cố lấy được thẻ là số lẻ.

vậy xác suất của biến cố lấy được thẻ số lẻ là: 4 : 8 = \(\dfrac{1}{2}\)

b; Xét các số 2; 3; 4; 5; 6; 7; 8; 9

Vì các số chẵn thuộc dãy số trên lần lượt là: 2; 4; 6; 8 (có 4 số chẵn)

Nên có 4 kết quả thuận lợi cho biến cố lấy được thẻ là số chẵn.

Vậy xác suất của biến cố lấy được thẻ số chẵn là: 4 : 8 = \(\dfrac{1}{2}\)

c; Xét các số 2; 3; 4; 5; 6; 7; 8; 9

Vì các số nguyên tố thuộc dãy số trên lần lượt là các số: 2; 3; 5; 7 (có 4 số nguyên tố)

Nên có 4 kết quả thuận lợi cho biến cố lấy được thẻ là số chẵn.

Vậy xác suất của biến cố lấy được thẻ số nguyên tố là: 4 : 8 = \(\dfrac{1}{2}\)

Kết luận: a; Xác suất của biến cố lấy được thẻ số lẻ là \(\dfrac{1}{2}\)

               b; Xác suất của biến cố lấy được thẻ là số chẵn là \(\dfrac{1}{2}\)

               c; Xác suất của biến cố lấy được thẻ là số nguyên tố là \(\dfrac{1}{2}\)

a) Có 4 khả năng lấy được số lẻ là: 3; 5; 7; 9

Xác suất của biến cố "lấy được thẻ ghi số lẻ":

\(P=\dfrac{4}{8}=\dfrac{1}{2}\)

b) Có 4 khả năng lấy được thẻ ghi số chẵn là: 2; 4; 6; 8

Xác suất của biến cố "lấy được thẻ ghi số chẵn":

\(P=\dfrac{4}{8}=\dfrac{1}{2}\)

c) Có 4 thẻ ghi số nguyên tố là: 2; 3; 5; 7

Xác suất của biến cố "lấy được thẻ ghi số nguyên tố":

\(P=\dfrac{4}{8}=\dfrac{1}{2}\)