Tìm min P=3x^2+x-2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Lập bảng
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... |
| 7n | 7 | 9 | 3 | 1 | 7 | 9 | 3 | 1 | ... |
| 9n | 9 | 1 | 9 | 1 | 9 | 1 | 9 | 1 | ... |
Ta có: 2018 : 4 = 504 (dư 2)
Suy ra \(2017^{2018}+2019^{2018}= \overline{...9}+\overline{...1}=\overline{...0}\)
Vậy 20172018 + 20192018 chia hết cho 10
b) Làm tương tự như câu a)

\(\left(x-5\right)^{2020}+\left(y-x+1\right)^{2022}=0\left(1\right)\)
Ta có \(\left\{{}\begin{matrix}\left(x-5\right)^{2020}\ge0,\forall x\\\left(y-x+1\right)^{2022}\ge0,\forall x;y\end{matrix}\right.\)
\(\left(1\right)\Rightarrow\left\{{}\begin{matrix}\left(x-5\right)^{2020}=0\\\left(y-x+1\right)^{2022}=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x-5=0\\y-x+1=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=5\\y-5+1=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=5\\y=4\end{matrix}\right.\)
( 2x - 5 )2020 + ( 5y + 1 )2022 ≤ 0
Ta có : ( 2x - 5 )2020 ≥ 0 ∀ x
( 5y + 1 )2022 ≥ 0 ∀ y
=> ( 2x - 5 )2 + ( 5y + 1 )2022 ≥ 0 ∀ x, y
Kết hợp với đề bài => Chỉ xảy ra trường hợp ( 2x - 5 )2020 + ( 5y + 1 )2022 = 0
Khi đó \hept{2�−5=05�+1=0⇔\hept{�=52�=−15\hept{2x−5=05y+1=0⇔\hept{x=25y=−51

\(A=\dfrac{6}{1\cdot4}+\dfrac{6}{4\cdot7}+...+\dfrac{6}{46\cdot49}\\ =2\cdot\left(\dfrac{3}{1\cdot4}+\dfrac{3}{4\cdot7}+...+\dfrac{3}{46\cdot49}\right)\\=2\cdot\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{46}-\dfrac{1}{49}\right)\\ =2\cdot\left(1-\dfrac{1}{49}\right)\\ =\dfrac{96}{49}\)


\(\dfrac{3^6.45^4-15^{13}.5^{-9}}{27^4.25^3+45^6}=\dfrac{3^6.3^85^4-3^{13}.5^{13}.5^{-9}}{3^{12}.5^6+3^{12}.5^6}\)
\(=\dfrac{3^{14}.5^4-3^{13}.5^4}{2.3^{12}.5^6}=\dfrac{3^{13}.5^4\left(3-1\right)}{2.3^{12}.5^6}\)
\(=\dfrac{3.2}{2.5^2}=\dfrac{3}{25}\)
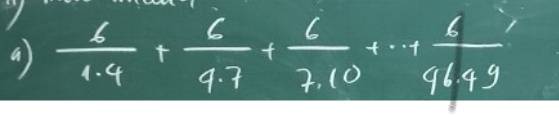


\(P=3x^2+x-2=3\left(x^2+\dfrac{1}{3}x+\dfrac{1}{9}\right)-\dfrac{5}{3}=3\left(x+\dfrac{1}{3}\right)^2-\dfrac{5}{3}\\ Vì:\left(x+\dfrac{1}{3}\right)^2\ge0\forall x\in R\\ Vậy:3\left(x+\dfrac{1}{3}\right)^2-\dfrac{5}{3}\ge\dfrac{5}{3}\forall x\in R\\ Vậy:min_P=\dfrac{5}{3}.khi.x=-\dfrac{1}{3}\)