
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔBDE vuông tại D và ΔDCE vuông tại C có
\(\widehat{BED}\) chung
do đó: ΔBDE~ΔDCE
b:
Ta có: CH\(\perp\)DE
DB\(\perp\)DE
Do đó: CH//DB
Xét ΔHCD vuông tại H và ΔCDB vuông tại C có
\(\widehat{HCD}=\widehat{CDB}\)(HC//DB)
Do đó: ΔHCD~ΔCDB
=>\(\dfrac{HC}{CD}=\dfrac{CD}{DB}\)
=>\(CD^2=HC\cdot DB\)
c: Ta có: ABCD là hình chữ nhật
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
=>OB=OD(1)
Xét ΔEOD có HK//OD
nên \(\dfrac{HK}{OD}=\dfrac{EK}{EO}\left(2\right)\)
Xét ΔEOB có KC//OB
nên \(\dfrac{KC}{OB}=\dfrac{EH}{EO}\left(3\right)\)
Từ (1),(2),(3) suy ra KH=KC
=>K là trung điểm của HC

a: Chu vi đáy là 2x3=6(m)
Diện tích xung quanh là \(6\cdot3=18\left(m^2\right)\)
b: Diện tích cần sơn là \(18\cdot3=54\left(m^2\right)\)
Số tiền phải trả là \(54\cdot30000=1620000\left(đồng\right)\)

a) Xác suất thực nghiệm của biến cố mặt xuất hiện của đồng xu là mặt N là:
\(8:20=\dfrac{8}{20}=\dfrac{2}{5}\)
Vậy xác suất thực nghiệm của biến cố mặt xuất hiện của đồng xu là mặt N là \(\dfrac{2}{5}\).
b) Số lần xuất hiện mặt N là:
\(15-9=6\) ( lần )
Xác suất thực nghiệm của biến cố mặt xuất hiện của đồng xu là mặt N là:
\(6:15=\dfrac{6}{15}=\dfrac{2}{5}\)
Vậy xác suất thực nghiệm của biến cố mặt xuất hiện của đồng xu là mặt N là \(\dfrac{2}{5}\).
a) Xác suất thực nghiệm của biến cố xuất hiện mặt N:
P = 8/20 = 2/5
b) Xác suất thực nghiệm của biến cố xuất hiện mặt S:
P = 9/15 = 3/5

a) Đồ thi của hàm số đi qua điểm \(B\left(3;-2\right)\) thay các giá trị x và y tương ứng vào ta có:
\(-2=\left(2m-1\right)\cdot3+1\)
\(\Leftrightarrow3\left(2m-1\right)=-3\)
\(\Leftrightarrow2m-1=-1\)
\(\Leftrightarrow2m=0\)
\(\Leftrightarrow m=0\left(tm\right)\)
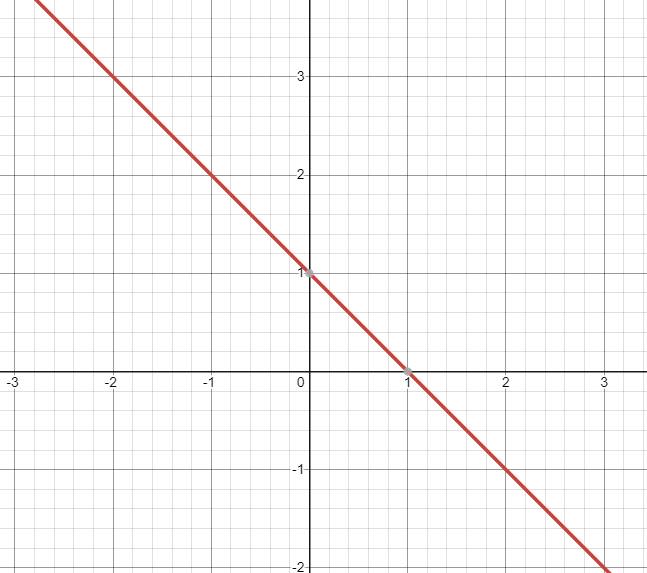
b) Với `m=0` thì ta có hàm số: \(y=\left(2\cdot0-1\right)x+1\Rightarrow y=-x+1\)
Vẽ:

1) \(7-5x=5\left(3-x\right)\)
\(\Leftrightarrow7-5x=15-5x\)
\(\Leftrightarrow-5x+5x=15-7\)
\(\Leftrightarrow0=8\) (vô lý)
Phương trình vô nghiệm
2) \(\dfrac{x+3}{2}-\dfrac{x-1}{3}=\dfrac{x+5}{6}+1\)
\(\Leftrightarrow\dfrac{3\left(x+3\right)}{6}-\dfrac{2\left(x-1\right)}{6}=\dfrac{x+5}{6}+\dfrac{6}{6}\)
\(\Leftrightarrow3\left(x+3\right)-2\left(x-1\right)=x+5+6\)
\(\Leftrightarrow3x+9-2x+2=x+11\)
\(\Leftrightarrow x+11=x+11\)
\(\Leftrightarrow x-x=11-11\)
\(\Leftrightarrow0=0\) (luôn đúng)
Vậy phương trình có vô số nghiệm

Gọi chiều rộng là x(m)
(ĐIều kiện: x>0)
NỬa chu vi miếng đất là 60:2=30(m)
Chiều dài miếng đất là 30-x(m)
Bốn lần chiều rộng bằng 2 lần chiều dài nên ta có:
4x=2(30-x)
=>4x=60-2x
=>6x=60
=>x=10(nhận)
Vậy: Chiều rộng là 10m; chiều dài là 30-10=20m
Diện tích miếng đất là \(10\cdot20=200\left(m^2\right)\)

Xét ΔABC có
M,N lần lượt là trung điểm của BC,BA
=>MN là đường trung bình của ΔABC
=>MN//AC
=>MN\(\perp\)AB tại N
Xét ΔINB vuông tại N và ΔIBM vuông tại B có
\(\widehat{NIB}\) chung
Do đó: ΔINB~ΔIBM
=>\(\dfrac{IN}{IB}=\dfrac{IB}{IM}\)
=>\(IN\cdot IM=IB^2\)




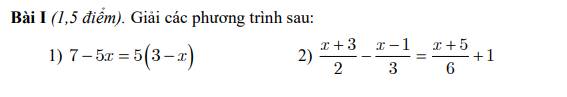
Câu 2: \(\dfrac{x}{6}+\dfrac{y}{8}=1\)
=>\(\dfrac{4x+3y}{24}=1\)
=>4x+3y=24
=>4x+3y-24=0
Khoảng cách từ O đến đường thẳng 4x+3y-24=0 là:
\(d\left(O;4x+3y-24=0\right)=\dfrac{\left|0\cdot4+0\cdot3-24\right|}{\sqrt{3^2+4^2}}=\dfrac{24}{5}=4,8\)