1 ô tô đi từ A đến B . cùng lúc đó có một ô tô đi từ B về A gặp ô tô thứ nhất từ cách điểm A là 140 km biết ô tô đi từ A đến B mất 8 giờ và ô tô thứ 2 đi từ B về A mất 7 giờ . tính quãng đường AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


y + y : 0,25 + y: 0,5 + y: 0,125 = 0,6
y x 1 + y x 4 + y x 2 + y x 8 = 0,6
y x (1 + 4 + 2 + 8) = 0,6
y x (5 + 2 + 8) = 0,6
y x (7 + 8) = 0,6
y x 15 = 0,6
y = 0,6 : 15
y = 0,04

a: \(56\times89-46\times89\)
\(=89\times\left(56-46\right)\)
\(=89\times10=890\)
b: 700+197-200+203
=500+(197+203)
=500+400
=900
a) 56 x 89 - 46 x 89
= (56 x 89 - 46 x 8)
= (56 - 46) x 89
= 10 x 89
= 890
b) 700 + 197 - 200 + 203
= (700 - 200) + (197 + 203)
= 500 + 400
= 900
Tick cho tớ với ạ


Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!
HGSDFTFRYTETTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTT

Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!

Đổi 2 giờ 30 phút = 2,5 giờ
Chú rùa đi được số kilomet là:
\(0,5\times2,5=1,25\left(km\right)\)
Đáp số:

Olm chào em đây là toán nâng cao chuyên đề cho giá trị của một số phần tìm giá trị của một phần như thế, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
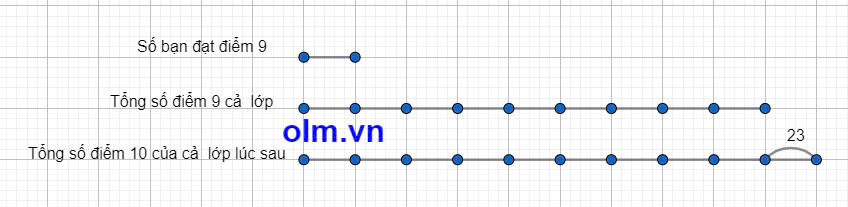
Giả sử số bạn đạt điểm 10 thêm vào 4 bạn thì khi đó số bạn điểm 9 bằng số bạn đạt điểm 10, tổng số điểm 10 của cả lớp hơn tổng số điểm 9 của cả lớp là:
10 x 4 - 17 = 23(điểm)
Coi số bạn được 9 điểm của lớp là 1 phần thì ta có sơ đồ:
Theo sơ đồ ta có:
Số bạn đạt điểm 9 là:
23:(10 - 9) = 23 (bạn)
Số bạn đạt điểm 10 là:
23 - 4 = 19 (bạn)
Đáp số: Số bạn đạt điểm 9 là: 23 bạn
Số bạn đạt điểm 10 là: 19 bạn

Đây là toán nâng cao chuyên đề chuyển động ngược chiều, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng đơn vị quy ước như sau:
(sử dụng quãng đường AB là đơn vị quy ước0
Giải:
Cứ mỗi giờ xe A đi được: 1 : 8 = \(\frac18\)(quãng đường AB)
Cứ mỗi giờ xe B đi được: 1 : 7 = \(\frac17\) (quãng đường AB)
Thời gian hai xe gặp nhau là: 1 : (\(\frac18+\frac17\)) = \(\frac{56}{15}\) (giờ)
Vận tốc xe A là: 140 : \(\frac{56}{15}\) = 37,5 (km/h)
Quãng đường AB dài là: 37,5 x 8 = 300 (km)
Đáp số: 300km
Đây là toán nâng cao chuyên đề chuyển động ngược chiều, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, VIOEDU-trợ lí học tập sẽ hướng dẫn các em giải chi tiết dạng này bằng đơn vị quy ước như sau:
(sử dụng quãng đường AB là đơn vị quy ước0
Giải:
Cứ mỗi giờ xe A đi được: 1 : 8 = \(\frac{1}{8}\)(quãng đường AB)
Cứ mỗi giờ xe B đi được: 1 : 7 = \(\frac{1}{7}\) (quãng đường AB)
Thời gian hai xe gặp nhau là: 1 : (\(\frac{1}{8} + \frac{1}{7}\)) = \(\frac{56}{15}\) (giờ)
Vận tốc xe A là: 140 : \(\frac{56}{15}\) = 37,5 (km/h)
Quãng đường AB dài là: 37,5 x 8 = 300 (km)
Đáp số: 300km
chúc các bạn học tốt