A B C M N D

a/

Xét tứ giác BMCD có

NB=NC (gt)

ND=NM (gt)

=> BMCD là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)

b/

Để BMCD là hình thoi \(\Rightarrow MD\perp BC\) (Hình thoi có 2 đường chéo vuông góc) (1)

Ta có

MA=MC (gt)

NB=NC (gt)

=> MN là đường trung bình của tg ABC => MN//AB => MD//AB (2)

Từ (1) và (2) \(\Rightarrow AB\perp BC\)

Để BMCD là hình thoi => tg ABC là tg vuông tại B

a) Tứ giác BMCD có:

N là trung điểm của BC (gt)

N là trung điểm của DM (gt)

\(\Rightarrow\) BMCD là hình bình hành

b) Để BMCD là hình thoi thì \(BC\perp DM\)

Ta có:

M là trung điểm của AC (gt)

N là trung điểm của BC (gt)

\(\Rightarrow MN\) là đường trung bình của \(\Delta ABC\)

\(\Rightarrow MN\) // \(AB\)

\(\Rightarrow DM\) // \(AB\)

Mà \(DM\perp BC\)

\(\Rightarrow BC\perp AB\)

Vậy để BMCD là hình thoi thì \(\Delta ABC\) vuông tại B

M N Q P A I K

MN//PQ (cạnh đối hbh) => MI//KQ

Ta có

\(MI=\dfrac{MN}{2};KQ=\dfrac{PQ}{2}\) Mà MN=PQ (cạnh đối hbh) => MI=KQ

=> MIKQ là hbh (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)

b/

Ta có

MA=MQ (gt) (1)

\(MN=2MQ\left(gt\right)\Rightarrow MQ=\dfrac{MN}{2}\) (2)

Ta có

\(MI=\dfrac{MN}{2}\) (3)

Từ (1) (2) (3) \(\Rightarrow MA=MI=\dfrac{MN}{2}\) => tg AMI cân tại M

Ta có

\(\widehat{AMI}=\widehat{AMP}-\widehat{M}=180^o-120^o=60^o\)

Xét tg AMI có

\(\widehat{MAI}+\widehat{MIA}+\widehat{AMI}=180^o\)

\(\Rightarrow\widehat{MAI}+\widehat{MIA}=180^o-\widehat{AMI}=180^o-60^o=120^o\)

Mà \(\widehat{MAI}=\widehat{MIA}\) (góc ở đáy tg cân)

\(\Rightarrow\widehat{MAI}=\widehat{MIA}=\dfrac{120^o}{2}=60^o\)

\(\Rightarrow\widehat{MAI}=\widehat{MIA}=\widehat{AMI}=60^o\Rightarrow\Delta AMI\) là tg đều

c/

Xét hbh MNPQ có

MQ//NP => MA//NP

MA=MQ (gt); MQ=NP (cạnh đối hbh)

=> MA=NP

=> APMN là hình bình hành (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)

Ta có

\(MI=AI=\dfrac{MN}{2}\)  (cạnh tg đều)

\(NI=\dfrac{MN}{2}\)

\(\Rightarrow AI=NI=\dfrac{MN}{2}\) => tg AIN cân tại I

Ta có \(\widehat{AIN}=\widehat{MIN}-\widehat{AIM}=180^o-60^o=120^o\)

Xét tg cân AIN có

\(\widehat{AIN}+\widehat{IAN}+\widehat{INA}=180^o\)

\(\Rightarrow\widehat{IAN}+\widehat{INA}=180^o-\widehat{AIN}=180^o-120^o=60^o\)

Mà \(\widehat{IAN}=\widehat{INA}\) (góc ở đáy tg cân)

\(\Rightarrow\widehat{IAN}=\widehat{INA}=\dfrac{60^o}{2}=30^o\)

Xét tg AMN có

\(\widehat{MAN}+\widehat{AMI}+\widehat{INA}=180^o\)

\(\Rightarrow\widehat{MAN}=180^o-\widehat{AMI}-\widehat{INA}=180^o-60^o-30^o=90^o\)

=> APMN là hình chữ nhật (hình bình hành có 1 góc vuông là HCN

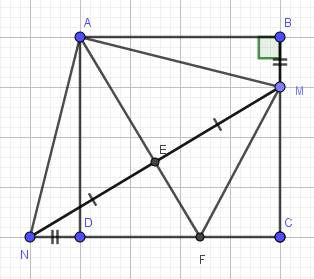
a) Do ABCD là hình vuông (gt)

\(\Rightarrow AB=AD\)

\(\widehat{ABM}=\widehat{ADN}=90^0\)

Xét hai tam giác vuông: \(\Delta ABM\) và \(\Delta ADN\) có:

\(AB=AD\left(cmt\right)\)

\(BM=DN\left(gt\right)\)

\(\Rightarrow\Delta ABM=\Delta ADN\) (hai cạnh góc vuông)

\(\Rightarrow AM=AN\) (hai cạnh tương ứng)

\(\widehat{BAM}=\widehat{DAN}\) (hai góc tương ứng)

Ta có:

\(\widehat{BAM}+\widehat{DAM}=90^0\)

\(\Rightarrow\widehat{DAN}+\widehat{DAM}=90^0\)

\(\Rightarrow\widehat{MAN}=90^0\)

\(\Delta AMN\) có:

\(AM=AN\left(cmt\right)\)

\(\Rightarrow\Delta AMN\) cân tại A

Mà \(\widehat{MAN}=90^0\left(cmt\right)\)

\(\Rightarrow\Delta AMN\) vuông cân tại A

b) Do \(\Delta AMN\) cân tại A

E là trung điểm của MN

\(\Rightarrow AE\) là đường trung tuyến, cũng là đường cao của \(\Delta AMN\)

\(\Rightarrow AE\perp MN\)

\(\Rightarrow EF\perp MN\)

Xét hai tam giác vuông: \(\Delta FEM\) và \(\Delta FEN\) có:

\(EM=EN\left(gt\right)\)

\(EF\) là cạnh chung

\(\Rightarrow\Delta FEM=\Delta FEN\) (hai cạnh góc vuông)

\(\Rightarrow FM=FN\) (hai cạnh tương ứng)

Xét \(\Delta FAN\) và \(\Delta FAM\) có:

\(FA\) là cạnh chung

\(FN=FM\left(cmt\right)\)

\(AN=AM\left(cmt\right)\)

\(\Rightarrow\Delta FAN=\Delta FAM\left(c-c-c\right)\)

Thuận lợi:

1. Lực lượng lao động dồi dào: Dân số đông tạo ra một lực lượng lao động lớn, giúp tăng cường sản xuất và phát triển kinh tế.

2. Thị trường tiêu thụ lớn: Với số lượng người tiêu dùng đông, châu Á có thể tạo ra một thị trường tiêu thụ lớn, thu hút các công ty và doanh nghiệp đầu tư và phát triển.

3. Đa dạng văn hóa và nguồn nhân lực: Dân số đông mang lại sự đa dạng về văn hóa, truyền thống và nguồn nhân lực, tạo điều kiện cho sự phát triển và sáng tạo trong nhiều lĩnh vực.

Khó khăn:

1. Áp lực về tài nguyên: Dân số đông tạo ra áp lực lớn về tài nguyên, đặc biệt là tài nguyên tự nhiên như nước, đất đai và năng lượng. Việc quản lý và sử dụng tài nguyên hiệu quả trở thành một thách thức.

2. Cạnh tranh về việc làm: Với lực lượng lao động đông, cạnh tranh về việc làm trở nên khốc liệt. Điều này có thể dẫn đến tình trạng thất nghiệp và áp lực lớn đối với các chính phủ để tạo ra đủ việc làm cho dân số.

3. Áp lực về hạ tầng và dịch vụ công: Dân số đông đặt áp lực lớn lên hạ tầng và dịch vụ công như giao thông, y tế, giáo dục và cơ sở hạ tầng. Điều này đòi hỏi sự đầu tư lớn và quản lý hiệu quả để đáp ứng nhu cầu của dân số.

4. Vấn đề an ninh và xã hội: Dân số đông có thể tạo ra những vấn đề an ninh và xã hội như tăng cường tội phạm, áp lực về chính trị và xã hội, và khó khăn trong việc quản lý và duy trì trật tự công cộng.

17 chia hết cho x ⇒ x ∈ Ư(17) 

21 chia hết cho x ⇒ x ∈ Ư(21)

51 cũng chia hết cho x ⇒ x ∈ Ư(51)

Mà x là số lớn nhất nên:

x ∈ ƯCLN(17, 21, 51)

Ta có:

\(17=17\)

\(21=3\cdot7\)

\(51=17\cdot3\)

\(\RightarrowƯCLN\left(17,21,51\right)=1\)

Vậy x = 1 

help meee giúp tớ ikkkk

Bài thơ Những cánh buồm của nhà thơ Hoàng Trung Thông là một tác phẩm gợi lên trong em rất nhiều những rung động. Hình ảnh hai cha con trong bài thơ thật ấm áp và thân thiết. Hành động nắm lấy tay con, dắt con đi, rồi mỉm cười xoa đầu con nhỏ của người cha khiến em cảm động vô cùng. Những hành động ấy thật gần gũi và bình dị. Như người cha yêu dấu vẫn thường làm với em. Qua đó, em như cảm nhận được tình cảm ấm áp, yêu thương trìu mến mà người cha dành cho đứa con của mình. Chính ông đã khơi gợi lên những tò mò, thích thú về thế giới xa lạ ngoài kia cho đứa con của mình. Thôi thúc đứa trẻ ấy đứng lên và khám phá những điều mới mẻ. Đó chính là sự bao la của tình cha vĩ đại. Và người con lớn lên trong tình thương ấy, cũng quấn quít và yêu thương cha của mình. Trong suy nghĩ non nớt, đứa trẻ đã mong mỏi mượn của cha cánh buồm trắng để rong ruổi ra khơi. Chính suy nghĩ ấy đã cho thấy sự tin tưởng, kính yêu mà người con dành cho cha mình. Cũng như trong tâm trí em, người cha luôn là mái nhà kiên cố nhất có thể che chắn mọi điều, không nề hà khó khăn. Những rung cảm về tình phụ tử thiêng liêng và ấm áp ấy, đã được bài thơ Những cánh buồm khơi gợi và ấp ủ trong em

Do mức làm của mỗi người như nhau và cùng làm 1 công việc nên số người và số ngày là hai đại lượng tỉ lệ nghịch

Số ngày còn lại:

15 - 5 = 10 (ngày)

Tổng số người sau khi thêm 3 người:

12 + 3 = 15

Số ngày hoàn thành công việc với 15 người:

12 × 10 : 5 = 8 (ngày)

                            Giải: 

 Công việc còn lại 12 người phải làm trong số ngày là:

                  15 - 5 = 10 (ngày)

Công việc còn lại 1 người phải làm trong số ngày là:

                  10 x 12 = 120 (ngày)

Thực tế số người làm công việc còn lại là:

                  12 + 3 = 15 (người)

Để hoàn thành công việc còn lại 15 người phải làm trong số ngày là:

                120 : 15 = 8 (ngày)

                  Đáp số: 8 ngày 

\(12,345=10+2+0,3+0,04+0,005\)

12,345=10+2+0,3+0,04+0,005

`#3107.101107`

`(5x - 1)(2x - 6) = 0`

\(\Rightarrow\left[{}\begin{matrix}5x-1=0\\2x-6=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}5x=1\\2x=6\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=3\end{matrix}\right.\)

Vậy, \(x\in\left\{3;\dfrac{1}{5}\right\}.\)

(5x-1).(2x-6) = 0
5x-1 = 0 hoặc 2x-6 = 0
+) 5x-1 = 0 suy ra x = 0,2
+) 2x-6 = 0 suy ra x = 6
Vậy x = 0,2 ; x = 6.