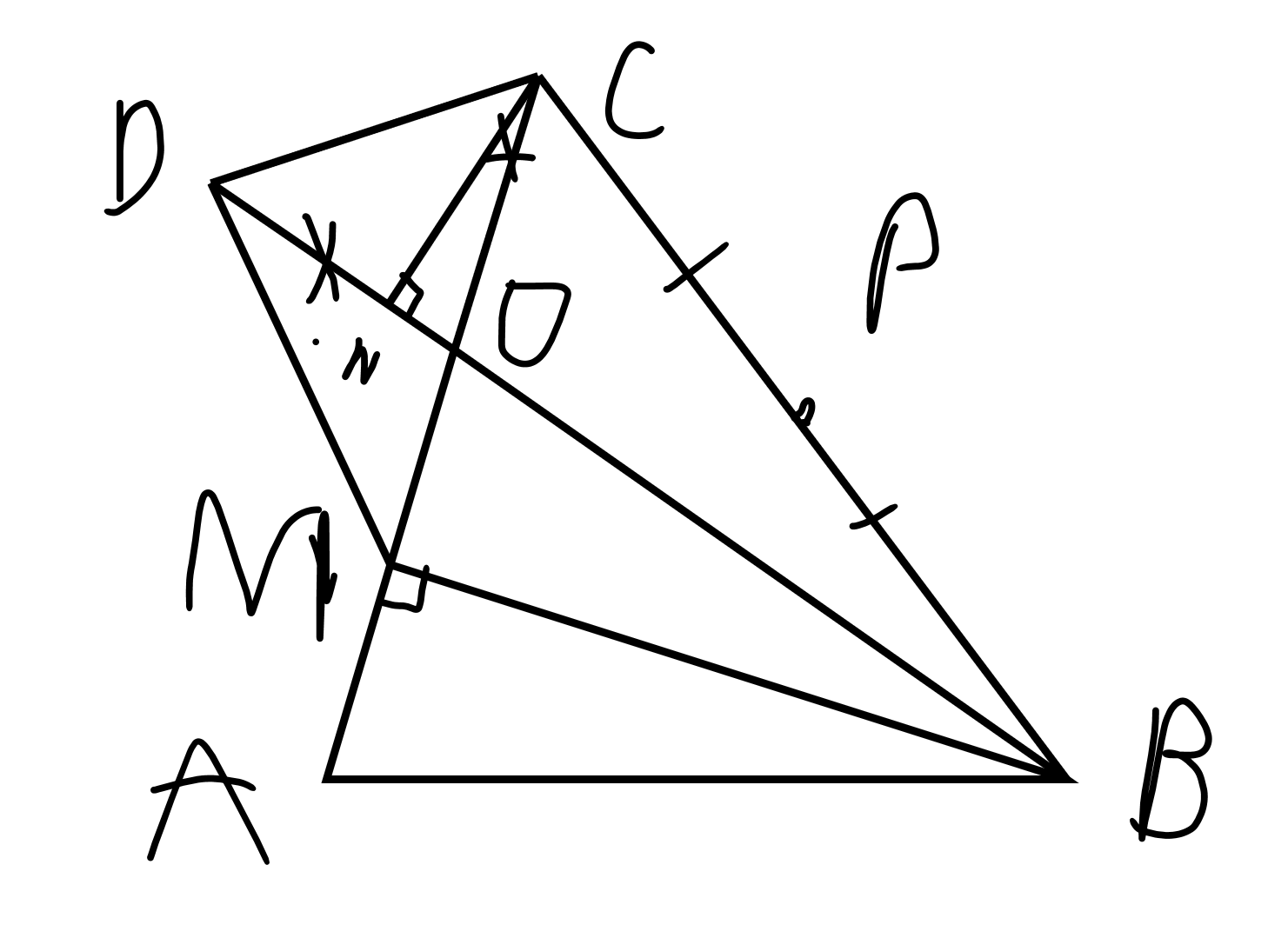
cho tam giác aob trên tia đối tia oa,ob lấy lần lượt c và d sao cho oc=od từ b kẻ bm vuông góc với ac, cn vuông góc với bd gọi p là tđ của bc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số có 3 chữ số đó là \(\overline{8ab}\)
Theo đề bài ta có:
\(\overline{8ab}=11\times\overline{ab}\)
\(800+\overline{ab}=11\times\overline{ab}\)
\(11\times\overline{ab}-\overline{ab}=800\)
\(10\times\overline{ab}=800\)
\(\overline{ab}=80\) hay \(\overline{8ab}=880\)
Vậy số cần tìm là 880

Giải:
Thời gian đi xe đạp của người đó là:
\(\dfrac{115}{12}\) : 23 = \(\dfrac{5}{12}\) (giờ)
\(\dfrac{5}{12}\) giờ = 25 phút
Đáp số 25 phút

Gọi số cam ban đầu trong rổ là \(x\) (quả) \(\left(x\inℕ^∗\right)\)
Theo đề bài ta có:
\(x-\left(\dfrac{3}{5}x+5\right)=9\)
\(\Rightarrow x-\dfrac{3}{5}x-5=9\)
\(\Rightarrow x-\dfrac{3}{5}x=9+5\)
\(\Rightarrow\dfrac{2}{5}x=14\)
\(\Rightarrow x=14:\dfrac{2}{5}\)
\(\Rightarrow x=35\) (thỏa mãn điều kiện)
Vậy...
9 quả còn lại cộng 5 quả = 14 quả sẽ bằng \(\dfrac{2}{5}\) số cam
Số cam ban đầu ở rổ: 14: \(\dfrac{2}{5}\) = 35 quả

\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\ \Rightarrow\dfrac{x+y}{xy}=\dfrac{1}{6}\\ \Rightarrow xy=6\left(x+y\right)\\ \Rightarrow xy-6x-6y=0\\ \Rightarrow x\left(y-6\right)-6\left(y-6\right)-36=0\\ \Rightarrow\left(y-6\right)\left(x-6\right)=36\)
Ta có bảng:
| y-6 | 36 | 1 | -1 | -36 | 2 | 18 | -2 | -18 | 3 | 12 | -3 | -12 | 4 | 9 | -9 | -4 | 6 | -6 | |||||
| x-6 | 1 | 36 | -36 | -1 | 18 | 2 | -18 | -2 | 12 | 3 | -12 | -3 | 9 | 4 | -4 | -9 | 6 | -6 | |||||
| y | 42 | 7 | 5 | -30 | 8 | 24 | 4 | -12 | 9 | 18 | 3 | -6 | 10 | 15 | -3 | 2 | 12 | 0 | |||||
| x | 7 | 42 | -30 | 5 | 24 | 8 | -12 | 4 | 18 | 9 | -6 | 3 | 15 | 10 | 2 | -3 | 12 | 0 |
Mà x,y nguyên dương nên (bạn tự chọn lại nhé)
`1/x + 1/y = 1/6`
`<=> (x+y)/(xy) = 1/6`
`<=> xy = 6x + 6y`
`<=> xy - 6x - 6y = 0`
`<=> x(y-6) - 6(y-6) = 36`
`<=> (x-6)(y-6) = 36`
Do `x-6, y-6 in ZZ` nên `(x-6) in Ư(36)`.
Đến đây bạn tự chia trường hợp và làm nhé.

\(1+2+3+...+x=55\)
=>\(x\cdot\dfrac{\left(x+1\right)}{2}=55\)
=>x(x+1)=110
=>\(x^2+x-110=0\)
=>(x+11)(x-10)=0
=>\(\left[{}\begin{matrix}x+11=0\\x-10=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-11\left(loại\right)\\x=10\left(nhận\right)\end{matrix}\right.\)
Vậy: x=10
\(1+2+3+...+x=55\)
\(\dfrac{x\left(x+1\right)}{2}=55\)
\(x\left(x+1\right)=2\cdot55=110\)
\(x^2+x-110=0\)
\(x^2-10x+11x-110=0\\ x\left(x-10\right)+11\left(x-10\right)=0\\ \left(x-10\right)\left(x+11\right)=0\\ \left[{}\begin{matrix}x=10\\x=-11\end{matrix}\right.\)

Bài 7:
p là số nguyên tố lớn hơn 3
=>p=3k+1 hoặc p=3k+2
Nếu p=3k+1 thì \(8p+1=8\left(3k+1\right)+1=24k+9=3\left(8k+3\right)⋮3\)
=>Loại
=>p=3k+2
\(4p+1=4\left(3k+2\right)+1=12k+9=3\left(4k+3\right)⋮3\)
=>4p+1 là hợp số
Bài 6:
a: TH1: p=3
p+2=3+2=5; p+4=3+4=7
=>Nhận
TH2: p=3k+1
p+2=3k+1+2=3k+3=3(k+1)
=>Loại
TH3: p=3k+2
p+4=3k+2+4=3k+6=3(k+2)
=>Loại
b: TH1: p=5
p+2=5+2=7; p+6=5+6=11; p+18=5+18=23; p+24=5+24=29
=>Nhận
TH2: p=5k+1
p+24=5k+1+24=5k+25=5(k+5)
=>Loại
TH3: p=5k+2
p+18=5k+2+18=5k+20=5(k+4)
=>Loại
TH4: p=5k+3
p+2=5k+3+2=5k+5=5(k+1)
=>Loại
TH5: p=5k+4
p+6=5k+4+6=5k+10=5(k+2)
=>Loại
Vậy: p=5
Bài 5:
Với p=2 => 7p+5=7*2 + 5 = 19 (tm)
Với p>3
TH1: p=3k+1
=> 7(3k+1)+5=21k+7+5=21k+12=3(7k+4) ⋮ 3
=> 7p+5 là hợp số
TH2: p=3k+2
=>7(3k+2)+5=21k+14+5=21k+19
Vì p là số nguyên tố lớn hơn 3 => p lẻ => 3k + 2 lẻ => 3k lẻ => k lẻ
k lẻ => 21k lẻ => 21k + 19 chẵn => 21k+19 ⋮ 2
=> 7p+5 là hơn số
Vậy có p=2 là thỏa mãn

