cho tam giác abc vuông tại a đường cao ah biết ab = 6cm ac = 8cm. tính bc.ah. tính bh, ch. đường phân giác góc abc cắt ac tại i. gọi k là giao điểm ah và bi. chứng minh góc aib=góc hkb và ai2= ic.kh
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA~ΔABC
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
ΔHBA~ΔABC
=>\(\dfrac{BA}{BC}=\dfrac{HB}{AB}\left(1\right)\)
ΔHBA~ΔABC
=>\(\dfrac{HA}{AC}=\dfrac{BA}{BC}\)
=>\(HA=\dfrac{3\cdot4}{5}=2,4\left(cm\right)\)
c: Xét ΔABC có BN là phân giác
nên \(\dfrac{BA}{BC}=\dfrac{NA}{NC}\left(2\right)\)
Xét ΔBHA có BM là phân giác
nên \(\dfrac{BH}{BA}=\dfrac{MH}{MA}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{NA}{NC}=\dfrac{MH}{MA}\)
=>\(MA\cdot NA=MH\cdot NC\)

x+y+z=1
=>\(\left\{{}\begin{matrix}x+y=1-z\\y+z=1-x\\x+z=1-y\end{matrix}\right.\)
\(P=\dfrac{\left(x+y\right)^2}{\left(xy+z\right)}\cdot\dfrac{\left(y+z\right)^2}{yz+x}\cdot\dfrac{\left(z+x\right)^2}{zx+y}\)
\(=\dfrac{\left(x+y\right)^2}{\left(xy+1-x-y\right)}\cdot\dfrac{\left(y+z\right)^2}{\left(yz+1-y-z\right)}\cdot\dfrac{\left(x+z\right)^2}{zx+1-x-z}\)
\(=\dfrac{\left(x+y\right)^2}{\left[x\left(y-1\right)-\left(y-1\right)\right]}\cdot\dfrac{\left(y+z\right)^2}{\left[y\left(z-1\right)-\left(z-1\right)\right]}\cdot\dfrac{\left(x+z\right)^2}{\left[z\left(x-1\right)-\left(x-1\right)\right]}\)
\(=\dfrac{\left(x+y\right)^2}{\left(y-1\right)\left(x-1\right)}\cdot\dfrac{\left(y+z\right)^2}{\left(z-1\right)\left(y-1\right)}\cdot\dfrac{\left(x+z\right)^2}{\left(x-1\right)\left(z-1\right)}\)
\(=\dfrac{\left(1-z\right)^2}{\left(z-1\right)^2}\cdot\dfrac{\left(1-x\right)^2}{\left(x-1\right)^2}\cdot\dfrac{\left(1-y\right)^2}{\left(y-1\right)^2}\)
=1

Xét ΔCAB vuông tại A và ΔCDE vuông tại D có
\(\widehat{ACB}=\widehat{DCE}\)(hai góc đối đỉnh)
Do đó: ΔCAB~ΔCDE
=>\(\dfrac{AC}{DC}=\dfrac{AB}{DE}\)
=>\(\dfrac{AB}{48}=\dfrac{120}{32}\)
=>\(AB=120\cdot\dfrac{48}{32}=120\cdot\dfrac{3}{2}=180\)(m)

d) \(\left(2024-x\right)^3+\left(2026-x\right)^3+\left(2x-4050\right)^3=0\) (1)
Đặt: \(\left\{{}\begin{matrix}2024-x=a\\2026-x=b\end{matrix}\right.\Rightarrow2x-4050=-\left(a+b\right)\) (*)
Thay (*) vào pt (1), ta được:
\(a^3+b^3+\left[-\left(a+b\right)\right]^3=0\)
\(\Leftrightarrow\left(a+b\right)^3-3ab\left(a+b\right)-\left(a+b\right)^3=0\)
\(\Leftrightarrow-3ab\left(a+b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=0\\b=0\\a+b=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2024-x=0\\2026-x=0\\2x-4050=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2024\\x=2026\\x=2025\end{matrix}\right.\)
Vậy \(S=\left\{2024;2025;2026\right\}\).

Câu 16:
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{ACB}\) chung
Do đó: ΔACB~ΔHCA
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=10^2-8^2=36=6^2\)
=>AC=6(cm)
ΔACB~ΔHCA
=>\(\dfrac{AC}{HC}=\dfrac{CB}{CA}\)
=>\(HC=\dfrac{AC^2}{BC}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
HB+HC=BC
=>HB+3,6=10
=>HB=6,4(cm)
Câu 17:
Gọi số tiền ban đầu MInh có là x(đồng)
(Điều kiện: x>0)
Số tiền ban đầu Na có là 320000-x(đồng)
Số tiền Minh có sau khi đưa cho Na 40 ngàn đồng là:
x-40000(đồng)
Số tiền Na có lúc sau là 320000-x+40000=360000-x(đồng)
Theo đề, ta có:
x-40000=360000-x
=>2x=400000
=>x=200000(nhận)
Vậy: Số tiền Minh có lúc đầu là 200 ngàn đồng
Số tiền Na có lúc đầu là 320-200=120 ngàn đồng

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)
ΔABC~ΔHBA
=>\(\dfrac{AC}{HA}=\dfrac{BC}{BA}\)
=>\(AH=\dfrac{9\cdot12}{15}=\dfrac{108}{15}=7,2\left(cm\right)\)
c: Xét ΔABC có AD là phân giác
nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)
=>\(\dfrac{DB}{9}=\dfrac{DC}{12}\)
=>\(\dfrac{DB}{3}=\dfrac{DC}{4}\)
mà DB+DC=BC=15cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{15}{7}\)
=>\(DB=\dfrac{45}{7}\left(cm\right);DC=\dfrac{60}{7}\left(cm\right)\)
Để giải bài toán này, chúng ta sẽ sử dụng các tính chất của tam giác vuông và tam giác đồng dạng.
a) Chứng minh tam giác ABC đồng dạng với tam giác HBA; AB^2=BC*HB
Trong tam giác vuông ���ABC, ta có:
- ��=9 cmAB=9cm
- ��=12 cmAC=12cm
Theo định lý Pythagoras, ta có ��=��2−��2=122−92=144−81=63BC=AC2−AB2=122−92=144−81=63.
Từ đó, ta có: ��2=92=81AB2=92=81 ��=63BC=63
Trong tam giác vuông ���ABC, đường cao ��AH là đường trung tuyến của tam giác vuông ���ABH, vì ��AH chia ��BC thành hai phần bằng nhau.
Vì vậy, ta có ��=��/2=63/2HB=BC/2=63/2.
Tam giác ���ABC và ���HBA có góc vuông tại �A và một góc nhọn khác là góc �B. Do đó, theo góc cạnh góc đồng dạng, chúng ta có thể kết luận ���ABC đồng dạng với ���HBA.
Vậy nên, ta có: ����=����/2=2����HBAB=BC/2AB=2BCAB ��2=��×��AB2=BC×HB
b) Tính độ dài cạnh BC và AH
- Độ dài cạnh ��BC: ��=63BC=63 (đã tính ở trên)
- Độ dài đoạn ��AH: ��AH chính là đoạn cao từ �A xuống ��BC, và trong tam giác vuông ���ABC, ��AH là cạnh huyền. Do đó, ��=��=12 cmAH=AC=12cm.
c) Tính độ dài các đoạn thẳng BD và CD
Tia phân giác của góc �A chia ��BC thành hai đoạn thẳng ��BD và ��CD sao cho: ����=����=912=34CDBD=ACAB=129=43
��BD và ��CD cũng chính là độ dài của các phân đoạn ��BC theo tỉ lệ 3:43:4.
Vậy: ��=33+4×��=37×63BD=3+43×BC=73×63 ��=43+4×��=47×63CD=3+44×BC=74×63
Vậy là chúng ta đã giải xong bài toán!

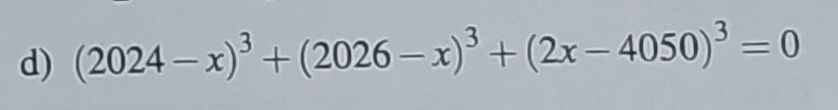
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA~ΔABC
=>\(\dfrac{HB}{AB}=\dfrac{BA}{BC}=\dfrac{HA}{AC}\)
=>\(\dfrac{HB}{6}=\dfrac{6}{10}=\dfrac{HA}{8}\)
=>\(HB=6\cdot\dfrac{6}{10}=3,6\left(cm\right);HA=6\cdot\dfrac{8}{10}=4,8\left(cm\right)\)
HB+HC=BC
=>HC+3,6=10
=>HC=6,4(cm)
Ta có: \(\widehat{AIB}+\widehat{ABI}=90^0\)(ΔABI vuông tại A)
\(\widehat{HKB}+\widehat{HBK}=90^0\)(ΔHBK vuông tại H)
mà \(\widehat{ABI}=\widehat{HBK}\)
nên \(\widehat{AIB}=\widehat{HKB}\)
=>\(\widehat{AIK}=\widehat{AKI}\)
=>ΔAIK cân tại A
Xét ΔBAH có BK là phân giác
nên \(\dfrac{BH}{BA}=\dfrac{HK}{KA}\left(1\right)\)
Xét ΔBAC có BI là phân giác
nên \(\dfrac{BA}{BC}=\dfrac{AI}{IC}\left(2\right)\)
ΔBHA~ΔBAC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{HK}{KA}=\dfrac{AI}{IC}\)
=>\(HK\cdot IC=AI^2\)