(-652)-{(-547)-352-[(-147)-(-735)+(2200+65)]}
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


⇔−4n+3⋮n+1⇔−4�+3⋮�+1
⇔−4n−4+7⋮n+1⇔−4�−4+7⋮�+1
⇔n+1∈{1;7}⇔�+1∈{1;7}
hay n∈{0;6}
⇔−4n+3⋮n+1⇔−4�+3⋮�+1
⇔−4n−4+7⋮n+1⇔−4�−4+7⋮�+1
⇔n+1∈{1;7}⇔�+1∈{1;7}
hay n∈{0;6}

\(S=\dfrac{2}{10.12}+\dfrac{2}{12.14}+\dfrac{2}{14.16}+...+\dfrac{2}{98.100}\)
\(S=\dfrac{1}{10}-\dfrac{1}{12}+\dfrac{1}{12}-\dfrac{1}{14}+\dfrac{1}{14}-\dfrac{1}{16}+...+\dfrac{1}{98}-\dfrac{1}{100}\)
\(S=\dfrac{1}{10}-\dfrac{1}{100}< \dfrac{1}{10}\) (đpcm)

a; \(\dfrac{-1}{8}\) + \(\dfrac{-5}{3}\)
= \(\dfrac{-3}{24}\) + \(\dfrac{-40}{24}\)
= \(\dfrac{-43}{24}\)
b; \(\dfrac{-5}{21}\) + \(\dfrac{-2}{21}\) + \(\dfrac{8}{24}\)
= -(\(\dfrac{5}{21}\) + \(\dfrac{2}{21}\)) + \(\dfrac{1}{3}\)
= - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\)
= 0
c; 0,25 + \(\dfrac{5}{6}\) - \(\dfrac{2}{3}\)
= \(\dfrac{1}{4}\) + \(\dfrac{5}{6}\) - \(\dfrac{2}{3}\)
= \(\dfrac{3}{12}\) + \(\dfrac{10}{12}\) - \(\dfrac{8}{12}\)
= \(\dfrac{5}{12}\)
d; \(\dfrac{2}{3}\) - \(\dfrac{5}{7}\).\(\dfrac{14}{25}\)
= \(\dfrac{2}{3}\) - \(\dfrac{2}{5}\)
= \(\dfrac{4}{15}\)
e; \(\dfrac{-2}{5}\).\(\dfrac{5}{8}\) + \(\dfrac{5}{8}\).\(\dfrac{3}{5}\)
= \(\dfrac{5}{8}\).(\(-\dfrac{2}{5}\) + \(\dfrac{3}{5}\))
= \(\dfrac{5}{8}\).\(\dfrac{1}{5}\)
= \(\dfrac{1}{8}\)
d; \(\dfrac{6}{7}\).\(\dfrac{8}{13}\) + \(\dfrac{6}{13}\).\(\dfrac{9}{7}\) - \(\dfrac{4}{13}\).\(\dfrac{6}{7}\)
= \(\dfrac{6}{7}\).(\(\dfrac{8}{13}\) + \(\dfrac{9}{13}\) - \(\dfrac{4}{13}\))
= \(\dfrac{6}{7}\).\(\dfrac{13}{13}\)
= \(\dfrac{6}{7}\)

Bạn nên viết lại đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.

Từ 25 đến 129 có số 30
Do đó chữ số tận cùng của tích là chữ số 0
\(25\rightarrow129\) có số \(30\)
Lấy \(0\) nhân với tận cùng của các số còn lại vẫn bằng \(0\)
Vậy tích các STN từ \(25\) đến \(129\) có chữ số tận cùng là \(0\)

\(7⋮\left(x+1\right)\Rightarrow\left(x+1\right)\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\\ Có:x+1=-7\Rightarrow x=-8\\ x+1=-1\Rightarrow x=-2\\ x+1=1\Rightarrow x=0\\ x+1=7\Rightarrow x=6\\ Vậy:x\in\left\{-8;-2;0;6\right\}\)
Ta có:
\(7⋮\left(x+1\right)\Rightarrow x+1\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)
Ta có bảng sau:
| \(x+1\) | \(1\) | \(-1\) | \(7\) | \(-7\) |
| \(x\) | \(0\) | \(-2\) | \(6\) | \(-8\) |
Vậy \(x\in\left\{0;-2;6;-8\right\}\)

Câu 1:
a; \(\dfrac{-9}{4}\) < 0; \(\dfrac{1}{3}\) > o
\(\dfrac{-9}{4}\) < \(\dfrac{1}{3}\)
b; \(\dfrac{-8}{3}\) < - 1
\(\dfrac{4}{-7}\) > - 1
Vậy \(\dfrac{-8}{3}\) < \(\dfrac{4}{-7}\)
c; \(\dfrac{9}{-5}\) < - 1
\(\dfrac{7}{-10}\) > - 1
Vậy \(\dfrac{9}{-5}\) < \(\dfrac{7}{-10}\)
Câu 2:
a; Viết các phân số theo thứ tự tăng dần
\(\dfrac{-1}{2}\); \(\dfrac{2}{7}\); \(\dfrac{2}{5}\)
b; \(\dfrac{-11}{4}\); \(\dfrac{-7}{3}\); \(\dfrac{12}{5}\)

Cứ 1 tia chung gốc sẽ tạo với 2021 - 1 tia còn lại số góc là: 2021 - 1 (góc)
Với 2021 tia chung gốc tạo được số góc là: (2021 - 1) x 2021 (góc)
Theo cách tính trên mỗi góc được tính hai lần nên số góc thực tế được tạo từ 2021 tia trong đó không có bất cứ hai tia nào đối nhau là:
(2021 - 1) x 2021: 2 = 2041210 (góc)
Kết luận:..
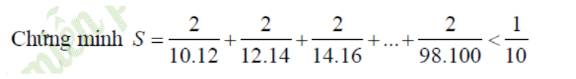

(-652) - {(-547) - 352 - [ (-147) - (-735) + (2200 + 65)]}
= (-652) + 547 + 352 - 147 - 735 - 2200 - 65
= - (652 - 352) + (547 - 147) - (735 + 65) - 2200
= - 300 + 400 - 1000 - 2200
= 100 - (1000 + 2200)
= 100 - 3200
= 3100
(-652) - {(-547) - 352 - [(-147) - (-735) + (2200 + 65)]}
= (-652) - {(-547) - 352 - [(-147) + 735 + 2265]}
= (-652) - {(-547) - 352 - [588 + 2265]}
= (-652) - {(-547) - 352 - 2853}
= (-652) - {(-899) - 2853}
= (-652) - (-3752)
= (-652) + 3752
= 3100