Bài 1. Thu gọn các biểu thức sau:
a) (x + 3)^3 + (x^2 + 1)(x – 2)
b) (2x – 1)^2 – (2 – x)^3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trả lời:
a, \(x^3-3x^2+3x-1=8\)
\(\Leftrightarrow\left(x-1\right)^3=2^3\)
\(\Rightarrow x-1=2\)
\(\Leftrightarrow x=3\)
Vậy x = 3 là nghiệm của pt.
a) \(x^3-3x^2+3x-1=8\)
\(\left(x-1\right)^3=2^3\)
\(x-1=2\)
\(\Leftrightarrow x=3\)
Vậy x = 3

ta có
\(ab^3-a^3b=ab\left(b^2-a^2\right)=ab\left(b-a\right)\left(b+a\right)\)

Trả lời:
b, \(-x\left(x-2\right)+4=\left(x+1\right)\left(1-x\right)\)
\(\Leftrightarrow-x^2+2x+4=1-x^2\)
\(\Leftrightarrow-x^2+2x+4-1+x^2=0\)
\(\Leftrightarrow2x+3=0\)
\(\Leftrightarrow2x=-3\)
\(\Leftrightarrow x=-\frac{3}{2}\)
Vậy x = - 3/2 là nghiệm của pt.
c, \(16x^2-\left(x-1\right)^2=0\)
\(\Leftrightarrow\left(4x-x+1\right)\left(4x+x-1\right)=0\)
\(\Leftrightarrow\left(3x+1\right)\left(5x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}3x+1=0\\5x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{3}\\x=\frac{1}{5}\end{cases}}}\)
Vậy x = - 1/3; x = 1/5 là nghiệm của pt.

6x2(x-y)-3x(y-x) = 6x^2 (x-y)- 3x (y-x) = -3x (2x+1) (y-x)
ờ xình xloi nhưng mình chép sai đề bài r ạ đẻ mình sửa lai là
6x2(x-y)2-3x(y-x)
mình cảm ơn ạ


b. ta có \(-x\left(x-2\right)+4=\left(x+1\right)\left(1-x\right)\Leftrightarrow-x^2+2x+4=1-x^2\)
\(\Leftrightarrow2x=-3\Leftrightarrow x=-\frac{3}{2}\)
c.\(16x^2=\left(x-1\right)^2\Leftrightarrow\orbr{\begin{cases}4x=x-1\\4x=1-x\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{3}\\x=\frac{1}{5}\end{cases}}}\)

Ta có: OA = OC (gt)
⇒ Δ∆OAC cân tại O
⇒∠A1∠A1= (18001800 - ∠∠(AOC) ) / 2 (tính chất tam giác cân) (1)
OB = OD (gt)
⇒ Δ∆OBD cân tại O
⇒ ∠B1∠B1= (18001800 - ∠∠(BOD) )/2 (tính chất tam giác cân) (2)
∠∠(AOC) = ∠∠(BOD) (đối đỉnh) (3)
Từ (1), (2), (3) suy ra: ∠A1∠A1 = ∠B1∠B1
⇒ AC // BD (vì có cặp góc ở vị tri so le trong bằng nhau)
Suy ra: Tứ giác ACBD là hình thang
Ta có: AB = OA + OB
CD = OC + OD
Mà OA = OC, OB = OD
Suy ra: AB = CD
Vậy hình thang ABCD là hình thang cân.
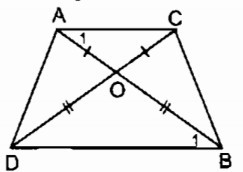
Ta có: OA = OC (gt)
⇒ ∆ OAC cân tại O
⇒ˆA1=(–ˆAOC)/2 (tính chất tam giác cân) (1)
OB = OD (gt)
⇒ ∆ OBD cân tại O
⇒ˆB1=(–ˆBOD)/2 (tính chất tam giác cân) (2)
ˆAOC=ˆBOD (đối đỉnh) (3)
Từ (1), (2) và (3) suy ra: ˆA1=ˆB1
⇒ AC // BD (vì có cặp góc ở vị trí so le trong bằng nhau)
Suy ra: Tứ giác ACBD là hình thang
Ta có: AB = OA + OB
CD = OC + OD
Mà OA = OC, OB = OD
Suy ra: AB = CD
Vậy hình thang ACBD là hình thang cân.
a.ta có
\(\left(x+3\right)^3+\left(x^2+1\right)\left(x-2\right)=x^3+9x^2+27x+27+x^3-2x^2+x-2\)
\(=2x^3+7x^2+28x+25\)
b.\(\left(2x-1\right)^2-\left(2-x\right)^3=4x^2-4x+1+x^3-6x^2+12x-8\)
\(=x^3-2x^2+8x-7\)
a) (x + 3)3 + (x2 + 1)(x - 2)
= x3 + 9x2 + 27x + 27 + x3 - 2x + x - 2
= x3 + x3 + 9x2 + 27x - 2x + x + 27 - 2
= 2x3 + 9x2 + 26x + 25
b) (2x - 1)2 - (2 - x)3
= 4x2 - 4x + 1 - ( 8 - 12x + 6x2 - x3)
= 4x2 - 4x + 1 - 8 + 12x - 6x2 + x3
= x3 + 4x2 - 6x2 + 12x - 4x + 1 - 8
= x3 - 2x2 + 8x - 7