cho các số 1,2,3,4,5,....,99,100. Xếp tùy ý tất cả 100 số trên nối tiếp nhau thành dãy ta được số P. CM số P không chia hết cho 2016.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(ĐK:x\inℝ\)
\(\sqrt[3]{2x+3}+1=x^3+3x^2+2x\Leftrightarrow\sqrt[3]{2x+3}=x^3+3x^2+2x-1\)\(\Leftrightarrow2x+3=\left(x^3+3x^2+2x-1\right)^3\)\(\Leftrightarrow\left(x+2\right)\left(x^2+x-1\right)\left(x^6+6x^5+14x^4+14x^3+4x^2-x+2\right)=0\)
Dễ dàng kiểm tra \(x^6+6x^5+14x^4+14x^3+4x^2-x+2\)không thể phân tích thành nhân tử với các hệ số nguyên nên không có nghiệm nguyên và hữu tỉ
\(\Rightarrow x\in\left\{-2;\frac{\sqrt{5}-1}{2};\frac{-1-\sqrt{5}}{2}\right\}\)
Thử lại ta thấy ba giá trị trên đều thỏa mãn phương trình
Vậy tập nghiệm của phương trình \(S=\left\{\frac{\pm\sqrt{5}-1}{2};-2\right\}\)


a) Phương trình \(x^2-2mx-2m-1=0\)có các hệ số a = 1; b = - 2m; c = - 2m - 1
\(\Delta=\left(-2m\right)^2-4\left(-2m-1\right)=4m^2+8m+4=4\left(m+1\right)^2\ge0\forall m\)
Vậy phương trình luôn có 2 nghiệm x1, x2 với mọi m (đpcm)
b) Theo Viète, ta có: \(x_1+x_2=2m;x_1x_2=-2m-1\)
Hệ thức \(\frac{x_1}{x_2}+\frac{x_2}{x_1}=\frac{-5}{2}\Leftrightarrow2\left(x_1^2+x_2^2\right)=-5x_1x_2\)
\(\Leftrightarrow2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]=-5x_1x_2\)hay \(2\left(4m^2+4m+2\right)=10m+5\Leftrightarrow8m^2-2m-1=0\)\(\Leftrightarrow\orbr{\begin{cases}m=\frac{1}{2}\\m=-\frac{1}{4}\end{cases}}\)
Vậy \(m=\frac{1}{2}\)hoặc \(m=-\frac{1}{4}\)thì phương trình có 2 nghiệm x1, x2 thỏa mãn\(\frac{x_1}{x_2}+\frac{x_2}{x_1}=\frac{-5}{2}\)


\(P=\frac{1}{\sqrt{a+3}}+\frac{1}{\sqrt{b+3}}\ge\frac{\left(1+1\right)^2}{\sqrt{a+3}+\sqrt{b+3}}=\frac{4}{\sqrt{a+3}+\sqrt{b+3}}\)
Ta có:
\(\left(\sqrt{a+3}.1+\sqrt{b+3}.1\right)^2\le\left(1^2+1^2\right)\left(a+3+b+3\right)\le16\)
\(\Rightarrow\sqrt{a+3}+\sqrt{b+3}\le\sqrt{16}=4\)
\(\Rightarrow P\ge\frac{4}{\sqrt{a+3}+\sqrt{b+3}}\ge\frac{4}{4}=1\).
Dấu \(=\)xảy ra khi \(a=b=1\).
\(P=\frac{1}{\sqrt{a+3}}+\frac{1}{\sqrt{b+3}}\Rightarrow P^2=\left(\frac{1}{a+3}+\frac{1}{b+3}\right)+\frac{2}{\sqrt{\left(a+3\right)\left(b+3\right)}}\)\(\ge\frac{4}{\left(a+b\right)+6}+\frac{2}{\frac{\left(a+3\right)+\left(b+3\right)}{2}}=\frac{8}{a+b+6}\ge\frac{8}{2+6}=1\)
\(\Rightarrow P\ge1\)
Đẳng thức xảy ra khi a = b = 1

Ta có A = 5x2 - 2xy + 2y2 - 4x + 2y + 3
=> 2A = 10x2 - 4xy + 4y2 - 8x + 4y + 6
= (x2 - 4xy + 4y2) - 2(x - 2y) + 1 + 9x2 - 6x + 1 + 4
= \(\left(x-2y\right)^2-2\left(x-2y\right)+1+9\left(x^2-\frac{2}{3}x+\frac{1}{9}\right)+4\)
\(=\left(x-2y-1\right)^2+9\left(x-\frac{1}{3}\right)^2+4\)\(\ge4\)
=> A \(\ge\)2
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x-2y-=0\\x-\frac{1}{3}=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x-2y=1\\x=\frac{1}{3}\end{cases}}\Leftrightarrow\hept{\begin{cases}y=-\frac{1}{3}\\x=\frac{1}{3}\end{cases}}\)
Vậy khi x = 1/3 ; y = -1/3 thì A đạt GTNN
\(A=5x^2+2y^2-2xy-4x+2y\)\(+3\)
\(=\left(x^2-2xy+y^2\right)+\)\(\left(4x^2-4x+1\right)+\)\(\left(y^2+2y+1\right)+1\)
\(Tacó\)

\(\hept{\begin{cases}x^2+9y^2=10\\x+3y+8=12xy\end{cases}}\Leftrightarrow\hept{\begin{cases}x^2+6xy+9y^2=10+6xy\\x+3y=12xy-8\end{cases}}\Rightarrow\hept{\begin{cases}\left(x+3y\right)^2=10+6xy\\\left(x+3y\right)^2=\left(12xy-8\right)^2\end{cases}}\)
\(\Rightarrow10+6xy=\left(12xy-8\right)^2\)
\(\Leftrightarrow144x^2y^2-198xy+54=0\)
\(\Leftrightarrow\orbr{\begin{cases}xy=1\\xy=\frac{3}{8}\end{cases}}\)
- Với \(xy=1\):
\(\hept{\begin{cases}xy=1\\x+3y+8=12\end{cases}}\Leftrightarrow\hept{\begin{cases}y=\frac{1}{x}\\x+\frac{3}{x}-4=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3,y=\frac{1}{3}\\x=1,y=1\end{cases}}\)
- Với \(xy=\frac{3}{8}\):
\(\hept{\begin{cases}xy=\frac{3}{8}\\x+3y+8=4\end{cases}}\Leftrightarrow\hept{\begin{cases}y=\frac{3}{8x}\\x+\frac{9}{8x}+4=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{-7-\sqrt{31}}{4},y=\frac{-7+\sqrt{31}}{12}\\x=\frac{-7+\sqrt{31}}{4},y=\frac{-7-\sqrt{31}}{12}\end{cases}}\)
Thử lại ta đều thấy thỏa mãn.
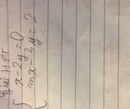
Đáp án là 720 .
Nếu số P \(⋮\)2016 thì số P \(⋮\)3 vì 2016 \(⋮\)3.
Tổng các chữ số của P là 5050 \(⋮̸\)3 .
\(\Rightarrow\)(đpcm)