Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với \(n>2\) ta có: \(\dfrac{n+\left(n+1\right)}{n^2.\left(n+1\right)^2}=\dfrac{1}{n\left(n+1\right)}\left[\dfrac{n}{n\left(n+1\right)}+\dfrac{n+1}{n\left(n+1\right)}\right]=\dfrac{1}{n\left(n+1\right)}\left(\dfrac{1}{n}+\dfrac{1}{n+1}\right)< \dfrac{1}{n\left(n+1\right)}\)
\(\Rightarrow A< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{9.10}\)
\(\Rightarrow A< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
\(\Rightarrow A< 1-\dfrac{1}{10}< 1\) (đpcm)

đáp án đây
Trải qua hơn 250 năm, các nhà toán học vẫn chưa chứng minh được giả thuyết này và chúng được mọi người gọi là giả thuyết Christian Goldbach tam nguyên.
Theo Toán học hiện đại, Terence Tao (học tại trường đại học California, Mỹ) là người tiếp cận gần nhất với bài toán của Christian Goldbach. Ông đã nghiên cứu và chứng minh rằng mỗi số lẻ là tổng của tối đa 5 số nguyên tố. Và hy vọng có thể giảm từ 5 xuống còn 3 như giả thuyết mà Christian Goldbach đã đưa ra.

\(x>-\dfrac{39}{13}\)
\(\Rightarrow x>-3\)
Mà x là số nguyên và là số nguyên nhỏ nhất thỏa mãn
\(\Rightarrow\text{x}\text{ }=-2\)


a; P = \(\dfrac{-9}{n+1}\) (đk n ≠ -1)
P \(\in\) Z ⇔ - 9 ⋮ n + 1
⇒ n + 1 \(\in\) Ư(-9) = {-9; -3; -1; 1; 3; 9}
Lập bảng ta có:
| n + 1 | -9 | -3 | -1 | 1 | 3 | 9 |
| n | -10 | -4 | -2 | 0 | 2 | 8 |
Theo bảng trên ta có:
n \(\in\) {-10; -4; -2; 0; 2; 8}
Kết luận: P = \(\dfrac{-9}{n+1}\) nguyên khi n \(\in\) {-10; -4; -2; 0; 2; 8}

A = \(\dfrac{2}{2.3}\) + \(\dfrac{2}{3.4}\) + \(\dfrac{2}{4.5}\) + ... + \(\dfrac{2}{199.200}\)
A = 2. (\(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\) + \(\dfrac{1}{4.5}\) + ... + \(\dfrac{1}{199.200}\))
A = 2.(\(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) + ... + \(\dfrac{1}{199}\) - \(\dfrac{1}{200}\))
A = 2.(\(\dfrac{1}{2}\) - \(\dfrac{1}{200}\))
A = 2. \(\dfrac{99}{200}\)
A = \(\dfrac{99}{100}\)

Lời giải:
Gọi tổng trên là $A$
$A=2(\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{199.200})$
$=2(\frac{3-2}{2.3}+\frac{4-3}{3.4}+\frac{5-4}{4.5}+...+\frac{200-199}{199.200})$
$=2(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+....+\frac{1}{199}-\frac{1}{200})$
$=2(\frac{1}{2}-\frac{1}{200})=1-\frac{1}{100}=\frac{99}{100}$

A = {\(x\) \(\in\) Z/\(x\) ⋮ 3; -12 ≤ \(x\) < 120}
Ta có: \(x\) \(⋮\) 3
⇒ \(x\) \(\in\) B(3) = {...-15; -12; -9; -6; - 3; 0; 3; 6; 9; 12...;117; 120;...}
Vì -12 ≤ \(x\) < 120
⇒ \(x\) \(\in\) {-12;-9; -6; -3; 0; 3; 6; 9; 12;...; 117}
Tình tổng các phần tử có trong tập A
A = -12 + (-9) + (-6) + (-3) + .....+ 117
Xét dãy số -12; -9; -6; -3; 0; 3;..; 117
Dãy số trên là dãy số cách đều với khoảng cách là: 3 - 0 = 3
Dãy số trên có số số hạng là: [117 - (-12) ] : 3 + 1 = 44
Tổng của tất cả các phần tử có trong tập A là
A = [117 + (-12)] x 44 : 2 = 2310
Kết luận: A = {-12; -9; -6; -3; 0; 3; 6; 9;...;117}
A có 44 phần tử
Tổng các phần tử có trong A là 2310
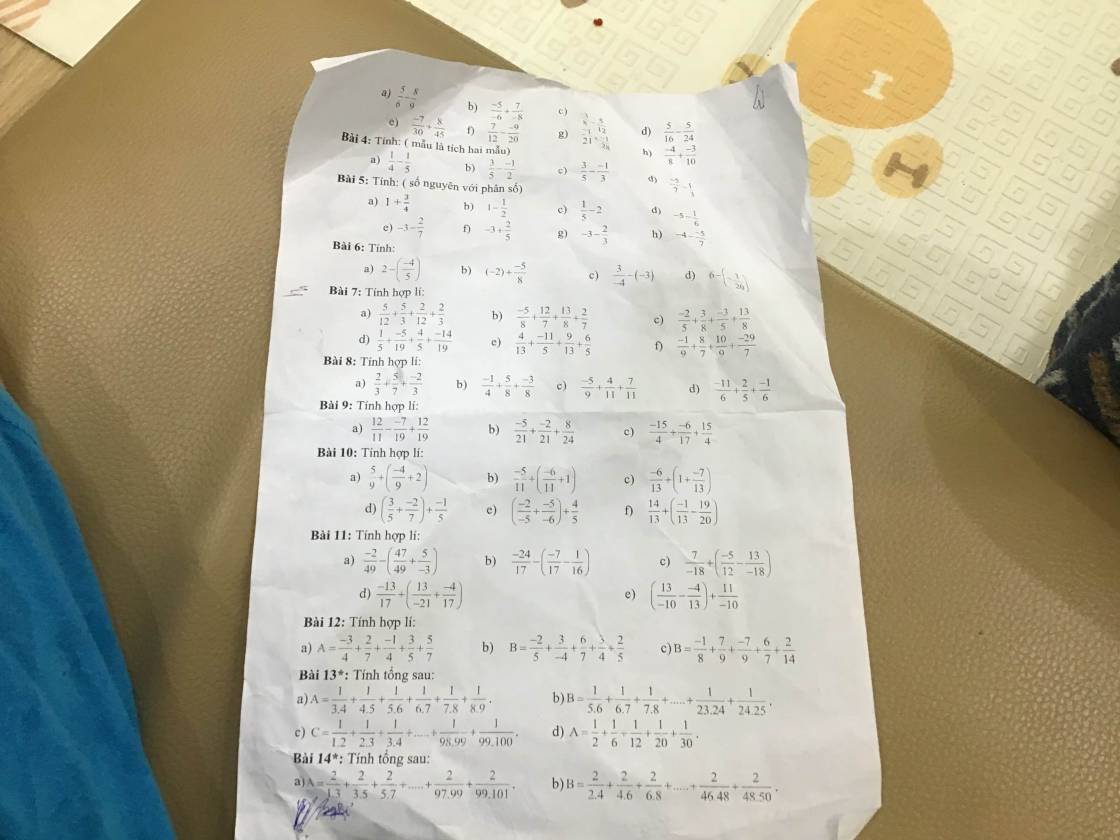
Có quá nhiều bài, thứ nhất em đăng tách ra, thứ hai chụp gần cận cho rõ, thứ ba em chỉ đăng bài cần giúp