Một cái bục hình lăng trụ đứng có kích thước như Hình 12.
a) Người ta muốn sơn tất cả các mặt của cái bục trừ mặt tiếp xúc với mặt đất. Diện tích cần phải sơn là bao nhiêu?
b) Tính thể tích của cái bục.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c: \(P=A:B=\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}:\dfrac{\sqrt{x}-1}{\sqrt{x}+3}\)
\(=\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{\sqrt{x}-1}=\dfrac{2\sqrt{x}+3}{\sqrt{x}-1}\)
Để P là số nguyên thì \(2\sqrt{x}+3⋮\sqrt{x}-1\)
=>\(2\sqrt{x}-2+5⋮\sqrt{x}-1\)
=>\(5⋮\sqrt{x}-1\)
=>\(\sqrt{x}-1\in\left\{1;-1;5;-5\right\}\)
=>\(\sqrt{x}\in\left\{2;0;6;-4\right\}\)
=>\(\sqrt{x}\in\left\{2;0;6\right\}\)
=>\(x\in\left\{4;0;36\right\}\)
mà x lớn nhất
nên x=36

Cửa hàng đã bán được:
\(\dfrac{3}{8}+\dfrac{2}{7}=\dfrac{21}{56}+\dfrac{16}{56}=\dfrac{37}{56}\)(tổng số gạo)

Số học sinh khá chiếm:
\(\dfrac{1}{5}:\dfrac{3}{7}=\dfrac{1}{5}\times\dfrac{7}{3}=\dfrac{7}{15}\)(tổng số học sinh)
Số học sinh trung bình chiếm:
\(1-\dfrac{1}{5}-\dfrac{7}{15}=\dfrac{4}{5}-\dfrac{7}{15}=\dfrac{5}{15}=\dfrac{1}{3}\)(tổng số học sinh)
Tổng số học sinh là \(45:\dfrac{1}{3}=135\left(bạn\right)\)
Số học sinh giỏi là \(135\cdot\dfrac{1}{5}=27\left(bạn\right)\)
Số học sinh khá là:
135-45-27=63(bạn)

a: ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\)
=>\(\widehat{ACB}=50^0\)
ΔABC cân tại A
=>\(\widehat{BAC}=180^0-2\cdot\widehat{ABC}=180^0-2\cdot50^0=80^0\)
b: Xét ΔNBC vuông tại N và ΔMCB vuông tại M có
BC chung
\(\widehat{NBC}=\widehat{MCB}\)(ΔABC cân tại A)
Do đó: ΔNBC=ΔMCB
=>CN=MB
c: ΔNBC=ΔMCB
=>\(\widehat{NCB}=\widehat{MBC}\)
=>\(\widehat{HBC}=\widehat{HCB}\)
=>ΔHBC cân tại H
Xét ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
Do đó: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
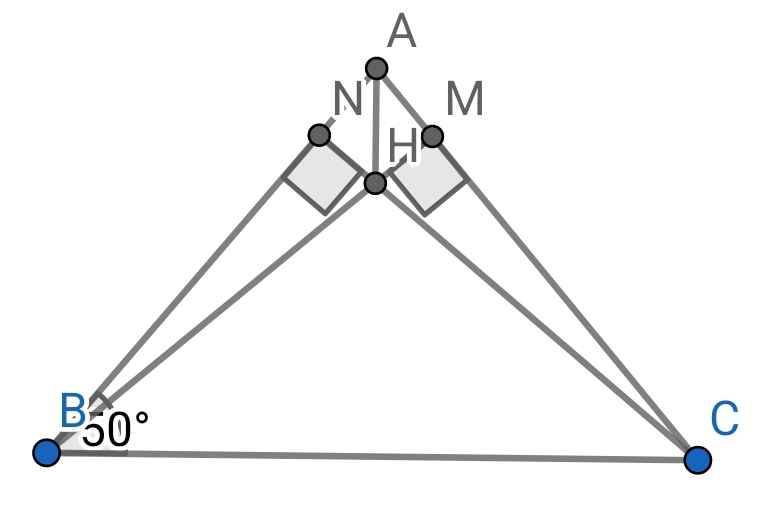
a) ∆ABC cân tại A (gt)
⇒ ∠ABC = ∠ACB = 50⁰
∠ABC + ∠ACB + ∠BAC = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠BAC = 180⁰ - (∠ABC + ∠ACB)
= 180⁰ - (50⁰ + 50⁰)
= 80⁰
b) Ta có:
∠ABC = ∠ACB (cmt)
⇒ ∠NBC = ∠MCB
Xét hai tam giác vuông: ∆NBC và ∆MCB có:
BC là cạnh chung
∠NBC = ∠MCB (cmt)
⇒ ∆NBC = ∆MCB (cạnh huyền - góc nhọn)
⇒ CN = BM (hai cạnh tương ứng)
Hay BM = CN
c) ∆ABC cân tại A (gt)
BM là đường cao (gt)
CN là đường cao thứ hai (gt)
⇒ AH là đường cao thứ ba
⇒ AH cũng là đường phân giác
⇒ AH là tia phân giác của ∠BAC

\(\dfrac{15}{6}=2,5;\dfrac{12}{12}=1;\dfrac{9}{8}=1,125;\dfrac{10}{8}=1,25\)
mà 2,5>1,25>1,125>1
nên \(\dfrac{15}{6}>\dfrac{10}{8}>\dfrac{9}{8}>\dfrac{12}{12}\)
\(\dfrac{12}{12}\) = 1 < \(\dfrac{9}{8}\) < \(\dfrac{10}{8}\) < \(\dfrac{20}{8}\) = \(\dfrac{15}{6}\)
Vậy các phân số đã cho được sắp xếp theo thứ tự từ lớn đến bé là:
\(\dfrac{15}{6}\); \(\dfrac{10}{8}\); \(\dfrac{9}{8}\); \(\dfrac{12}{12}\)

a: Độ dài đáy lớn là:
40x1,5=60(m)
Chiều cao là \(\left(40+60\right)\times\dfrac{1}{2}=50\left(m\right)\)
Diện tích mảnh vườn là \(\left(40+60\right)\times\dfrac{50}{2}=50\times50=2500\left(m^2\right)\)
b: Diện tích đất trồng hoa chiếm:
100%-50%-30%=20%(tổng diện tích)
Diện tích đất trồng hoa là:
2500x20%=500(m2)

459:3+459:9
\(=459\times\dfrac{1}{3}+459\times\dfrac{1}{9}\)
\(=459\times\left(\dfrac{1}{3}+\dfrac{1}{9}\right)=459\times\dfrac{4}{9}=204\)
459 : 3 + 459 : 9
= 459 x (\(\dfrac{1}{3}\) + \(\dfrac{1}{9}\))
= 459 x \(\dfrac{4}{9}\)
= 204