Cùng một lúc, có một ca nô ngược dòng từ A đến B và một ca nô xuôi dòng từ B đến A. Hai ca nô gặp nhau tại điểm C cách B một quãng đường bằng 3/5 quãng đường AB. Hỏi một chiếc phao trôi trong 1/4 giờ được một quãng đường dài bao nhiêu mét. Biết rằngvận tốc khi nước yên lặng của hai ca nô bằng nhau và ca nô đi từ B đến A có vận tốc 12km/giờ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 4 2024
Pt hoành độ giao điểm: \(x^2=2x-m+3\) (1)
\(\Leftrightarrow x^2-2x+m-3=0\)
\(\Delta'=1-\left(m-3\right)>0\Rightarrow m< 4\)
Theo định lý Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m-3\end{matrix}\right.\)
Do \(x_1\) là nghiệm của (1) nên: \(x_1^2=2x_1-m+3\)
Thế vào:
\(x_1^2+12=2x_2-x_1x_2\)
\(\Leftrightarrow2x_1-m+3+12=2x_1-\left(m-3\right)\)
\(\Leftrightarrow x_1-x_2=6\)
\(\Rightarrow x_2=x_1-6\)
Thế vào \(x_1+x_2=2\Rightarrow x_1+x_1-6=2\)
\(\Rightarrow x_1=4\Rightarrow x_2=-2\)
Thay vào \(x_1x_2=m-3\Rightarrow m-3=-8\)
\(\Rightarrow m=-5\) (thỏa mãn)
1 tháng 5 2024
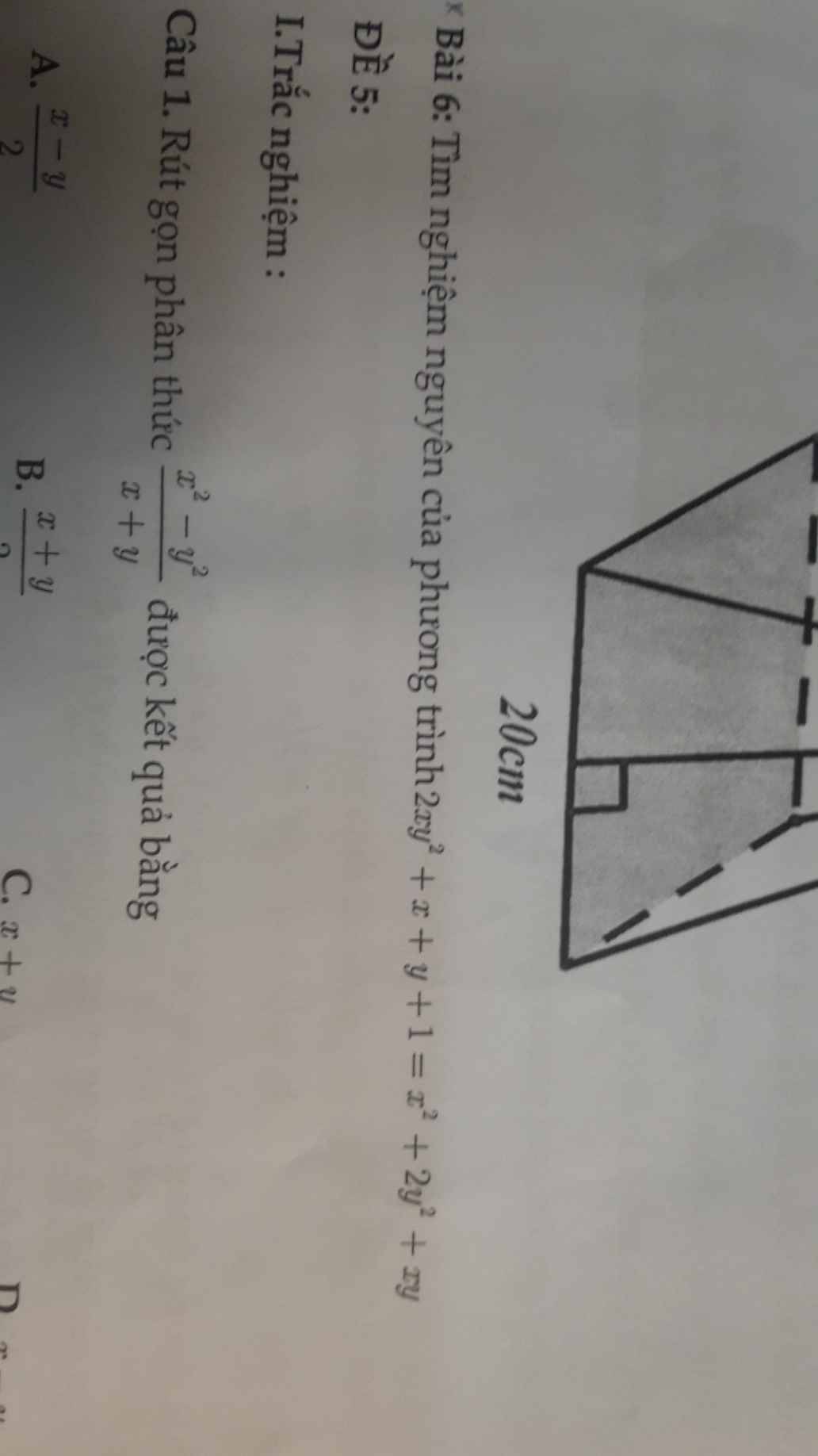
Bổ sung đề: ΔABC vuông tại A
a: Xét ΔEAB và ΔEND có
EA=EN
\(\widehat{AEB}=\widehat{NED}\)(hai góc đối đỉnh)
EB=ED
Do đó: ΔEAB=ΔEND
=>\(\widehat{EAB}=\widehat{END}\)
=>AB//ND
b: Ta có: AB//ND
AB\(\perp\)AC
Do đó: ND\(\perp\)AC
Ta có: ΔABC vuông tại A
mà AD là đường trung tuyến
nên \(AD=\dfrac{BC}{2}=AB=BD\)
=>ΔABD đều
Ta có: ΔABD đều
mà AE là đường trung tuyến
nên AE\(\perp\)BD
Xét ΔANC có
CE,ND là các đường cao
CE cắt ND tại D
Do đó: D là trực tâm của ΔANC
=>AD\(\perp\)NC
1 tháng 5 2024
a:
Sửa đề: Chiều dài là 25m; chiều rộng là 20m
Diện tích thửa ruộng là 25x20=500(m2)
b: Khối lượng thóc thu được là:
500:100x65=5x65=325(kg)
1 tháng 5 2024
\(\dfrac{-15}{8}\cdot\left(\dfrac{8}{-15}+\dfrac{32}{27}\right)\cdot\dfrac{15}{-7}\)
\(=\left(\dfrac{-15}{8}\cdot\dfrac{8}{-15}-\dfrac{15}{8}\cdot\dfrac{32}{27}\right)\cdot\dfrac{15}{-7}\)
\(=\left(1-4\cdot\dfrac{5}{9}\right)\cdot\dfrac{15}{-7}\)
\(=\dfrac{-11}{9}\cdot\dfrac{15}{-7}=\dfrac{165}{63}=\dfrac{55}{21}\)
LB
1
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 4 2024
\(\Leftrightarrow\left(x^2+xy\right)-\left(x+y\right)-\left(2xy^2-2y^2\right)=1\)
\(\Leftrightarrow x\left(x+y\right)-\left(x+y\right)-2y^2\left(x-1\right)=1\)
\(\Leftrightarrow\left(x-1\right)\left(x+y\right)-2y^2\left(x-1\right)=1\)
\(\Leftrightarrow\left(x-1\right)\left(x+y-2y^2\right)=1=1.1=\left(-1\right).\left(-1\right)\)
Th1: \(\left\{{}\begin{matrix}x-1=1\\x+y-2y^2=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\2+y-2y^2=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\2y^2-y-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\\left[{}\begin{matrix}y=1\\y=-\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\end{matrix}\right.\)
Th2: \(\left\{{}\begin{matrix}x-1=-1\\x+y-2y^2=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0\\0+y-2y^2=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\2y^2-y-1=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0\\\left[{}\begin{matrix}y=1\\y=-\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy pt có 2 cặp nghiệm nguyên \(\left(x;y\right)=\left(2;1\right);\left(0;1\right)\)
1 tháng 5 2024
Thời gian kể từ khi hai xe xuất phát đến lúc gặp nhau là:
8h-7h15p=45p=0,75(giờ)
Tổng vận tốc hai xe là 50+40=90(km/h)
Độ dài quãng đường từ bến A đến bến B là:
90x0,75=67,5(km)