Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
e; \(\dfrac{10}{21}\) - \(\dfrac{3}{8}\) : \(\dfrac{15}{4}\)
= \(\dfrac{10}{21}\) - \(\dfrac{3}{8}\) x \(\dfrac{4}{15}\)
= \(\dfrac{10}{21}\) - \(\dfrac{1}{10}\)
= \(\dfrac{100}{210}\) - \(\dfrac{21}{210}\)
= \(\dfrac{79}{210}\)
f; (\(\dfrac{2}{3}\) + \(\dfrac{3}{4}\)).(\(\dfrac{5}{7}\) + \(\dfrac{5}{14}\))
= (\(\dfrac{8}{12}\) + \(\dfrac{9}{12}\)).(\(\dfrac{10}{14}\) + \(\dfrac{5}{14}\))
= \(\dfrac{17}{12}\).\(\dfrac{15}{14}\)
= \(\dfrac{85}{56}\)

Chiều rộng của mảnh vườn hình chữ nhật là:
\(\dfrac{21}{4}\) : \(\dfrac{7}{3}\) = \(\dfrac{9}{4}\) (m)
Chu vi của mảnh vườn hìn chữ nhật là:
(\(\dfrac{21}{4}\) + \(\dfrac{9}{4}\)) x 2 = 15 (m)
Diện tích của mảnh vườn hình chữ nhật là:
\(\dfrac{21}{4}\) x \(\dfrac{9}{4}\) = \(\dfrac{189}{16}\) (m2)
b; Số tiền thu được khi trồng hoa để bán trên mảnh đất hình chữ nhật đó là:
80 000 x \(\dfrac{189}{16}\) = 945 000 (đồng)
KL...
Bài 5:
a, Chiều rộng mảnh vườn:
\(\dfrac{21}{4}:\dfrac{7}{3}=\dfrac{9}{4}\left(m\right)\)
Chu vi mảnh đất:
\(2\times\left(\dfrac{21}{4}+\dfrac{9}{4}\right)=15\left(m\right)\)
Diện tích mảnh đất:
\(\dfrac{21}{4}\times\dfrac{9}{4}=\dfrac{189}{16}\left(m^2\right)\)
b, Số tiền thu được khi bán hoa:
\(\dfrac{189}{16}\times80000=945000\left(đồng\right)\)

Gọi độ dài cạnh hình vuông là \(x\) (cm) (đk \(x\) > 0)
Theo bài ta khó: \(x^2\) = \(\dfrac{81}{16}\)
\(\left[{}\begin{matrix}x=\dfrac{9}{4}cm\\x=\dfrac{-9}{4}cm\end{matrix}\right.\)
Vì \(x\) > 0 nên \(x\) = \(\dfrac{9}{4}\) cm
Vậy số cần điền vào chỗ .. là \(\dfrac{9}{4}\)
b; Độ dài đường chéo thứ hai của hình thoi là bao nhiêu em? Thiếu dữ liệu em nhé?

a; \(\dfrac{-1}{3}\) \(\times\) \(\dfrac{5}{9}\) = \(\dfrac{-1\times5}{3\times9}\) = \(\dfrac{-5}{27}\)
b; \(\dfrac{-7}{3}\) \(\times\) (-6) = \(\dfrac{-7\times\left(-2\right)}{3}\) \(\times\) 3 = 14
c; \(\dfrac{22}{7}\) : \(\dfrac{11}{14}\) = \(\dfrac{22}{7}\) \(\times\) \(\dfrac{14}{11}\) = \(\dfrac{2\times11}{7}\) \(\times\) \(\dfrac{7\times2}{11}\) = 4
d; \(\dfrac{3}{5}\) + \(\dfrac{4}{7}\) \(\times\) \(\dfrac{14}{6}\) = \(\dfrac{3}{5}\) + \(\dfrac{4}{7}\) \(\times\) \(\dfrac{7\times2}{2\times3}\) = \(\dfrac{3}{5}\) + \(\dfrac{4}{3}\) = \(\dfrac{9}{15}\) + \(\dfrac{20}{15}\) = \(\dfrac{29}{15}\)
a) \(\dfrac{-1}{3}.\dfrac{5}{9}=\dfrac{-1.5}{3.9}=\dfrac{-5}{27}\)
b)\(\dfrac{-7}{3}.\left(-6\right)=\dfrac{\left(-7\right).\left(-6\right)}{3}=\dfrac{42}{3}=14\)
c)\(\dfrac{22}{7}:\dfrac{11}{14}=\dfrac{22}{7}.\dfrac{14}{11}=2.2=4\)
d)\(\dfrac{3}{5}+\dfrac{4}{7}.\dfrac{14}{6}=\dfrac{3}{5}+4.\dfrac{2}{6}=\dfrac{3}{5}+\dfrac{8}{6}=\dfrac{18}{30}+\dfrac{40}{30}=\dfrac{58}{30}=\dfrac{29}{15}\)
Chúc bạn học tốt!


Nếu mua hai gói thì giá của mỗi gói là:
\(90000:2=45000\left(đồng\right)\)
Nếu mua ba gói thì giá của mỗi gói là:
\(130000:3=43333\left(đồng\right)\)
Mà \(50000>45000>43333\) nên mẹ khuyên Mai nên mua 3 gói là rẻ nhất là đúng.
Nếu mua hai gói thì giá của mỗi gói là: 90000/2=45000
đồng
Nếu mua ba gói thì giá của mỗi gói là: 130000/3 đồng
Vì 130000/3< 45 000 < 50 000 đồng nên mua ba gói là rẻ nhất

Chu vi tam giác là:
\(\dfrac{5}{2}+\dfrac{18}{5}+\dfrac{25}{6}=\dfrac{75}{30}+\dfrac{108}{30}+\dfrac{125}{30}=\dfrac{308}{30}=\dfrac{154}{15}\left(cm\right)\)
Đáp số: \(\dfrac{154}{15}cm\)

số học sinh lớp 6 đó là:
1020x2/85=24(hs)
Số học sinh khối 6 của trường đó là:
24:2x25=300(hs)
vậy số học sinh khối 6 là 300 học sinh

Đây là dạng toán nâng cao chuyên đề về so sánh phân số, cấu trúc thi chuyên, thi học sinh giỏi, thi violympic. Hôm nay olm sẽ hướng dẫn em cách giải dạng này như sau.
Xét dãy số: 2; 3; 4;...; 2023
Dãy số trên là dãy số cách đều với khoảng cách là: 2 - 1 = 1
Số số hạng của dãy số trên là: (2023 - 2) : 1 + 1 = 2022
Vì \(\dfrac{3}{2^2}\) = \(\dfrac{3}{4}\) < 1 ; \(\dfrac{8}{3^2}\) = \(\dfrac{3^2-1}{3^2}\) < 1;...; \(\dfrac{2023^2-1}{2023^2}\) < 1
Vậy A là tổng của 2022 phân số mã mỗi phân số đều nhỏ hơn 1
⇒ A < 1 x 2022 = 2022 (1)
Mặt khác ta có:
A = \(\dfrac{3}{2^2}\) + \(\dfrac{8}{3^2}\) + \(\dfrac{15}{4^2}\) + \(\dfrac{2023^2-1}{2023^2}\)
A = 1 - \(\dfrac{1}{2^2}\) + 1 - \(\dfrac{1}{3^2}\) + ... + 1 - \(\dfrac{1}{2023^2}\)
A = (1 + 1 + 1+ ...+ 1) - (\(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\)+...+ \(\dfrac{1}{2023^2}\))
A = 2022 - (\(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\) + .... + \(\dfrac{1}{2023^2}\))
Đặt B = \(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\) + .... + \(\dfrac{1}{2023^2}\)
\(\dfrac{1}{2^2}\) < \(\dfrac{1}{1.2}\) = \(\dfrac{1}{1}\) - \(\dfrac{1}{2}\)
\(\dfrac{1}{3^2}\) < \(\dfrac{1}{2.3}\) = \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\)
\(\dfrac{1}{4^2}\) < \(\dfrac{1}{3.4}\) = \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\)
............................
\(\dfrac{1}{2023^2}\)< \(\dfrac{1}{2022.2023}\) = \(\dfrac{1}{2022}\) - \(\dfrac{1}{2023}\)
Cộng vế với vế ta có:
B < 1 - \(\dfrac{1}{2023}\)
⇒ - B > -1 + \(\dfrac{1}{2023}\)
⇒ A = 2022 - B > 2022 - 1 + \(\dfrac{1}{2023}\) = 2021 + \(\dfrac{1}{2023}\) ⇒ A > 2021 (2)
Kết hợp (1) và (2) ta có:
2021 < A < 2022
Vậy A không phải là số tự nhiên (đpcm)
A = 3. \(\dfrac{1}{1.2}\) - 5. \(\dfrac{1}{2.3}\) + 7. \(\dfrac{1}{3.4}\) + ... + 15. \(\dfrac{1}{7.8}\) -17 . \(\dfrac{1}{8.9}\)


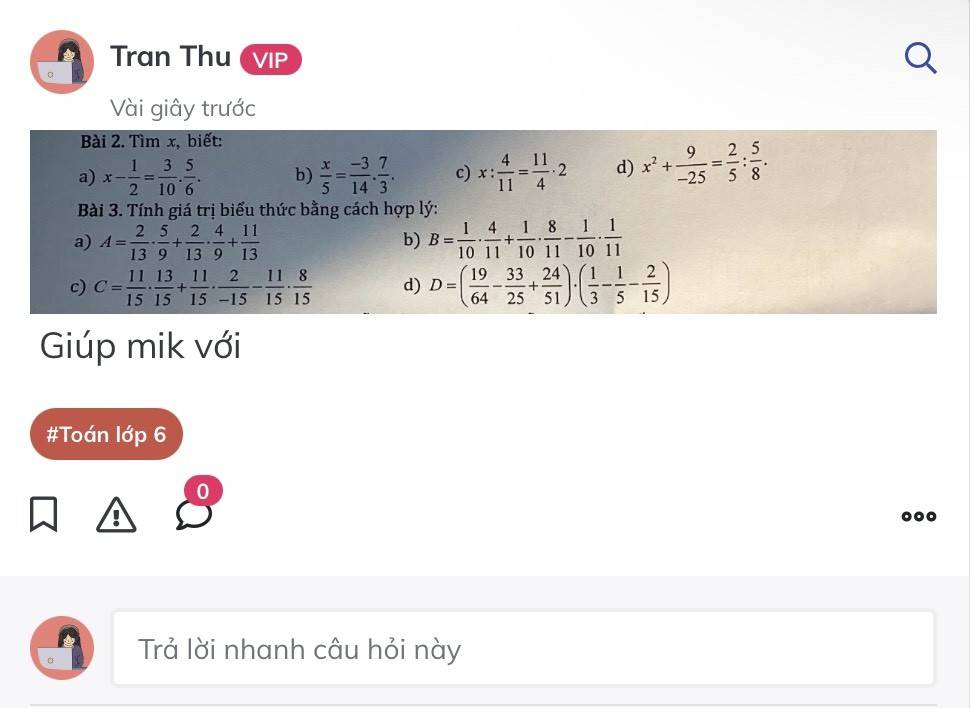
Bài 2:
a; \(x\) - \(\dfrac{1}{2}\) = \(\dfrac{3}{10}\).\(\dfrac{5}{6}\)
\(x\) - \(\dfrac{1}{2}\) = \(\dfrac{1}{4}\)
\(x\) = \(\dfrac{1}{4}\) + \(\dfrac{1}{2}\)
\(x\) = \(\dfrac{3}{4}\)
Vậy \(x\) = \(\dfrac{3}{4}\)
b; \(\dfrac{x}{5}\) = \(\dfrac{-3}{14}\) \(\times\) \(\dfrac{7}{3}\)
\(\dfrac{x}{5}\) = \(\dfrac{-1}{2}\)
\(x\) = \(\dfrac{-1}{2}\) \(\times\) 5
\(x\) = \(\dfrac{-5}{2}\)
Vậy \(x\) = \(\dfrac{-5}{2}\);
c; \(x\) : \(\dfrac{4}{11}\) = \(\dfrac{11}{4}\) \(\times\) 2
\(x\) : \(\dfrac{4}{11}\) = \(\dfrac{11}{2}\)
\(x\) = \(\dfrac{11}{2}\) \(\times\) \(\dfrac{4}{11}\)
\(x\) = 2
Vậy \(x\) = 2
d; \(x^2\) + \(\dfrac{9}{-25}\) = \(\dfrac{2}{5}\) : \(\dfrac{5}{8}\)
\(x^2\) - \(\dfrac{9}{25}\) = \(\dfrac{16}{25}\)
\(x^2\) = \(\dfrac{16}{25}\) + \(\dfrac{9}{25}\)
\(x^2\) = \(\dfrac{25}{25}\)
\(x^2\) = 1
\(\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
Vậy \(x\)\(\in\) {-1; 1}
Bài 3:
a; A = \(\dfrac{2}{13}\)\(\times\) \(\dfrac{5}{9}\)+ \(\dfrac{2}{13}\)\(\times\)\(\dfrac{4}{9}\) + \(\dfrac{11}{13}\)
A = \(\dfrac{2}{13}\) \(\times\)(\(\dfrac{5}{9}\) + \(\dfrac{4}{9}\)) + \(\dfrac{11}{13}\)
A = \(\dfrac{2}{13}\) \(\times\) \(\dfrac{9}{9}\) + \(\dfrac{11}{13}\)
A = \(\dfrac{2}{13}\) + \(\dfrac{11}{13}\)
A = 1
b; B = \(\dfrac{1}{10}\).\(\dfrac{4}{11}\) + \(\dfrac{1}{10}\).\(\dfrac{8}{11}\) - \(\dfrac{1}{10}\).\(\dfrac{1}{11}\)
B = \(\dfrac{1}{10}\) x (\(\dfrac{4}{11}\) + \(\dfrac{8}{11}\) - \(\dfrac{1}{11}\))
B = \(\dfrac{1}{10}\) x (\(\dfrac{12}{11}\) - \(\dfrac{1}{11}\))
B = \(\dfrac{1}{10}\) x \(\dfrac{11}{11}\)
B = \(\dfrac{1}{10}\)