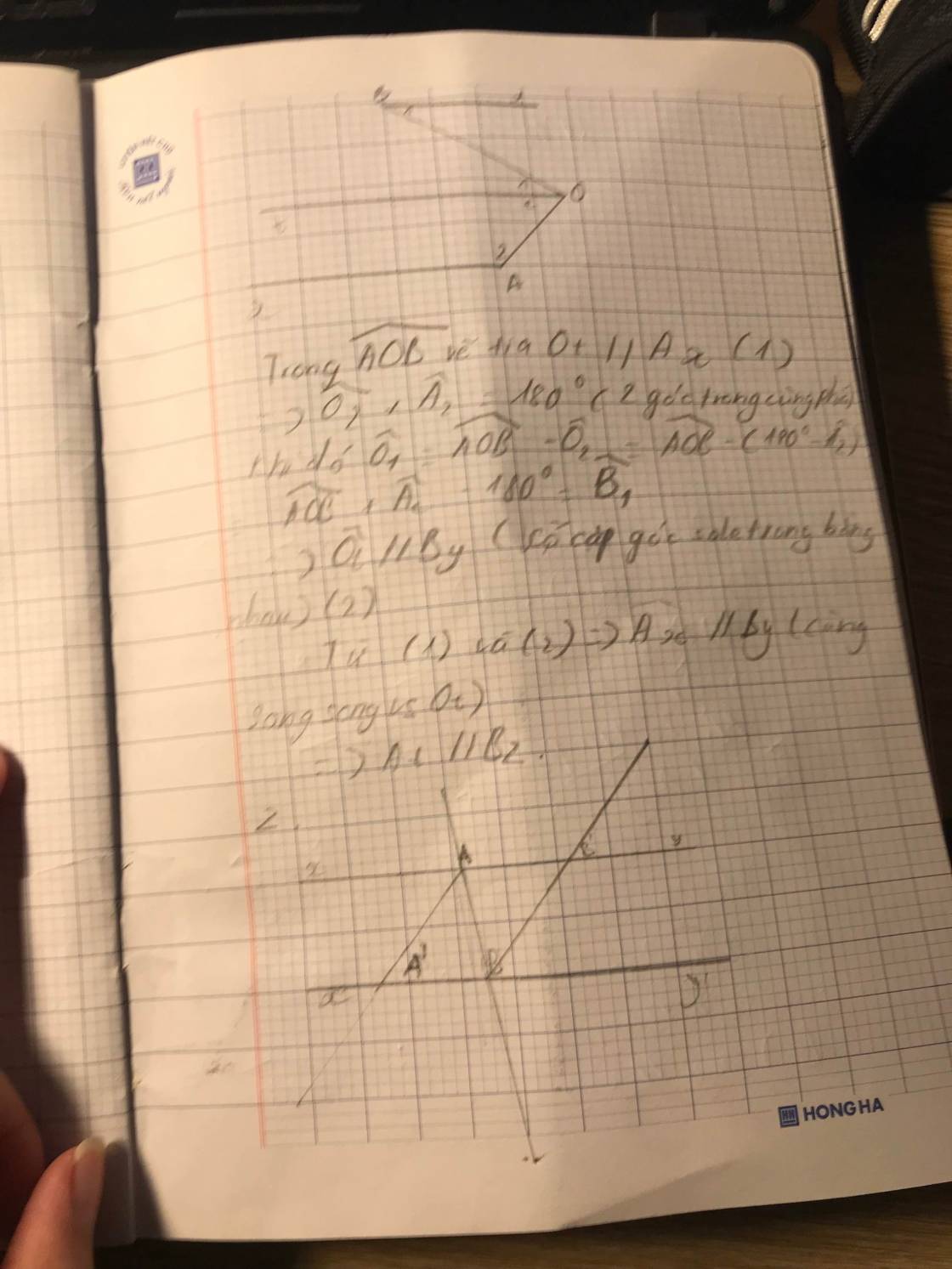
a, Ta có:  xy//x'y' nên xAB ^ = ABy' (hai góc so le trong).

AA' là tia phân giác của xAB nên A₁ = A₂ = 1/2 xAB 

BB' là tia phân giác của ABy'  nên B₁ = B₂ = 1/2 ABy'

Từ trên ta có A₂ = B₁

Mà hai góc ở vị trí so le trong, nên

=> AA' // BB/ (có 2 góc so le trong bằng nhau)

b, xy//x'y' nên A₁ = AA'B (2 góc so le trong)

AA'//BB' nên A₁ = AB'B(2 góc đồng vị)

Vậy AA'B = AB'B 

xx'yy'AB1212A'B'

a) x y / / x' y'xy//x′y′ nên \widehat{x A B}=\widehat{A B y'}xAB=ABy′​ (hai góc so le trong). (1)

AA'AA′ là tia phân giác của \widehat{xAB}xAB nên: \widehat{A_1}=\widehat{A_2}=\dfrac{1}{2} \widehat{xAB}A1​​=A2​​=21​xAB. (2)

BB'BB′ là tia phân giác của \widehat{ABy'}ABy′​ nên: \widehat{B_1}=\widehat{B_2}=\dfrac{1}{2} \widehat{ABy'}B1​​=B2​​=21​ABy′​. (3)

Từ (2) và (3) ta có: \widehat{A_2}=\widehat{B_1} .A2​​=B1​​.

Mà hai góc ở vị trí so le trong, nên từ (1), (2), (3) ta có: AA'AA′  //  BB'BB′ (có 2 góc so le trong bằng nhau).

b) x y / / x' y'xy//x′y′ nên \widehat{A_1}=\widehat{A A' B}A1​​=AA′B (hai góc so le trong).

AA' / / BB'AA′//BB′ nên \widehat{A_1}=\widehat{AB' B}A1​​=AB′B (hai góc đồng vị).

Vậy \widehat{AA' B}=\widehat{AB' B}AA′B=AB′B.

\(N=\frac{2}{3}x^2y^3\left(-\frac{6}{5}xy\right)\)

\(=\left(\frac{2}{3}.\frac{-6}{5}\right).\left(x^2.x\right).\left(y^3.y\right)\)

\(=-\frac{4}{5}x^3.y^4\)

TL

a)Xét tam giác ACD và tam giác ECD(đều là vuông)

         ECD=DCA(Vì CD là p/giác)

          CD là cạnh chung

⇒⇒tam giác ACD=tam giác ECD(cạnh huyền góc nhọn)

b)Vì tam giác ACD=tam giác ECD(cạnh huyền góc nhọn)

⇒⇒AD=DE(cạnh cặp tương ứng)

⇒⇒D cách đều hai mút của AE

⇒⇒CD là đường trung trực của AE

       Do đó CI⊥⊥AE

⇒⇒Tam giác CIE là tam giác vuông

c)Vì AD=DE(câu b)

Mà tam giác BDE là tam giác vuông(tại E)

⇒⇒DE<BD(cạnh góc vuông nhỏ hơn cạnh huyền)

⇒⇒AD<BD(đpcm)

d)Kéo dài BK cắt AC tại O

Vì BK⊥⊥CD(gt)

⇒⇒CK là đường cao thứ nhất của tam giác OBC(1)

Vì tam giác ABC vuông tại A

Nên BA⊥⊥AC

⇒⇒BA là đường cao thứ hai của tam giác OBC(2)

Theo đề bài ta có DE⊥⊥BC

Nên DE là đường cao thứ ba của tam giác OBC(3)

      Từ (1),(2) và (3) suy ra:

Ba đường cao giao nhau tại một điểm trùng với điểm D

⇒⇒ 3 đường thẳng AC;DE;BK đồng quy(đpcm)

Học tốt nha ^^

`Answer:`

Cho \widehat{AOB}+\widehat{A_2} -180^{\circ} = \widehat{B_1}AOB+A2​​−180∘=B1​​. Chứng minh rằng $Ax$ // $By$.

Trong \widehat{A O B}AOB dựng tia $Ot$ // $Ox$. (1)

Suy ra \widehat{O}_{2}+\widehat{A}_{2}=180^{\circ}O2​+A2​=180∘ (2 góc trong cùng phía).

Khi đó \widehat{O}_{1} =\widehat{A O B}-\widehat{O}_{2} =\widehat{A O B}-\left(180^{\circ}-\widehat{A}_{2}\right) =\widehat{A O B}+\widehat{A}_{2}-180^{\circ} =\widehat{B}_{1}O1​=AOB−O2​=AOB−(180∘−A2​)=AOB+A2​−180∘=B1​

$\Rightarrow Ot$ // $By$ (vì có cặp góc so le trong bằng nhau). (2)

Từ (1) và (2) suy ra $Ax$ // $By$ (vì cùng song song với $Ot$ ).

Vậy $At$ // $Bz$.