Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tổng 3 số đó là:
37 x 3= 111
Vì 111 = 100 + 10 + 1
Mà 3 số này là 3 số tự nhiên nhỏ nhất có 1 chữ số (khác 0), nhỏ nhất có 2 chữ số và nhỏ nhất có 3 chữ số
Nên 3 số cần tìm chắc chắn là: 1; 10 và 100

a, Số mét vải xanh cửa hàng có:
1305: 3= 435(m)
Số mét vải trắng cửa hàng có:
1305:5= 261(m)
Số mét vải hoa cửa hàng có:
1305 - (435+261)= 609(m)
Đáp số: 609 mét vải
Bài 2:
Thứ 2 tuần trước là ngày 18/3
Thứ 2 tuần trước đến thứ 2 tuần này là 7 ngày, thứ 2 tuần này đến thứ 2 tuần sau là 7 ngày, thứ 2 tuần sau đến thứ 4 tuần sau là 2 ngày
Khoảng cách giữa thứ 2 tuần trước đến thứ 4 tuần sau là:
7+7+2=16(ngày)
Thứ tư tuần sau là:
18+16=34 > 31
Vì: 34-31=3
Vậy thứ tư tuần sau là ngày 3 tháng 4

ĐKXĐ: \(x\ne0\)
- Với \(x< 0\Rightarrow\left\{{}\begin{matrix}\sqrt{x^2+1}+3>0\\\dfrac{1}{x}-3< 0\Rightarrow\left(\dfrac{1}{x}-3\right)\left(\sqrt{9x^2-6x+2}+3\right)< 0\end{matrix}\right.\)
\(\Rightarrow\) Phương trình vô nghiệm
- Với \(x\ge\dfrac{1}{3}\) tương tự ta có \(\dfrac{1}{x}-3\le0\Rightarrow\left\{{}\begin{matrix}VT>0\\VT\le0\end{matrix}\right.\) nên pt vô nghiệm
- Với \(0< x< \dfrac{1}{3}\)
\(\Rightarrow x\sqrt{x^2+1}+3x=\left(1-3x\right)\left(\sqrt{\left(1-3x\right)^2+1}+3\right)\)
Đặt \(1-3x=y>0\)
\(\Rightarrow x\sqrt{x^2+1}+3x=y\left(\sqrt{y^2+1}+3\right)\)
\(\Leftrightarrow x\sqrt{x^2+1}-y\sqrt{y^2+1}+3\left(x-y\right)=0\)
\(\Leftrightarrow\dfrac{x^2\left(x^2+1\right)-y^2\left(y^2+1\right)}{x\sqrt{x^2+1}+y\sqrt{y^2+1}}+3\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(\dfrac{\left(x+y\right)\left(x^2+y^2\right)+x+y}{x\sqrt{x^2+1}+y\sqrt{y^2+1}}+3\right)=0\) (1)
Do \(\dfrac{\left(x+y\right)\left(x^2+y^2\right)+x+y}{x\sqrt{x^2+1}+y\sqrt{y^2+1}}+3>0;\forall x;y>0\)
\(\left(1\right)\Leftrightarrow x-y=0\Leftrightarrow x-\left(1-3x\right)=0\)
\(\Rightarrow x=\dfrac{1}{4}\)

b.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1x_2=-1\end{matrix}\right.\)
\(T=\dfrac{3\left|x_1-x_2\right|}{x_1^2x_2+x_1x_2^2}=\dfrac{3\sqrt{\left(x_1-x_2\right)^2}}{x_1x_2\left(x_1+x_2\right)}=\dfrac{3\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}}{x_1x_2\left(x_1+x_2\right)}\)
\(=\dfrac{3\sqrt{\left(-3\right)^2-4.\left(-1\right)}}{-1.\left(-3\right)}=\sqrt{13}\)

\(P=x^2-x\left(15-x\right)+\left(15-x\right)^2=3x^2-45x+225\)
\(P=3x\left(x-9\right)+225\)
Do \(0\le x\le6\Rightarrow x-9< 0\Rightarrow3x\left(x-9\right)\le0\)
\(\Rightarrow P\le225\)
\(P_{max}=225\) khi \(\left(x;y\right)=\left(0;15\right)\)
\(P=3x^2-45x+162+63=3\left(9-x\right)\left(6-x\right)+63\)
Do \(x\le6\Rightarrow\left\{{}\begin{matrix}9-x>0\\6-x\ge0\end{matrix}\right.\) \(\Rightarrow3\left(9-x\right)\left(6-x\right)\ge0\)
\(\Rightarrow P\ge63\)
\(P_{min}=63\) khi \(\left(x;y\right)=\left(6;9\right)\)


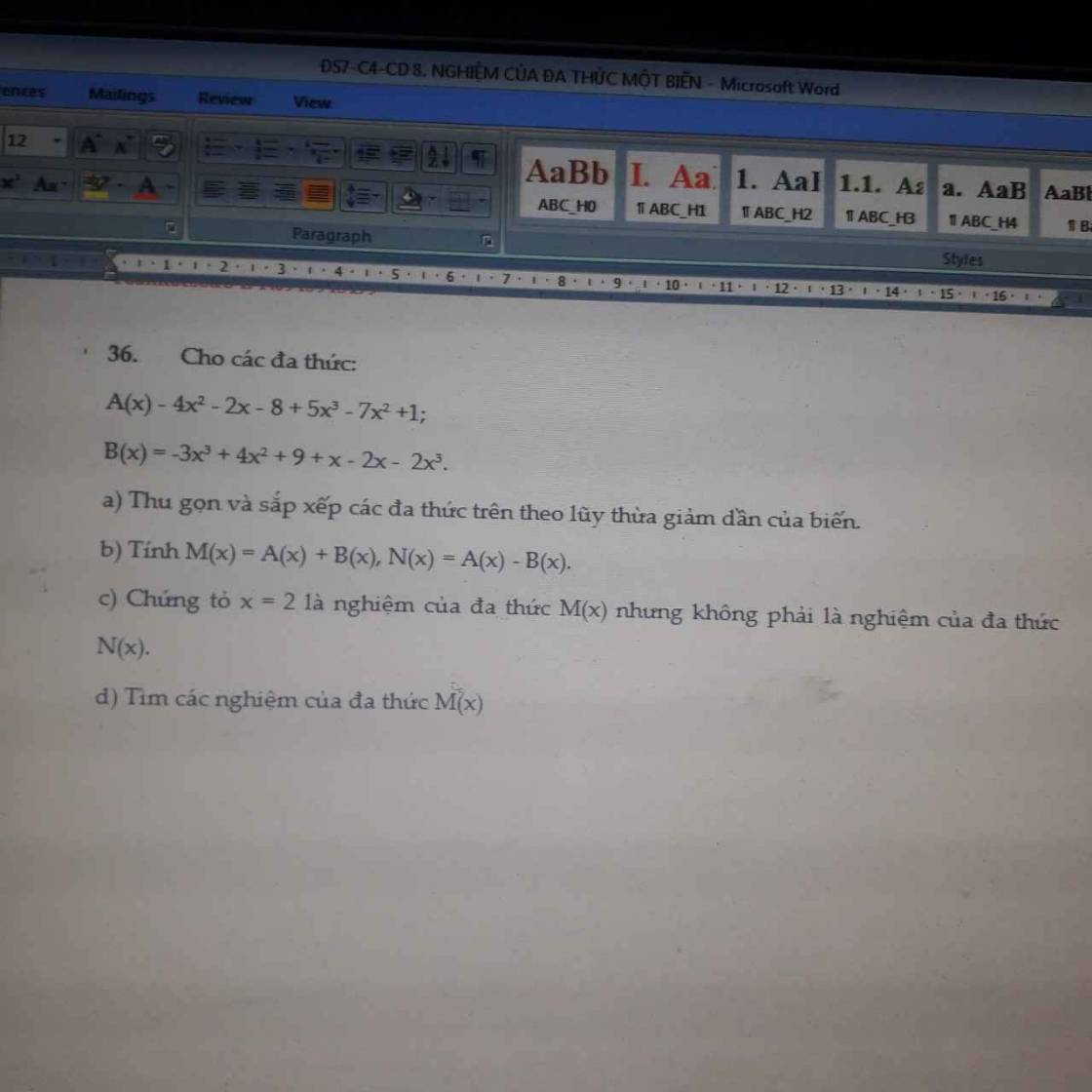
a)
\(A\left(x\right)=4x^2-2x-8+5x^3-7x^2+1\\ \text{ }=5x^3-\left(7x^2-4x^2\right)-2x-\left(8-1\right)\\ \text{ }=5x^3-3x^2-2x-7\)
\(B\left(x\right)=-3x^3+4x^2+9+x-2x-2x^3\\ \text{ }=\left(-3x^3-2x^3\right)+4x^2+\left(x-2x\right)+9\\ \text{ }=-5x^3+4x^2-x+9\)
b)
\(M\left(x\right)=A\left(x\right)+B\left(x\right)\\ \text{ }=\left(5x^3-3x^2-2x-7\right)+\left(-5x^3+4x^2-x+9\right)\\ \text{ }=5x^3-3x^2-2x-7-5x^3+4x^2-x+9\\ \text{ }=\left(5x^3-5x^3\right)+\left(4x^2-3x^2\right)-\left(2x-x\right)+\left(9-7\right)\\ \text{ }=x^2-x+2\)
\(N\left(x\right)=A\left(x\right)-B\left(x\right)\\ \text{ }=\left(5x^3-3x^2-2x-7\right)-\left(-5x^3+4x^2-x+9\right)\\ \text{ }=5x^3-3x^2-2x-7+5x^3-4x^2+x-9\\ \text{ }=\left(5x^3+5x^3\right)-\left(3x^2+4x^2\right)-\left(2x-x\right)-\left(7+9\right)\\ \text{ }=10x^3-7x^2-x-16\)