
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đây là dạng toán nâng cao chuyên đề chi diện tích hình ghép. Cấu trúc thi chuyên, thi học sinh giỏi các cấp, thi violympic. Hôm nay Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Ta có hình minh họa
Chu vi của cái hồ hình bán nguyệt là chu vi của nửa hình tròn và đường kính của nó.
Chu vi của cái hồ hình bán nguyệt bằng:
3,14 x \(\dfrac{1}{2}\) + 1 = 2,57 (lần đường kính của hồ)
Đường kính của hồ là:
30,84 : 2,57 = 12 (m)
Diện tích của cái hồ hình bán nguyệt là:
12 x 12 x 3,14 : 4 = 113,04 (m2)
Đáp số: 113,04 (m2)

Olm chào em, đây là dạng toán nâng cao chuyên đề chu vi diện tích hình ghép. Cấu trúc thi chuyên, thi học sinh giỏi các cấp, thi violympic. Hôm nay, Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Vì chỉ mở rộng về một phía nên khi đó, phần đất mở rộng sẽ là một hình vuông mới có cạnh bằng cạnh của hình vuông ban đầu và có diện tích là 36m2
Vì 36 = 6 x 6
Vậy cạnh của cái ao hình vuông ban đầu là 6m
Chiều rộng của cái ao lúc sau chính là cạnh của hình vuông lúc đầu và bằng 6m
Chiều dài của cáo ao lúc sau là: 6 x 2 = 12(m)
Chu vi cả cái ao sau khi mở rộng là: (12 + 6) x 2 = 36 (m)
Đáp số: 36 m

\(x^4+ax^2+b⋮x^2-x+1\)
=>\(x^4-x^3+x^2+x^3-x^2+x+ax^2-ax+a+x\left(a-1\right)-a+b⋮x^2-x+1\)
=>\(\left\{{}\begin{matrix}a-1=0\\-a+b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=1\\b=a=1\end{matrix}\right.\)

\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\dfrac{1}{n^2}< \dfrac{1}{n-1}-\dfrac{1}{n}\)
Do đó: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n-1}-\dfrac{1}{n}=1-\dfrac{1}{n}\)
=>\(A=\dfrac{1}{1^2}+\dfrac{1}{2^2}+...+\dfrac{1}{n^2}< 2-\dfrac{1}{n}< 2\)
=>A<2
mà A>1
nên 1<A<2
=>A không là số tự nhiên
ta có
1/2^2 =1/2.2 < 1/1.2 (do 1/2.2 = 1/4 <1/2)
1/3^2 = 1/3.3 <1/2.3
1/4^2= 1/4. 4 <1/3.4
...... (làm tương tự thế)
1/n^2 =1/n.n < 1/(n-1).n
suy ra 1/2^2 + 1/3^2 + 1/4^2 +....+1/n^2 < 1/1.2 + 1/2.3 + 1/3.4 +...+1/n.(n+1)
ta có 1/1.2 + 1/2.3 + 1/3.4 + ... +1/(n-1).n
=1/1 - 1/2 + 1/2 - 1/3 + 1/3 - 1/4 + .... +1/n-1 -1/n
=1/1 - 1/n (1/n-1)triệt tiêu phía trước)
suy ra 1/2^2 + 1/3^2 + 1/4^2 + ...+1/n^2 < 1-1/n <1
mà 1/2^2 + 1/3^2 + ...+1/n^2 >0
suy ra 0<1/2^2 +1/3^2+...+1/n^2<1
suy ra 1/2^2 +1/3^2 +....+1/n^2 ko là số tự nhiên với số tự nhiên n>2
bạn đừng ghi cái ngoặc nhé

1: \(\dfrac{2x+1}{x\sqrt{x}-1}-\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
\(=\dfrac{2x+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
\(=\dfrac{2x+1-\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{1}{\sqrt{x}-1}\)
\(\left(\dfrac{1+x\sqrt{x}}{1+\sqrt{x}}-\sqrt{x}\right)\)
\(=\dfrac{\left(1+\sqrt{x}\right)\left(1-\sqrt{x}+x\right)}{1+\sqrt{x}}-\sqrt{x}\)
\(=1-\sqrt{x}+x-\sqrt{x}=x-2\sqrt{x}+1=\left(\sqrt{x}-1\right)^2\)
\(B=\left(\dfrac{2x+1}{x\sqrt{x}-1}-\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\right)\left(\dfrac{1+x\sqrt{x}}{1+\sqrt{x}}-\sqrt{x}\right)+\dfrac{2-2\sqrt{x}}{\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}-1}+\dfrac{2-2\sqrt{x}}{\sqrt{x}}\)
\(=\sqrt{x}-1+\dfrac{2-2\sqrt{x}}{\sqrt{x}}=\dfrac{x-\sqrt{x}+2-2\sqrt{x}}{\sqrt{x}}\)
\(=\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}=\left(\sqrt{x}-1\right)\cdot\dfrac{\left(\sqrt{x}-2\right)}{\sqrt{x}}\)
2:
a:
Để B=0 thì \(\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\sqrt{x}}=0\)
=>\(\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)=0\)
=>\(\left[{}\begin{matrix}x=1\left(loại\right)\\x=4\left(nhận\right)\end{matrix}\right.\)
b: \(B+\dfrac{3\sqrt{x}-4}{\sqrt{x}}< =0\)
=>\(\dfrac{x-3\sqrt{x}+2+3\sqrt{x}-4}{\sqrt{x}}< =0\)
=>x-2<=0
=>x<=2
kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0< x< =2\\x\ne1\end{matrix}\right.\)
3: Để B là số nguyên thì \(x-3\sqrt{x}+2⋮\sqrt{x}\)
=>\(\sqrt{x}\left(\sqrt{x}-3\right)+2⋮\sqrt{x}\)
=>\(2⋮\sqrt{x}\)
=>\(\sqrt{x}\in\left\{1;2\right\}\)
=>\(x\in\left\{1;4\right\}\)
Kết hợp ĐKXĐ, ta được: x=4

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
=>\(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)
=>\(BA^2=BH\cdot BC\)
b: Xét ΔCED vuông tại E và ΔCHA vuông tại H có
\(\widehat{ECD}\) chung
Do đó: ΔCED~ΔCHA
=>\(\dfrac{CE}{CH}=\dfrac{CD}{CA}\)
=>\(\dfrac{CE}{CD}=\dfrac{CH}{CA}\)
=>\(CE\cdot CA=CD\cdot CH\)
Xét ΔCEH và ΔCDA có
\(\dfrac{CE}{CD}=\dfrac{CH}{CA}\)
\(\widehat{ECH}\) chung
Do đó: ΔCEH~ΔCDA
=>\(\widehat{CHE}=\widehat{CAD}\)
mà \(\widehat{CAD}+\widehat{BAD}=\widehat{BAC}=90^0\)
và \(\widehat{CHE}+\widehat{AHE}=\widehat{CHA}=90^0\)
nên \(\widehat{BAD}=\widehat{AHE}\)
Xét ΔBAD và ΔAHE có
\(\widehat{BAD}=\widehat{AHE}\)
\(\widehat{ABD}=\widehat{HAE}\)
Do đó: ΔBAD~ΔAHE
c: ta có: \(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}=90^0\)
\(\widehat{BDA}+\widehat{HAD}=90^0\)(ΔHAD vuông tại H)
mà \(\widehat{BAD}=\widehat{BDA}\)(ΔBAD cân tại B)
nên \(\widehat{CAD}=\widehat{HAD}\)
=>AD là phân giác của góc HAC
Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
\(\widehat{HAD}=\widehat{EAD}\)
Do đó: ΔAHD=ΔAED
=>AH=AE
=>ΔAHE cân tại A
=>AD\(\perp\)HE
mà HE//AF
nên AD\(\perp\)AF
=>AF là phân giác góc ngoài tại A của ΔAHC
Xét ΔAHC có AF là phân giác ngoài
nên \(\dfrac{FH}{FC}=\dfrac{AH}{AC}\left(1\right)\)
Xét ΔAHC có AD là phân giác
nên \(\dfrac{AH}{AC}=\dfrac{DH}{DC}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{FH}{FC}=\dfrac{DH}{DC}\)
=>\(FH\cdot DC=DH\cdot FC\)


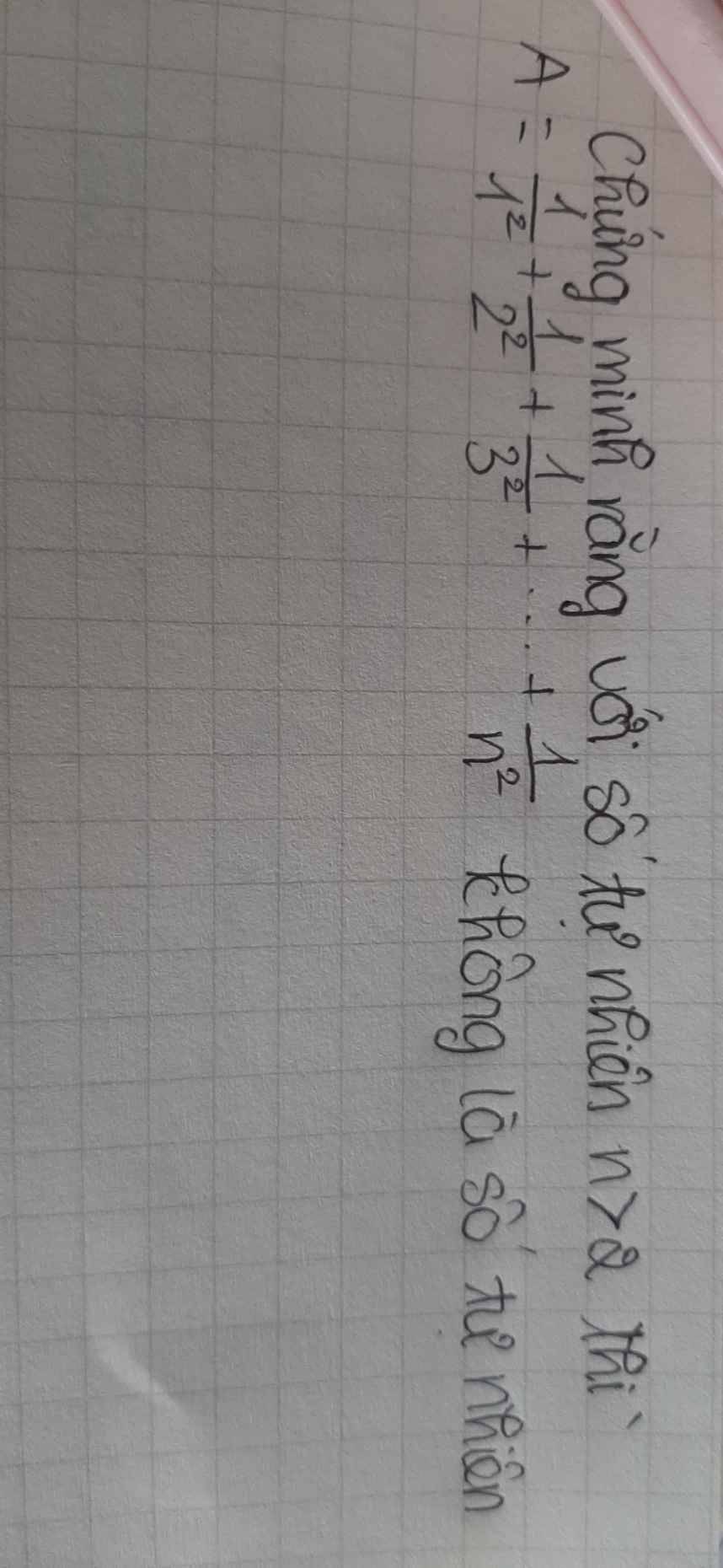

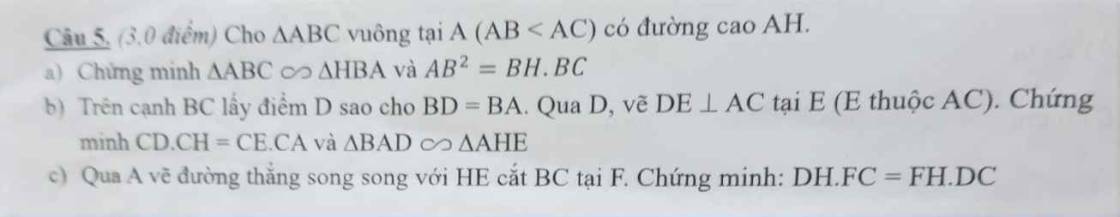
a) Trên tia Ox, do OM < ON (4 cm < 8 cm) nên điểm M nằm giữa hai điểm O và N
\(\Rightarrow OM+MN=ON\)
\(\Rightarrow MN=ON-OM\)
\(=8-4\)
\(=4\left(cm\right)\)
b) Do điểm M nằm giữa hai điểm O và N
Và \(OM=MN=4\left(cm\right)\)
\(\Rightarrow M\) là trung điểm của đoạn thẳng ON
c) Sửa đề, lấy điểm I sao cho NI = 2 cm
Giải
Trên tia \(NO\), do \(NI< NM\left(2cm< 4cm\right)\) nên điểm \(I\) nằm giữa hai điểm M và N
\(\Rightarrow MI+NI=MN\)
\(\Rightarrow MI=MN-NI\)
\(=4-2\)
\(=2\left(cm\right)\)
test