
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C D E O G F H K I
a/
Ta có
\(\widehat{OAC}=\widehat{OGC}=90^o\)
=> A và G cùng nhìn OC dưới hai góc bằng nhau và bằng \(90^o\) => A và C thuộc đường trong đường kính OC => ACGO nội tiếp
Xét tg vuông OGF và tg vuông CAF có chung \(\widehat{AFC}\)
=> tg OGF đồng dạng với tg CAF (g.g.g)
\(\Rightarrow\dfrac{GO}{AC}=\dfrac{FO}{FC}\Rightarrow GO.FC=AC.FO\)
b/
Xét tứ giác nội tiếp ACGO có
\(\widehat{OCG}=\widehat{OAG}\) (góc nt cùng chắn cung GO)
EK//CO (gt) \(\Rightarrow\widehat{OCG}=\widehat{HEG}\) (góc so le trong)
\(\Rightarrow\widehat{OAG}=\widehat{HEG}\)
=> A và E cùng phía với GH; A và E cùng nhìn GH dưới 2 góc bằng nhau => AGHE là tứ giác nội tiếp
\(\widehat{BAE}=\widehat{HGE}\) (góc nt cùng chắn cung HE
Xét (O) có
\(\widehat{BAE}=\widehat{BDE}\) (Góc nt cùng chắn cung BE)
\(\Rightarrow\widehat{HGE}=\widehat{BDE}\) mà 2 góc trên ở vị trí đồng vị =>GH//KD (1)
Ta có
\(OG\perp DE\Rightarrow GD=GE\) (trong đường tròn đường thẳng đi qua tâm và vuông góc với dây cung thì chia đôi dây cung) (2)
Xét tg DEK từ (1) và (2) => HK=HE (trong tam giác đường thẳng // với 1 cạnh và đi qua trung điểm của 1 cạnh thì đi qua trung điểm cạnh còn lại)

a: \(B=\dfrac{\sqrt{x}}{\sqrt{x}-5}-\dfrac{10\sqrt{x}}{x-25}-\dfrac{5}{\sqrt{x}+5}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+5\right)-10\sqrt{x}-5\left(\sqrt{x}-5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\)
\(=\dfrac{x+5\sqrt{x}-10\sqrt{x}-5\sqrt{x}+25}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}=\dfrac{x-10\sqrt{x}+25}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\)
\(=\dfrac{\left(\sqrt{x}-5\right)^2}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}=\dfrac{\sqrt{x}-5}{\sqrt{x}+5}\)
b: \(B=\dfrac{1}{2}\)
=>\(\dfrac{\sqrt{x}-5}{\sqrt{x}+5}=\dfrac{1}{2}\)
=>\(2\sqrt{x}-10=\sqrt{x}+5\)
=>\(\sqrt{x}=15\)
=>x=225(nhận)

a: \(x^2-2\left(m+1\right)x+4m=0\left(1\right)\)
\(\text{Δ}=\left[-2\left(m+1\right)\right]^2-4\cdot1\cdot4m\)
\(=4m^2+8m+4-16m=4m^2-8m+4=\left(2m-2\right)^2\)>=0 với mọi m
=>Phương trình (1) luôn có nghiệm
b: Vì Δ>=0 nên phương trình (1) không bao giờ vô nghiệm
=>\(m\in\varnothing\)
c: Để (1) có nghiệm kép thì Δ=0
=>2m-2=0
=>m=1
d: Để (1) có hai nghiệm phân biệt thì Δ>0
=>\(2m-2\ne0\)
=>\(m\ne1\)

\(\text{Δ}=4^2-4\cdot1\cdot m=-4m+16\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>-4m+16>0
=>-4m>-16
=>m<4
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-4\\x_1x_2=\dfrac{c}{a}=m\end{matrix}\right.\)
\(x_1^2+x_2^2=6x_1x_2\)
=>\(\left(x_1+x_2\right)^2-8x_1x_2=0\)
=>\(\left(-4\right)^2-8m=0\)
=>16-8m=0
=>8m=16
=>m=2(nhận)

1: Khi m=2 thì y=2x+1-2=2x-1
Phương trình hoành độ giao điểm là:
-4x+5=2x-1
=>-4x-2x=-1-5
=>-6x=-6
=>x=1
Thay x=1 vào y=-4x+5, ta được:
\(y=-4\cdot1+5=1\)
Vậy: Tọa độ giao điểm là A(1;1)
2: Phương trình hoành độ giao điểm là:
\(x^2=2x+1-m\)
=>\(x^2-2x+m-1=0\)
a=1; b=-2; c=m-1
Để (P) cắt (d) tại hai điểm nằm về hai phía so với trục Oy thì a*c<0
=>1(m-1)<0
=>m-1<0
=>m<1

a: Thay x=2 và y=500 vào y=ax+b, ta được:
\(a\cdot2+b=500\)(1)
1g=1000mg
Thay x=5 và y=1000 vào y=ax+b, ta được:
\(a\cdot5+b=1000\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=500\\5a+b=1000\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-3a=-500\\2a+b=500\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=\dfrac{500}{3}\\b=500-\dfrac{1000}{3}=\dfrac{500}{3}\end{matrix}\right.\)
b: a=500/3; b=500/3
=>\(y=\dfrac{500}{3}x+\dfrac{500}{3}\)
2g=2000mg
Thay y=2000 vào y=500/3x+500/3, ta được:
\(\dfrac{500}{3}x+\dfrac{500}{3}=2000\)
=>\(\dfrac{500}{3}x=2000-\dfrac{500}{3}=\dfrac{5500}{3}\)
=>x=11
=>Đứa trẻ đó 11 tuổi

\(\left\{{}\begin{matrix}x+y=3\\2x-y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=3\\3x=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{3}+y=3\\x=\dfrac{4}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=3-\dfrac{4}{3}\\x=\dfrac{4}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{5}{3}\\x=\dfrac{4}{3}\end{matrix}\right.\)
Vậy: ...
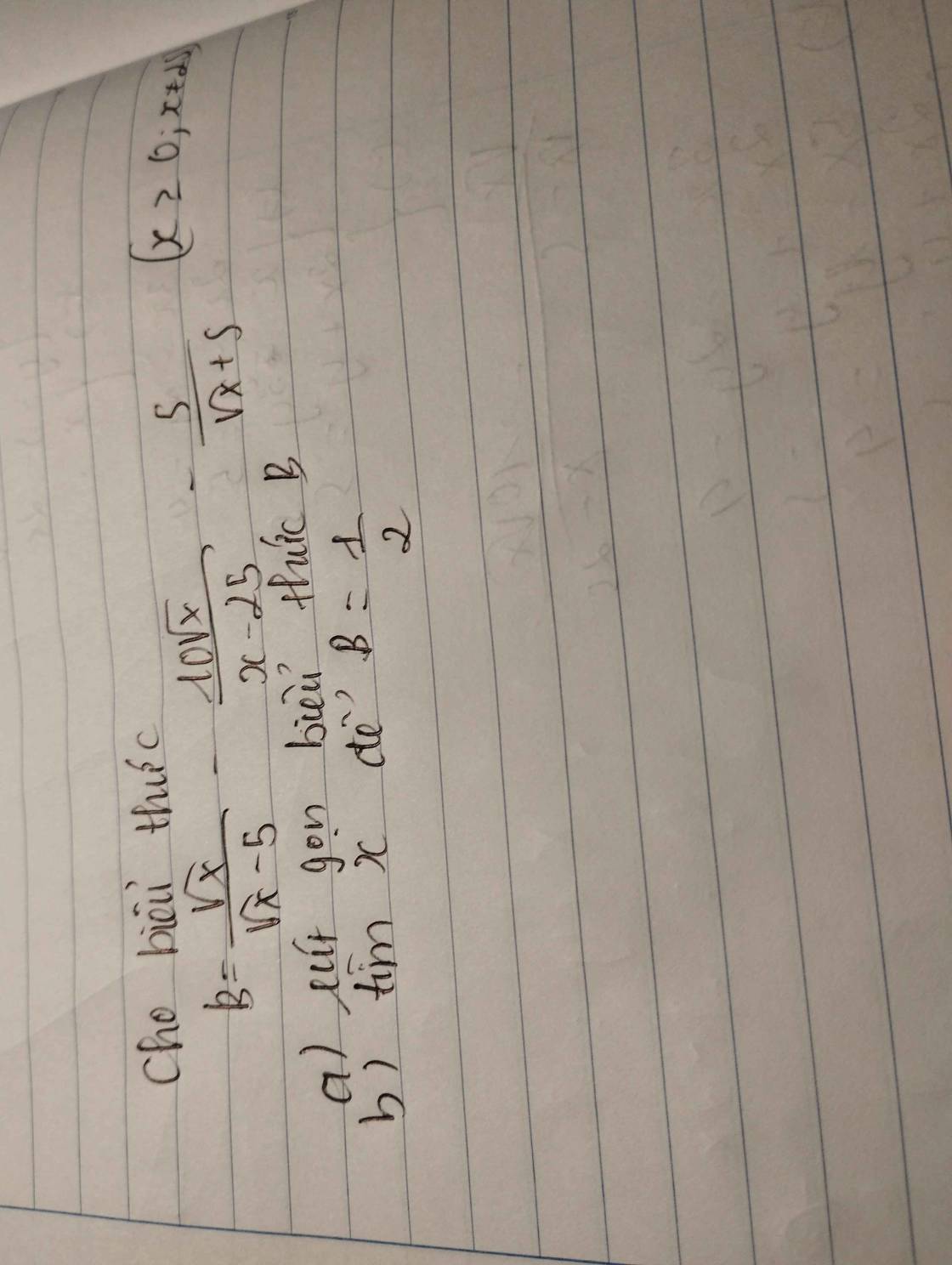


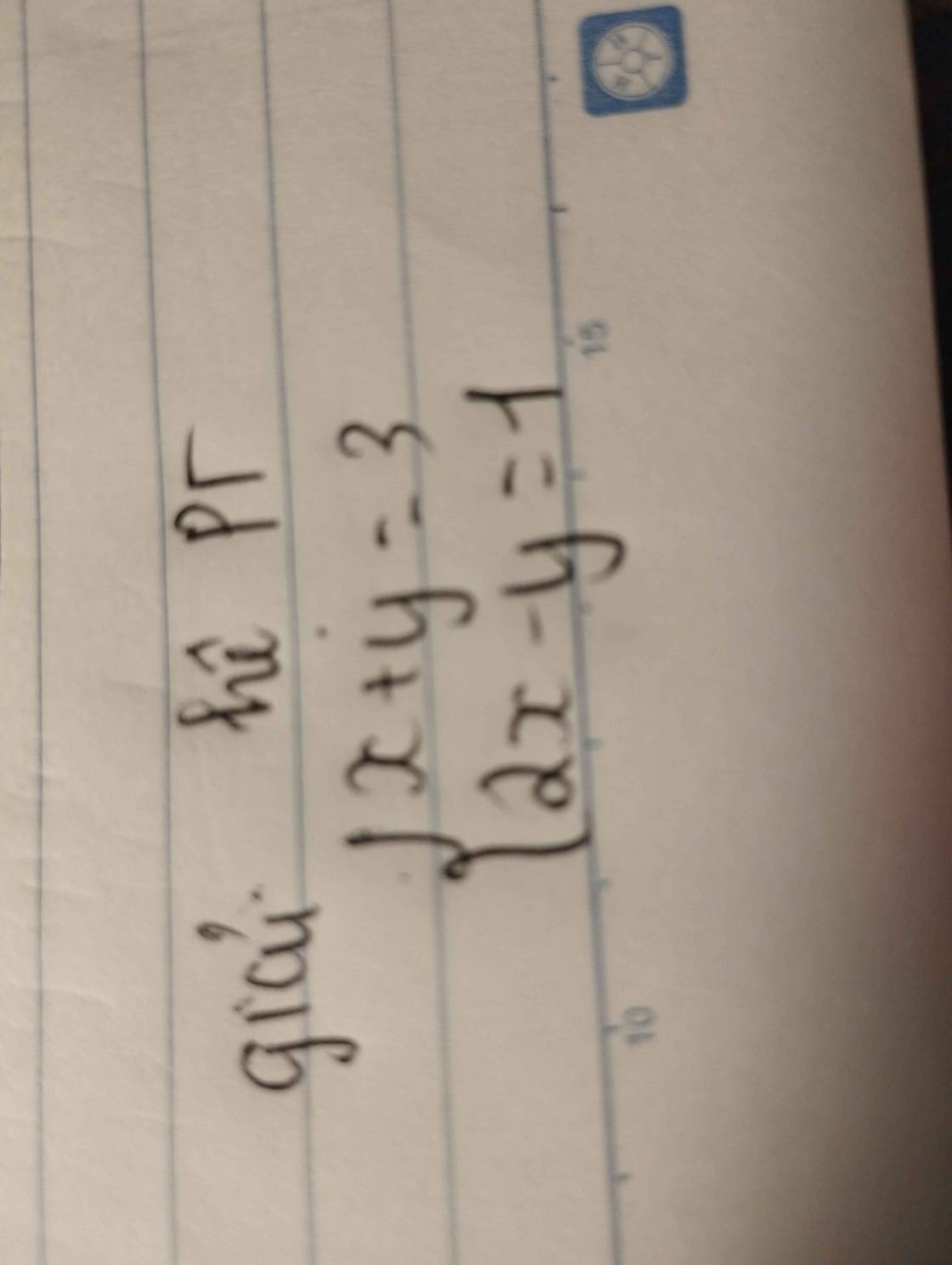
Câu III:
1: ĐKXĐ: y>-3/2
\(\left\{{}\begin{matrix}2\left|x\right|+\dfrac{1}{\sqrt{2y+3}}=11\\-\left|x\right|+\dfrac{3}{\sqrt{2y+3}}=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2\left|x\right|+\dfrac{1}{\sqrt{2y+3}}=11\\-2\left|x\right|+\dfrac{6}{\sqrt{2y+3}}=-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{7}{\sqrt{2y+3}}=7\\2\left|x\right|+\dfrac{1}{\sqrt{2y+3}}=11\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{2y+3}=1\\2\left|x\right|=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2y+3=1\\\left|x\right|=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x\in\left\{5;-5\right\}\end{matrix}\right.\left(nhận\right)\)
2: a: Phương trình hoành độ giao điểm là:
\(2x^2=x+m^2+6\)
=>\(2x^2-x-m^2-6=0\)
\(a\cdot c=2\cdot\left(-m^2-6\right)=-2m^2-12< =-12< 0\forall m\)
=>(P) luôn cắt (d) tại hai điểm phân biệt
Câu IV:
2: Ta có: HQ//AC
BE\(\perp\)AC
Do đó: QH\(\perp\)BE tại H
Ta có: HP//AB
CF\(\perp\)AB
Do đó: HP\(\perp\)CF tại H
Xét ΔHQB vuông tại Q và ΔHPC vuông tại P có
\(\widehat{QBH}=\widehat{PCH}\left(=90^0-\widehat{BAE}\right)\)
Do đó: ΔHQB~ΔHPC
Gọi K là giao điểm của AO với (O)
=>AK là đường kính của (O)
Xét (O) có
ΔACK nội tiếp
AK là đường kính
Do đó: ΔACK vuông tại C
Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
\(\widehat{AKC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ABC}=\widehat{AKC}\)
Xét ΔADB vuông tại D và ΔACK vuông tại C có
\(\widehat{ABD}=\widehat{AKC}\)
Do đó: ΔADB~ΔACK
=>\(\widehat{BAD}=\widehat{KAC}\)
=>\(\widehat{BAD}=\widehat{OAC}\)