cho: a/c=c/b. Chứng minh rằng: a^2+c^2 = a b^2+c^2 b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!


x : 2 = y : (-5)
 Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
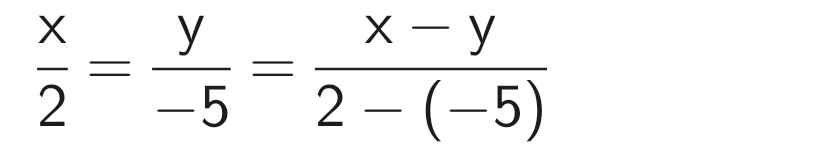

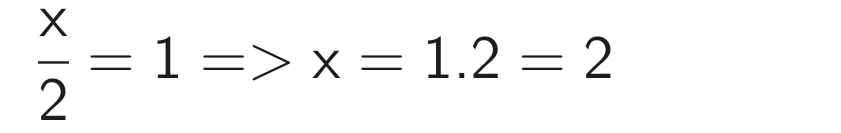
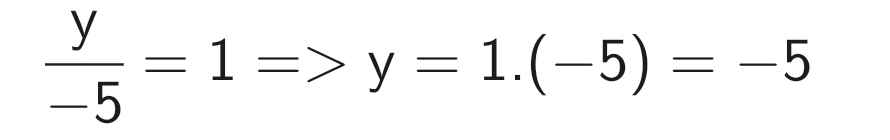
Vậy x = 2; y = -5
Vì 2 và (-5) nguyên tố cùng nhau nên ước chung của 2 và (-5) chỉ có thể là 1 hoặc -1
TH1: (2,-5) = 1
\(\rArr\) x : 2 = 1 \(\rArr\) x=2
y : (-5) = 1 \(\rArr\) y=(-5)
THỬ: 2 + (-5) = 7 (t/mãn)
TH2: (2,-5) = -1
\(\rArr\) x : 2 = -1 \(\rArr\) x=-2
y : (-5) = -1 \(\rArr\) y=5
THỬ: (-2) + 5 = 3 (không thoả mãn)
Vậy x=-2 và y=5

3 x (\(x+11\)) = 2 x (14 - \(x\))
3\(x\) + 33 = 28 - 2\(x\)
3\(x\) + 2\(x\) = 28 - 33
5\(x\) = -5
\(x=-5:5\)
\(x=-1\)
Vậy \(x=-1\)

Giải toán bằng cách lập phương trình:
Gọi chiều dài là \(x\) (m) \(x>0\) ; Chiều rộng là: \(\frac57x\) (m)
Chu vi của hình chữ nhật là: (\(x+\frac57x\)) x 2 = 120
\(x+\frac57x\) = 120 : 2
\(x\left(1+\frac57\right)\) = 60
\(\frac{x.12}{7}\) = 60
\(x=60:\frac{12}{7}\)
\(x=35\)
Chiều dài là 35 m; Chiều rộng là 35 x \(\frac57\) = 25 (m)
Kết luận: Chiều dài của hình chữ nhật là 35m; Chiều rộng hình chữ nhật là: 25 m
Gọi chiều rộng, chiều dài vườn hoa lần lượt là a(m),b(m)
(Điều kiện: a>0; b>0)
Tỉ số giữa chiều rộng và chiều dài là 5:7 nên \(\dfrac{a}{5}=\dfrac{b}{7}\)
Nửa chu vi vườn hoa là 120:2=60(m)
=>a+b=60
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{5}=\dfrac{b}{7}=\dfrac{a+b}{5+7}=\dfrac{60}{12}=5\)
=>\(\left\{{}\begin{matrix}a=5\cdot5=25\\b=5\cdot7=35\end{matrix}\right.\left(nhận\right)\)
Vậy: Chiều rộng là 25m; chiều dài là 35m

x 2 +2y=xy+x+9 Bước 1: Chuyển tất cả các hằng số và các biểu thức về một vế Chúng ta sẽ đưa tất cả các hạng tử về cùng một vế của phương trình để dễ dàng giải quyết. 𝑥 2 + 2 𝑦 − 𝑥 𝑦 − 𝑥 − 9 = 0 x 2 +2y−xy−x−9=0 Bước 2: Nhóm các hạng tử có 𝑥 x và 𝑦 y lại với nhau Ta nhóm lại theo cách sau: 𝑥 2 − 𝑥 𝑦 − 𝑥 + 2 𝑦 − 9 = 0 x 2 −xy−x+2y−9=0 Bước 3: Thử các giá trị của 𝑥 x và 𝑦 y (vì bài toán yêu cầu tìm số nguyên) Bây giờ, ta thử các giá trị của 𝑥 x và 𝑦 y để tìm nghiệm nguyên. Khi 𝑥 = 3 x=3: Ta thay vào phương trình: 3 2 + 2 𝑦 = 3 𝑦 + 3 + 9 3 2 +2y=3y+3+9 9 + 2 𝑦 = 3 𝑦 + 12 9+2y=3y+12 9 = 𝑦 + 12 9=y+12 𝑦 = − 3 y=−3 Vậy ( 𝑥 , 𝑦 ) = ( 3 , − 3 ) (x,y)=(3,−3) là một nghiệm. Bước 4: Kiểm tra nghiệm Ta kiểm tra lại với 𝑥 = 3 x=3 và 𝑦 = − 3 y=−3 trong phương trình ban đầu: 𝑥 2 + 2 𝑦 = 𝑥 𝑦 + 𝑥 + 9 x 2 +2y=xy+x+9 3 2 + 2 ( − 3 ) = 3 ( − 3 ) + 3 + 9 3 2 +2(−3)=3(−3)+3+9 9 − 6 = − 9 + 3 + 9 9−6=−9+3+9 3 = 3 3=3 Vậy nghiệm ( 3 , − 3 ) (3,−3) đúng. Kết luận: Nghiệm nguyên của phương trình là 𝑥 = 3 x=3 và 𝑦 = − 3 y=−3.

`A = 11/4 - 3/4 : -6/2`
`=> A = 11/4 -3/4 xx -2/6`
`=> A = 11/4 + 1/4`
`=> A=12/4 = 3`
Vậy `A = 3`

Giải:
A = \(\frac12+\frac{1}{2^2}+\frac{1}{2^3}+\cdots+\frac{1}{2^{2024}}\) + \(\frac{1}{2^{2025}}\)
2A = 1 + \(\frac12\) + \(\frac{1}{2^2}\) +......+ \(\frac{1}{2^{2023}}+\frac{1}{2^{2024}}\)
2A - A = 1 + \(\frac12\) + \(\frac{1}{2^2}\) +..+ \(^{}\frac{1}{2^{2024}}\) - ( \(\frac12+\frac{1}{2^2}+\cdots+\frac{1}{2^{2024}}\) + \(\frac{1}{2^{2025}})\)
A = 1 + \(\frac12\) + \(\frac{1}{2^2}\) + ...+ \(\frac{1}{2^{2024}}\) - \(\frac12\) - \(\frac{1}{2^2}\) -...- \(\frac{1}{2^{2024}}\) - \(\frac{1}{2^{^{2025}}}\)
A = (1 - \(\frac{1}{2^{2025}}\)) + (\(\frac12-\frac12\)) + (\(\frac{1}{2^2}\) - \(\frac{1}{2^2}\)) + ...+ (\(\frac{1}{2^{2024}}\) - \(\frac{1}{2^{2024}}\))
A = 1 - \(\frac{1}{2^{2025}}\) + 0 + 0 +0 + ..+ 0
A = 1 - \(\frac{1}{2^{2025}}\) < 1
Vậy A < 1 (đpcm)
