Giải phương trình nghiệm nguyên \(y^3-2x-2=x\left(x+1\right)^2\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a : 3 dư 1 \(\Rightarrow a-1⋮3\)
b : 3 sư 2 \(\Rightarrow b-2⋮3\)
\(\Rightarrow\left(a-1\right)\left(b-2\right)=ab-\left(2a+b\right)+2⋮3\)
Ta có \(a-1⋮3\Rightarrow2a-2⋮3\)
\(\Rightarrow2a-2+b-2=2a+b-4=2a+b-1-3⋮3\Rightarrow2a+b-1⋮3\)
Từ \(ab-\left(2a+b\right)+2=ab-\left(2a+b-1\right)+1⋮3\)
Mà \(2a+b-1⋮3\Rightarrow ab+1⋮3\) => ab : 3 dư 2

\(\left(6-x\right)^2=x-6\)\(< =>\left(6-x\right)^2+6-x=0\)
\(< =>\left(6-x\right)\left(6-x+1\right)=0\)
\(< =>\orbr{\begin{cases}x=6\\x=7\end{cases}}\)
Trả lời:
\(x-6=\left(6-x\right)^2\)
\(\Leftrightarrow\left(x-6\right)-\left(6-x\right)^2=0\)
\(\Leftrightarrow\left(x-6\right)-\left(x-6\right)^2=0\)
\(\Leftrightarrow\left(x-6\right)\left(1-x+6\right)=0\)
\(\Leftrightarrow\left(x-6\right)\left(7-x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-6=0\\7-x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=6\\x=7\end{cases}}}\)
Vậy x = 6; x = 7 là nghiệm của pt.

Trả lời:
Ta có: \(A=\left(x^2+x\right)^2+5y\left(x^2+x\right)+6y^2\)
\(=\left(x^2+x\right)^2+2y\left(x^2+x\right)+3y\left(x^2+x\right)+6y^2\)
\(=\left[\left(x^2+x\right)^2+2y\left(x^2+x\right)\right]+\left[3y\left(x^2+x\right)+6y^2\right]\)
\(=\left(x^2+x\right)\left(x^2+x+2y\right)+3y\left(x^2+x+2y\right)\)
\(=\left(x^2+x+2y\right)\left(x^2+x+3y\right)\)

Trả lời:
+) \(x^4+3x^3-9x-9\)
\(=\left(x^4-9\right)+\left(3x^3-9x\right)\)
\(=\left(x^2-3\right)\left(x^2+3\right)+3x\left(x^2-3\right)\)
\(=\left(x^2-3\right)\left(x^2+3+3x\right)\)
+) \(x^4+3x^3-9x-27\)
\(=\left(x^4+3x^3\right)-\left(9x+27\right)\)
\(=x^3\left(x+3\right)-9\left(x+3\right)\)
\(=\left(x+3\right)\left(x^3-9\right)\)

Bài 1.
a) \(2x^2-2xy-3x+3y=2x\left(x-y\right)-3\left(x-y\right)=\left(2x-3\right)\left(x-y\right)\)
b) \(-x^2-y^2+2xy+16==16-\left(x^2+y^2-2xy\right)=4^2-\left(x-y\right)^2=\left(4-x+y\right)\left(4+x-y\right)\)
c) \(y^2-x^2+2yz+z^2=y^2+2yz+z^2-x^2=\left(y+z\right)^2-x^2=\left(y+z-x\right)\left(y+z+x\right)\)
d) \(3x^2-6xy+3y^2-12z^2=3\left(x^2-2xy+y^2-4z^2\right)=3\left[\left(x-y\right)^2-\left(2z\right)^2\right]\)
\(=3\left(x-y-2z\right)\left(x-y+2z\right)\)
Trả lời:
a, \(2x^2-2xy-3x+3y\)
\(=\left(2x^2-2xy\right)-\left(3x-3y\right)\)
\(=2x\left(x-y\right)-3\left(x-y\right)\)
\(=\left(x-y\right)\left(2x-3\right)\)
b, \(-x^2-y^2+2xy+16\)
\(=16-\left(x^2-2xy+y^2\right)\)
\(=4^2-\left(x-y\right)^2\)
\(=\left(4-x+y\right)\left(4+x-y\right)\)
c, \(y^2-x^2+2yz+z^2\)
\(=\)\(\left(y^2+2yz+z^2\right)-x^2\)
\(=\left(y+z\right)^2-x^2\)
\(=\left(y+z-x\right)\left(y+z+x\right)\)
d, \(3x^2-6xy+3y^2-12z^2\)
\(=3\left(x^2-2xy+y^2-4z^2\right)\)
\(=3\left[\left(x^2-2xy+y^2\right)-4z^2\right]\)
\(=3\left[\left(x-y\right)^2-\left(2z\right)^2\right]\)
\(=3\left(x-y-2z\right)\left(x-y+2z\right)\)

ta có :
\(x^4-1-\left(2x^3-2x\right)=\left(x^2-1\right)\left(x^2-2x+1\right)\)
Vậy \(x^4-1-\left(2x^3-2x\right):\left(x^2-1\right)=x^2-2x+1\)

x2 + 6x - y2 + 9 =
= ( x2 + 6x + 9 ) - y2
= ( x + 3 )2 - y2
= ( x + 3 - y ) . ( x + 3 + y )
Hok tốt!!!!!!!!!!!

ta có
a.\(N=\left(10x\right)^2-2.\left(10x\right)+1=\left(10x-1\right)^2=\left(3-1\right)^2=4\text{ khi }x=\frac{3}{10}\)
b.\(P=\left(5x\right)^2-2.5xy^2+y^4=\left(5x-y^2\right)^2=\left(5.5-4^2\right)=9^2=81\)

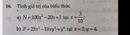
CON KHONG BIET CO OI