Cho f(x)=ax^2+bx+c với a, b, c là các số hữu tỉ. Chứng minh rằng f(-2).f(3) lớn hơn hoặc bằng 0 . Biết 13a+b+2c
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c: \(A=\left|-x+\dfrac{1}{7}\right|+\left|-x-\dfrac{3}{5}\right|-\dfrac{2}{6}\)
\(=\left|x-\dfrac{1}{7}\right|+\left|x+\dfrac{3}{5}\right|-\dfrac{1}{3}\)
\(-\dfrac{3}{5}< x< \dfrac{1}{7}\)
=>\(x+\dfrac{3}{5}>0;x-\dfrac{1}{7}< 0\)
=>\(A=\dfrac{1}{7}-x+x+\dfrac{3}{5}-\dfrac{1}{3}=\dfrac{1}{7}+\dfrac{3}{5}-\dfrac{1}{3}=\dfrac{43}{105}\)
d: \(A=\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|+8\dfrac{1}{5}\)
\(=\left|x-2\dfrac{1}{5}\right|+\left|x-\dfrac{1}{5}\right|+\dfrac{41}{5}\)
\(\dfrac{1}{5}< =x< =2\dfrac{1}{5}\)
=>\(x-\dfrac{1}{5}>=0;x-2\dfrac{1}{5}< =0\)
=>\(D=2\dfrac{1}{5}-x+x-\dfrac{1}{5}+\dfrac{41}{5}=2+\dfrac{41}{5}=\dfrac{51}{5}\)

1: \(\left|x-3,5\right|>=0\forall x\)
\(\left|4,5-y\right|>=0\forall y\)
Do đó: \(\left|x-3,5\right|+\left|4.5-y\right|>=0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-3,5=0\\4,5-y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3,5\\y=4,5\end{matrix}\right.\)
2: \(\left\{{}\begin{matrix}\left|x+\dfrac{2}{3}\right|>=0\forall x\\\left|y-\dfrac{3}{4}\right|>=0\forall y\\\left|z-5\right|>=0\forall z\end{matrix}\right.\)
Do đó: \(\left|x+\dfrac{2}{3}\right|+\left|y-\dfrac{3}{4}\right|+\left|z-5\right|>=0\forall x,y,z\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x+\dfrac{2}{3}=0\\y-\dfrac{3}{4}=0\\z-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{2}{3}\\y=\dfrac{3}{4}\\z=5\end{matrix}\right.\)
3: \(\left|x-2\right|+\left|3-x\right|=0\)
=>|x-2|+|x-3|=0(1)
TH1: x<2
Phương trình (1) sẽ trở thành 2-x+3-x=0
=>5-2x=0
=>2x=5
=>x=2,5(loại)
TH2: 2<=x<3
Phương trình (1) sẽ trở thành x-2+3-x=0
=>1=0(loại)
TH3: x>=3
Phương trình (1) sẽ trở thành x-2+x-3=0
=>2x=5
=>x=2,5(loại)
Vậy: Phương trình vô nghiệm
4: \(\left\{{}\begin{matrix}\left|x-\dfrac{2}{3}\right|>=0\forall x\\\left|x+y+\dfrac{3}{4}\right|>=0\forall x,y\\\left|y-z-\dfrac{5}{6}\right|>=0\forall y,z\end{matrix}\right.\)
Do đó: \(\left|x-\dfrac{2}{3}\right|+\left|x+y+\dfrac{3}{4}\right|+\left|y-z-\dfrac{5}{6}\right|>=0\forall x,y,z\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-\dfrac{2}{3}=0\\x+y+\dfrac{3}{4}=0\\y-z-\dfrac{5}{6}=0\end{matrix}\right.\)
=>\(\begin{matrix}x=\dfrac{2}{3}\\y=-x-\dfrac{3}{4}=-\dfrac{2}{3}-\dfrac{3}{4}=\dfrac{-17}{12}\\z=y-\dfrac{5}{6}=-\dfrac{17}{12}-\dfrac{5}{6}=-\dfrac{27}{12}=-\dfrac{9}{4}\end{matrix}\)
5: \(\left\{{}\begin{matrix}\left|x-\dfrac{2}{3}\right|>=0\forall x\\\left|xy-\dfrac{5}{8}\right|>=0\forall x,y\\\left|yz+\dfrac{3}{4}\right|>=0\forall y,z\end{matrix}\right.\)
Do đó: \(\left|x-\dfrac{2}{3}\right|+\left|xy-\dfrac{5}{8}\right|+\left|yz+\dfrac{3}{4}\right|>=0\forall x,y,z\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-\dfrac{2}{3}=0\\xy-\dfrac{5}{8}=0\\yz+\dfrac{3}{4}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\xy=\dfrac{5}{8}\\yz=-\dfrac{3}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{5}{8}:x=\dfrac{5}{8}:\dfrac{2}{3}=\dfrac{5}{8}\cdot\dfrac{3}{2}=\dfrac{15}{16}\\z=-\dfrac{3}{4}:\dfrac{15}{16}=-\dfrac{3}{4}\cdot\dfrac{16}{15}=\dfrac{-48}{60}=-\dfrac{4}{5}\end{matrix}\right.\)
6: \(\left\{{}\begin{matrix}\left|xy+\dfrac{2}{3}\right|>=0\forall x,y\\\left|yz-\dfrac{8}{9}\right|>=0\forall y,z\\\left|xz+\dfrac{3}{4}\right|>=0\forall x,z\end{matrix}\right.\)
Do đó: \(\left|xy+\dfrac{2}{3}\right|+\left|yz-\dfrac{8}{9}\right|+\left|xz+\dfrac{3}{4}\right|>=0\forall x,y,z\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}xy+\dfrac{2}{3}=0\\yz-\dfrac{8}{9}=0\\xz+\dfrac{3}{4}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}xy=-\dfrac{2}{3}\\yz=\dfrac{8}{9}\\xz=-\dfrac{3}{4}\end{matrix}\right.\)
=>\(\left(xyz\right)^2=-\dfrac{2}{3}\cdot\dfrac{8}{9}\cdot\dfrac{-3}{4}=\dfrac{1}{2}\cdot\dfrac{8}{9}=\dfrac{4}{9}\)
=>\(\left[{}\begin{matrix}xyz=\dfrac{2}{3}\\xyz=-\dfrac{2}{3}\end{matrix}\right.\)
TH1: xyz=2/3
=>\(\left\{{}\begin{matrix}z=\dfrac{xyz}{xy}=\dfrac{2}{3}:\dfrac{-2}{3}=-1\\x=\dfrac{xyz}{yz}=\dfrac{2}{3}:\dfrac{8}{9}=\dfrac{2}{3}\cdot\dfrac{9}{8}=\dfrac{18}{24}=\dfrac{3}{4}\\y=\dfrac{xyz}{xz}=\dfrac{2}{3}:\dfrac{-3}{4}=\dfrac{2}{3}\cdot\dfrac{4}{-3}=-\dfrac{8}{9}\end{matrix}\right.\)
TH2: xyz=-2/3
=>\(\left\{{}\begin{matrix}z=\dfrac{xyz}{xy}=-\dfrac{2}{3}:\dfrac{-2}{3}=1\\x=\dfrac{xyz}{yz}=-\dfrac{2}{3}:\dfrac{8}{9}=\dfrac{-2}{3}\cdot\dfrac{9}{8}=\dfrac{-18}{24}=\dfrac{-3}{4}\\y=\dfrac{xyz}{xz}=\dfrac{-2}{3}:\dfrac{-3}{4}=\dfrac{-2}{3}\cdot\dfrac{4}{-3}=\dfrac{8}{9}\end{matrix}\right.\)

| GT | ΔABC vuông tại A \(E\in BC;F\in BA\) BE=BA; BF=BC BD là phân giác của góc ABC; \(D\in AC\) |
| KL | a: ΔABD=ΔEBD DA=DE b: BD là đường trung trực của AE AD<DC c: E,D,F thẳng hàng |
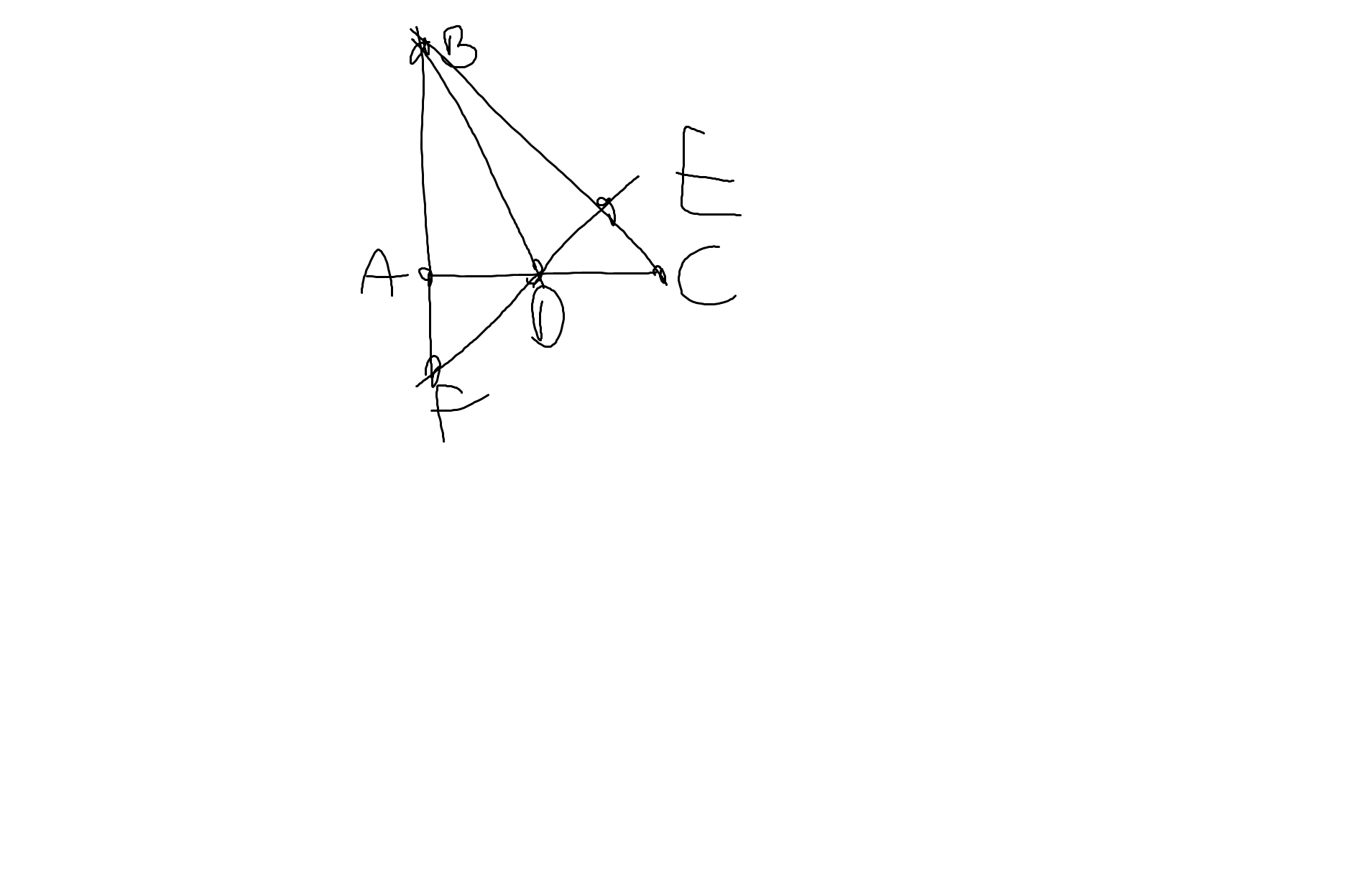
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
=>DA=DE
b: Ta có: BA=BE
=>B nằm trên đường trung trực của AE(1)
Ta có: DA=DE
=>D nằm trên đường trung trực của AE(2)
Từ (1),(2) suy ra BD là đường trung trực của AE
ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
=>\(\widehat{BED}=90^0\)
=>DE\(\perp\)BC tại E
Ta có: ΔDEC vuông tại E
=>DC>DE
mà DE=DA
nên DC>DA
=>AD<DC
c: Ta có: BA+AF=BF
BE+EC=BC
mà BA=BE và BF=BC
nên AF=EC
Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
AF=EC
Do đó: ΔDAF=ΔDEC
=>\(\widehat{ADF}=\widehat{EDC}\)
=>\(\widehat{ADF}+\widehat{ADE}=180^0\)
=>F,D,E thẳng hàng

a: Các biến cố không thể là C
Biến cố chắc chắn là D
b: Biến cố ngẫu nhiên là A,B
A: "Mai lấy được bút màu đỏ"
n(A)=1
\(P_A=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{1}{3}\)
B: "Mai lấy được bút màu xanh"
=>n(B)=2
=>\(P_B=\dfrac{n\left(B\right)}{n\left(\Omega\right)}=\dfrac{2}{3}\)
tk ạ
a) Biến cố không thể là C: "Mai lấy được chiếc bút màu đen", vì trong hộp chỉ có hai chiếc bút màu xanh và một chiếc bút màu đỏ.
Biến cố chắc chắn là "Mai lấy được chiếc bút màu đỏ hoặc màu xanh", vì không có trường hợp nào khác xảy ra.
b) Xác suất của các biến cố:
P(A) = 1/3 (vì trong hộp có một chiếc bút màu đỏ và hai chiếc bút màu xanh)
P(B) = 2/3
P(C) = 0
P(A ∪ B) = P(A) + P(B) - P(A ∩ B) = 1/3 + 2/3 - 0 = 1
Chú ý rằng P(A ∪ B) là biến cố "Mai lấy được chiếc bút màu đỏ hoặc màu xanh", và P(A ∩ B) = 0 vì không thể lấy được cả hai chiếc bút cùng lúc.

\(B=\left(\dfrac{1}{2^2}-1\right)\cdot\left(\dfrac{1}{3^2}-1\right)\cdot...\cdot\left(\dfrac{1}{1000^2}-1\right)\)
\(=\left(\dfrac{1}{2}-1\right)\cdot\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{1000}-1\right)\cdot\left(\dfrac{1}{2}+1\right)\cdot\left(\dfrac{1}{3}+1\right)\cdot...\cdot\left(\dfrac{1}{1000}+1\right)\)
\(=\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\cdot\dfrac{-999}{1000}\cdot\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot....\cdot\dfrac{1001}{1000}\)
\(=\dfrac{-1}{1000}\cdot\dfrac{1001}{2}=\dfrac{-1001}{2000}\)

Bài 3:
a: \(3\in N;3\in Z;3\in Q\)
b: \(10\in N;10\in Z;10\in Q\)
c: \(-\dfrac{3}{7}\in Q\)
d: \(-2\in Z;-2\in Q\)
Bài 2:
\(\dfrac{-3}{5}=\dfrac{-27}{45};\dfrac{-5}{9}=\dfrac{-25}{45};-1\dfrac{2}{3}=\dfrac{-5}{3}=\dfrac{-75}{45};0,5=\dfrac{22,5}{45};\dfrac{10}{9}=\dfrac{50}{45}\)
mà -75<-27<-25<22,5<50
nên \(-1\dfrac{2}{3}< -\dfrac{3}{5}< -\dfrac{5}{9}< \dfrac{1}{2}< \dfrac{10}{9}\)
Bài 1:
a: \(\dfrac{9}{70}=\dfrac{9\cdot3}{70\cdot3}=\dfrac{27}{210};\dfrac{5}{42}=\dfrac{5\cdot5}{42\cdot5}=\dfrac{25}{210}\)
mà 27>25
nên \(\dfrac{9}{70}>\dfrac{5}{42}\)
b: \(\dfrac{-4}{27}=\dfrac{-4\cdot7}{27\cdot7}=\dfrac{-28}{189};\dfrac{10}{-63}=\dfrac{-10}{63}=\dfrac{-10\cdot3}{63\cdot3}=\dfrac{-30}{189}\)
mà -28>-30
nên \(\dfrac{-4}{27}>\dfrac{10}{-63}\)
c: \(\dfrac{999}{556}=1+\dfrac{443}{556};\dfrac{1000}{557}=1+\dfrac{443}{557}\)
mà \(\dfrac{443}{556}>\dfrac{443}{557}\)
nên \(\dfrac{999}{556}>\dfrac{1000}{557}\)
d: \(\dfrac{-2}{15}< 0;\dfrac{-10}{-11}=\dfrac{10}{11}>0\)
Do đó: \(\dfrac{-2}{15}< \dfrac{-10}{-11}\)

a: Xét ΔAMC và ΔDMB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔAMC=ΔDMB
b: ΔAMC=ΔDMB
=>\(\widehat{MAC}=\widehat{MDB}\)
=>AC//DB
mà AC\(\perp\)AB
nên BD\(\perp\)BA
c: Xét ΔCAB vuông tại A và ΔDBA vuông tại B có
BA chung
AC=BD
Do đó: ΔCAB=ΔDBA
=>CB=DA
mà \(AM=\dfrac{1}{2}AD\)
nên \(AM=\dfrac{1}{2}CB\)

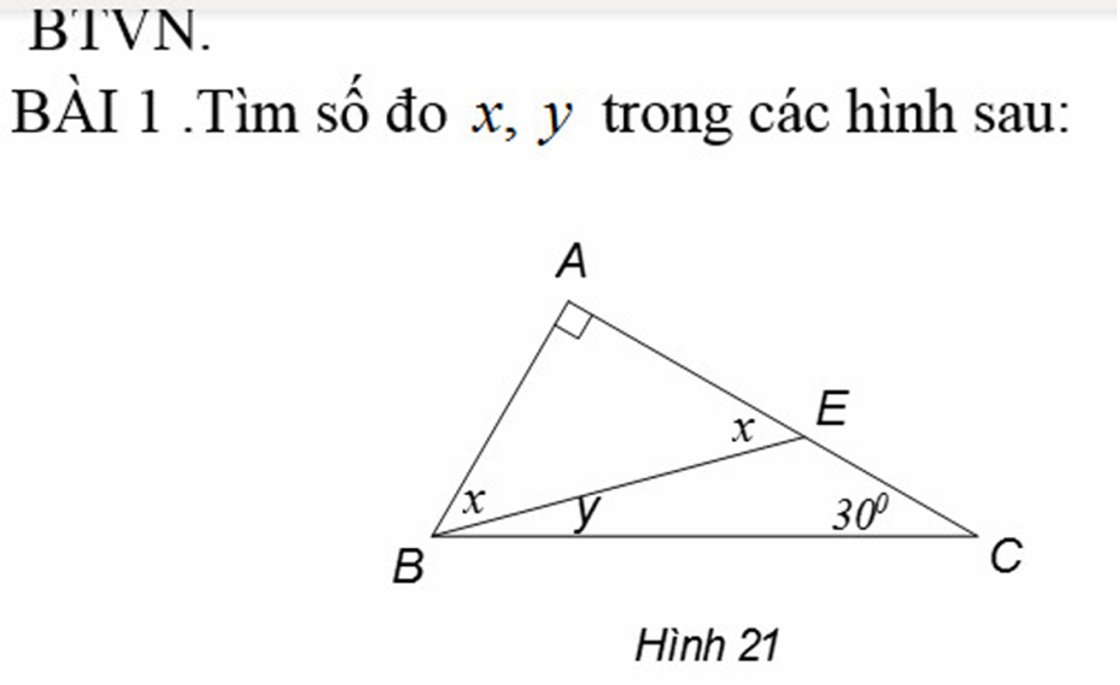
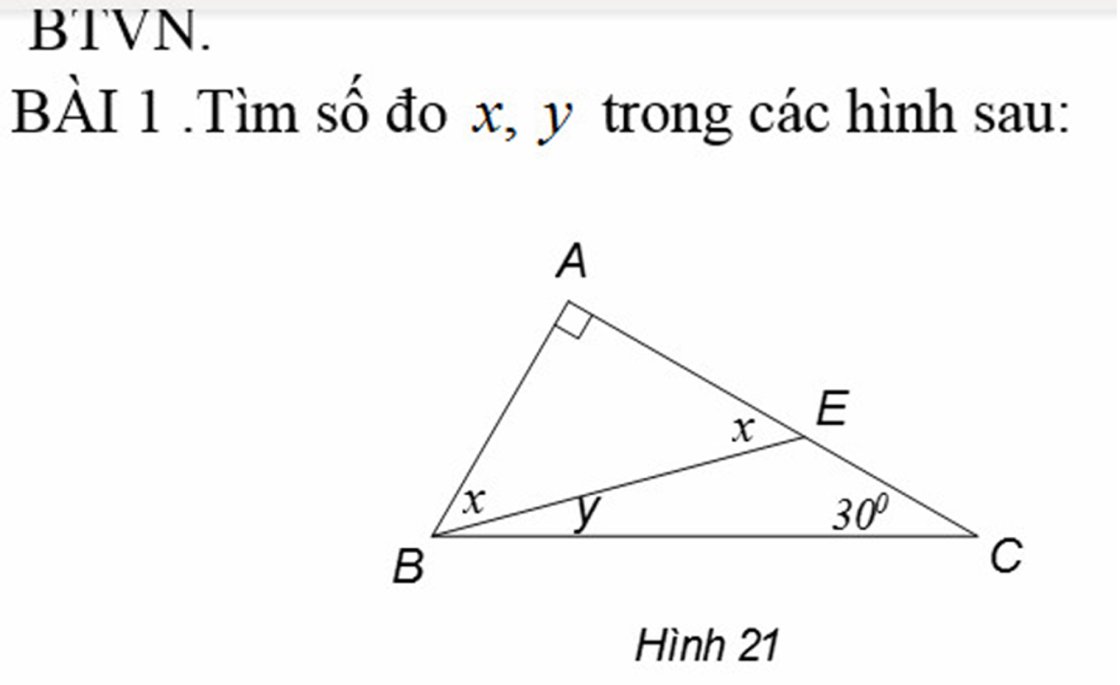
Xét ΔABE có: \(\widehat{BAE}+\widehat{ABE}+\widehat{AEB}=180^o\)
\(\Rightarrow90^o+x+x=180^o\Rightarrow2x=180^o-90^o=90^o\)
\(\Rightarrow x=\dfrac{90^o}{2}=45^o\)
Xét ΔABC có: \(\widehat{ABC}+\widehat{BAC}+\widehat{CAB}=180^o\)
\(\Rightarrow\left(x+y\right)+90^o+30^o=180^o\)
\(\Rightarrow\left(x+y\right)+120^o=180^o\)
\(\Rightarrow45^o+y=180^o-120^o\)
\(\Rightarrow45^o+y=60^o\)
\(\Rightarrow y=60^o-45^o=15^o\)
∆ABE vuông tại A (gt)
⇒ ∠ABE + ∠AEB = 90⁰
⇒ x + x = 90⁰
⇒ x = 90⁰ : 2
= 45⁰
∆ABC vuông tại A (gt)
⇒ ∠ABC + ∠ACB = 90⁰
⇒ ∠ABC = 90⁰ - ∠ACB
= 90⁰ - 30⁰
= 60⁰
⇒ y = ∠ABC - x
= 60⁰ - 45⁰
= 15⁰
 cú ét ô ét
cú ét ô ét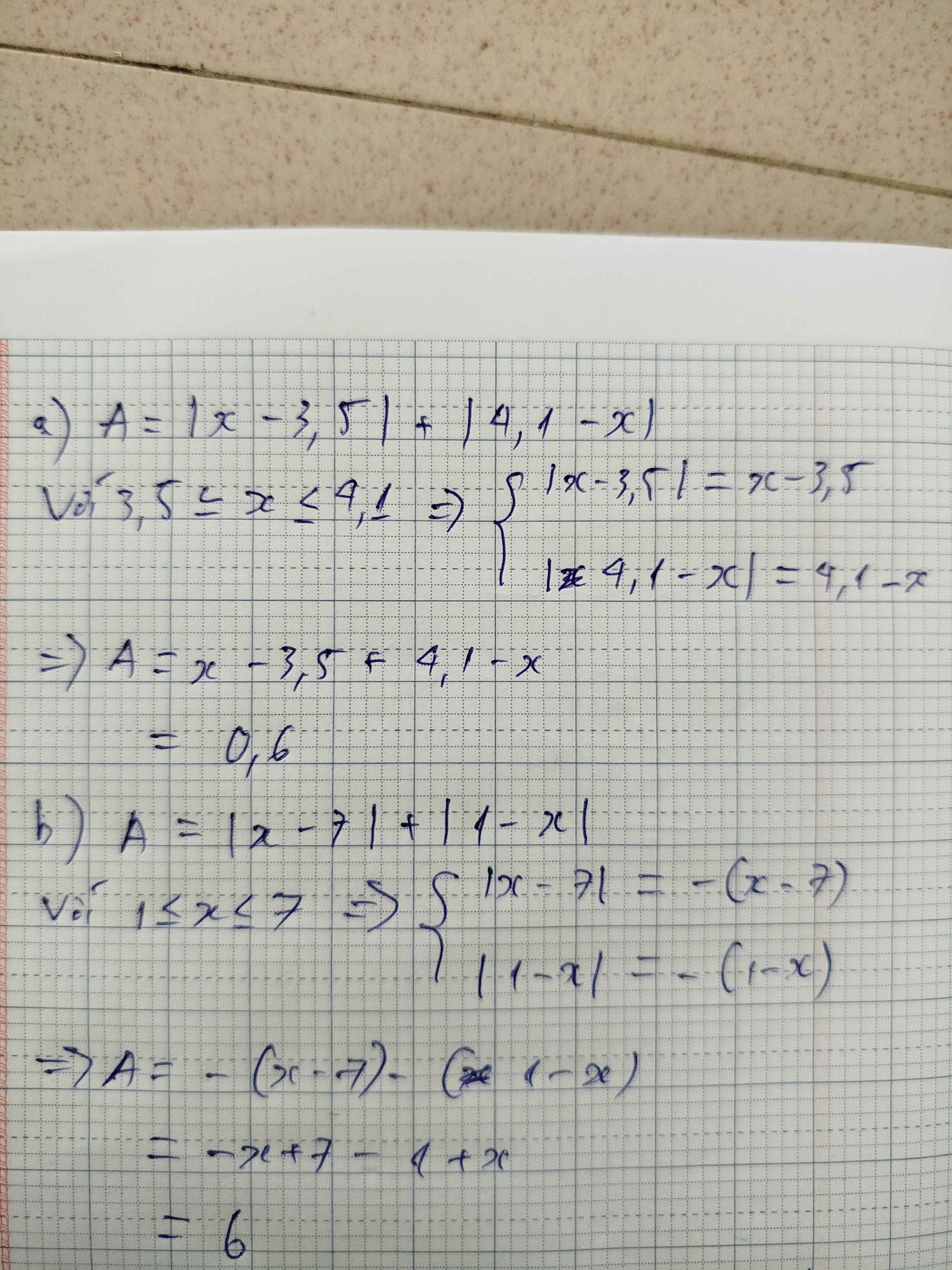


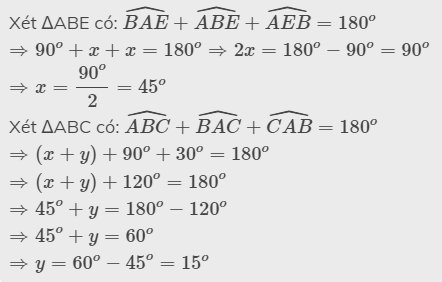
Biết $13a+b+2c$ như thế nào hả bạn?