Tìm Min của Q=\(\frac{x+3z}{y+x}+\frac{z+3x}{y+z}+\frac{4y}{x+z}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


) Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC.
b) Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên:
c) ΔOIO' vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
IA2 = AO.AO' = 9.4 = 36
=> IA = 6 (cm)
Vậy BC = 2.IA = 2.6 = 12 (cm)
A B C O' O I 4 9
Bài làm
a) Ta thấy: BC là tiếp tuyến chung ngoài và tiếp tuyến chung trong của hai đường tròn (O') và (O) cắt nhau tại I
=> CI = IA = IB (theo tính chất hai tiếp tuyến cắt nhau)
Xét tam giác ABC có: IA = 1/2BC
=> Tam giác ABC vuông tại A
Do đó: góc BAC = 90o (đpcm)
b) Ta thấy: O'I là tia phân giác của CO'O (theo tính chất hai tiếp tuyến cắt nhau)
=> \(\widehat{IO'O}=\frac{1}{2}\widehat{CO'O}\Rightarrow2\widehat{IO'O}=\widehat{CO'O}\)
Ta lại thấy: OI là tia phân giác của BOO' (theo tính chất hai tiếp tuyến cắt nhau)
=> \(\widehat{IOO'}=\frac{1}{2}\widehat{BOO'}\Rightarrow2\widehat{IOO'}=\widehat{BOO'}\)
Xét tứ giác O'CBO có:
\(\widehat{O'CB}+\widehat{CBO}+\widehat{B\text{OO}'}+\widehat{\text{OO}'C}=360^0\)(tổng 4 góc của tứ giác)
Hay \(90^0+90^0+2\widehat{IO'O}+2\widehat{IOO'}=360^0\)
=> \(2\left(\widehat{IO'O}+\widehat{IOO'}\right)=360^0-90^0-90^0=180^0\)
=> \(\widehat{IO'O}+\widehat{IOO'}=\frac{180^0}{2}=90^0\)\
Xét tam giác O'IO có:
\(\widehat{IO'O}+\widehat{IOO'}+\widehat{O'IO}=180^0\)(Tổng ba góc trong tam giác)
Hay \(90^0+\widehat{\text{OIO}'}=180^0\)
=> \(\widehat{\text{OIO}'}=180^0-90^0=90^0\)
Vậy góc OIO' = 90o
c) Xét tam giác O'IO vuông tại I có:
Đường cao IA
Theo hệ thức lượng trong tam giác:
Ta có: IA2 = OA * O'A
hay IA2 = 4 * 9
=> IA = 6 (cm)
Mà IA = IC = IB = 6 (cm)
=> IC + IB = BC
hay BC = 6 + 6 = 12 (cm)
Vậy BC = 12cm

a) Tâm của các đường tròn có bán kính 1cm tiếp xúc ngoài với đường tròn (O; 3cm) nằm trên đường tròn (O; 4cm).
b) Tâm của các đường tròn có bán kính 1cm tiếp xúc trong với đường tròn (O; 3cm) năm trên đường tròn (O; 2cm).
a) Tâm của các đường tròn có bán kính 1cm tiếp xúc ngoài với đường tròn (O; 3cm) nằm trên đường tròn (O; 4cm).
b) Tâm của các đường tròn có bán kính 1cm tiếp xúc trong với đường tròn (O; 3cm) năm trên đường tròn (O; 2cm).

Vẽ OM⊥AB⇒OM⊥CD.
Xét đường tròn (O;OC) (đường tròn nhỏ) có OM là một phần đường kính, CD là dây và OM⊥CD nên M là trung điểm của CD hay MC=MD (định lý)
Xét đường tròn (O;OA) (đường tròn lớn) có OM là một phần đường kính, AB là dây và OM⊥AB nên M là trung điểm của AB hay MA=MB (định lý)
Ta có MA=MB và MC=MD (cmt) nên trừ các đoạn thẳng theo vế với vế ta được MA−MC=MB−MD ⇒AC=BD.
Nhận xét. Kết luận bài toán vẫn được giữ nguyên nếu C và D đổi chỗ cho nhau.

Vẽ OM⊥AB⇒OM⊥CD.
Xét đường tròn (O;OC) (đường tròn nhỏ) có OM là một phần đường kính, CD là dây và OM⊥CD nên M là trung điểm của CD hay MC=MD (định lý)
Xét đường tròn (O;OA) (đường tròn lớn) có OM là một phần đường kính, AB là dây và OM⊥AB nên M là trung điểm của AB hay MA=MB (định lý)
Ta có MA=MB và MC=MD (cmt) nên trừ các đoạn thẳng theo vế với vế ta được MA−MC=MB−MD ⇒AC=BD.
Nhận xét. Kết luận bài toán vẫn được giữ nguyên nếu C và D đổi chỗ cho nhau.
á em lộn
a) Cho hai đường tròn (O; R)(O; R) và (O′; r)(O′; r) với R>r. Nếu OO′=R−rOO′=R−r thì hai đường tròn tiếp xúc trong.
b) +) Nếu tam giác có ba đỉnh nằm trên đường tròn và có 1 cạnh là đường kính của đường tròn đó thì tam giác đó là tam giác vuông.
+) Trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây đó.

Câu 5c) Phương trình hoành độ giao điểm \(\left(P\right)\)và \(\left(d\right)\)là:
\(\frac{1}{2}x^2=2x+m\Leftrightarrow x^2-4x-2m=0\)(*)
Để \(\left(P\right)\)và \(\left(d\right)\)cắt nhau tại hai điểm phân biệt thì phương trình (*) có hai nghiệm phân biệt suy ra
\(\Delta'=4+2m>0\Leftrightarrow m>-2\).
Theo Viet:
\(\hept{\begin{cases}x_1+x_2=4\\x_1x_2=-2m\end{cases}}\)
\(\left(x_1x_2+1\right)^2=x_1+x_2+x_1x_2+3\)
\(\Leftrightarrow\left(-2m+1\right)^2=4-2m+3\)
\(\Leftrightarrow\orbr{\begin{cases}m=-1\\m=\frac{3}{2}\end{cases}}\)(thỏa mãn)


bài 7 : a ) thay m = 3 vào hàm số y = mx +4 có : y = 3x + 4
pt hoành độ giao đieẻm của 2 đồ thị hafm số y =x2 và y = 3x + 4
x2 = 3x + 4
\(\Leftrightarrow\) x2 - 3x -4 = 0
a - b + c = 1 + 3 - 4 = 0
\(\Rightarrow\)pt có 2 nghiệm x1 = -1 ; x2 = -
thay x = -1 vào hàm số y = x2 có : y = (-1)2 = 1
thay x = 4 vào hàm số y = x2 có : y = 42 = 16
vậy toạ độ giao điểm cần tìm là ( -1 ; 1 ) ; (4 ; 16 )


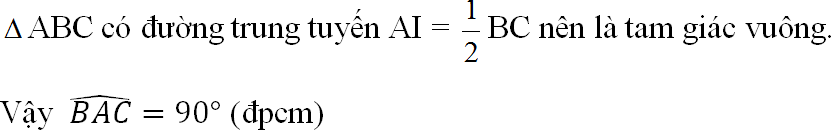
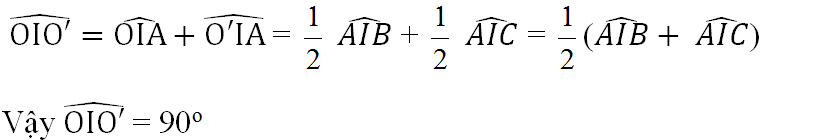
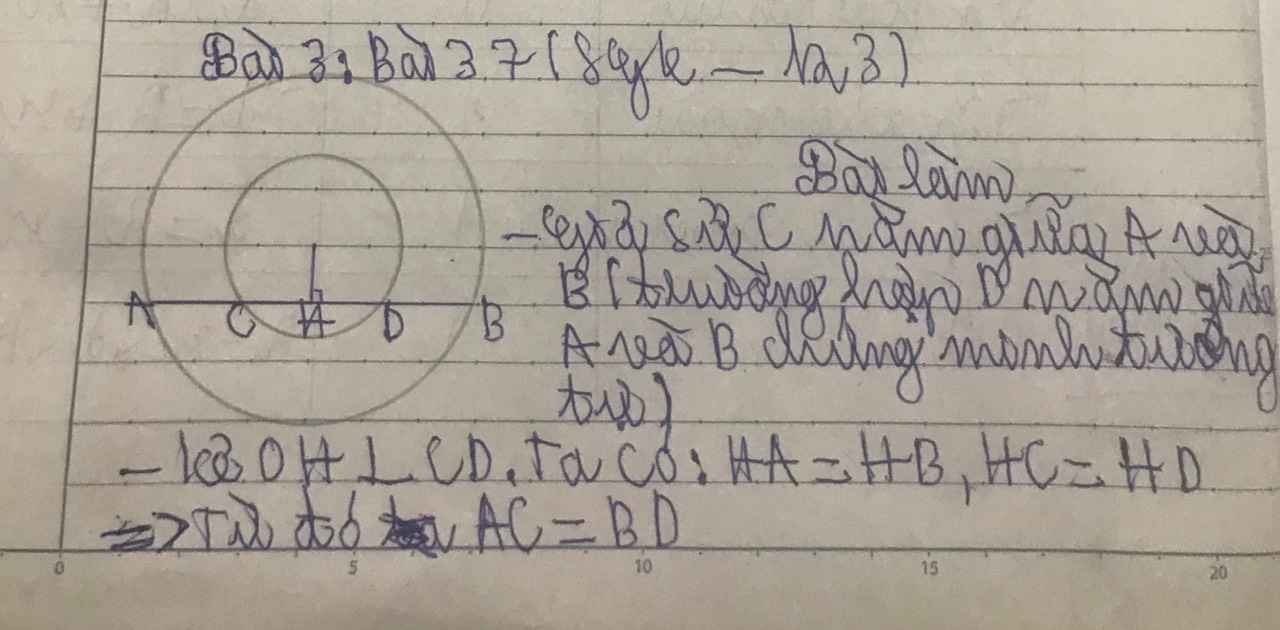





Với x,y,z > 0 có :\(Q=\frac{x+3z}{x+y}+\frac{z+3x}{y+z}+\frac{4y}{x+z}\)
\(=\frac{2z}{x+y}+\frac{2x}{y+z}+\frac{2y}{x+z}+\frac{x+z}{x+y}+\frac{x+z}{y+z}+\frac{2y}{x+z}\)
Đặt P = \(\frac{x+z}{x+y}+\frac{x+z}{y+z}+\frac{2y}{x+z}\)
=> P + 1 = \(\frac{x+z}{x+y}+\frac{x+z}{y+z}+\left(\frac{2y}{x+z}+1\right)\)
= \(\frac{x+z}{x+y}+\frac{x+z}{y+z}+\frac{x+z+2y}{x+z}=\frac{x+z}{x+y}+\frac{x+z}{y+z}+\frac{x+y}{x+z}+\frac{y+z}{x+z}\)
= \(\left(\frac{x+z}{x+y}+\frac{x+y}{x+z}\right)+\left(\frac{x+z}{y+z}+\frac{y+z}{x+z}\right)\ge2+2=4\)
=> P \(\ge\)3 (Dấu "=" xảy ra <=> x = y = z)
Đặt T = \(\frac{2z}{x+y}+\frac{2x}{y+z}+\frac{2y}{x+z}=2\left(\frac{z}{x+y}+\frac{x}{y+z}+\frac{y}{x+z}\right)\)
\(=2\left(\frac{x+y+z}{x+y}+\frac{x+y+z}{y+z}+\frac{x+y+z}{x+z}-3\right)\)
\(=2\left(x+y+z\right)\left(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}\right)-6\)
\(=\left(x+y+y+z+z+x\right)\left(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}\right)-6\)
\(=1+\frac{x+y}{y+z}+\frac{x+y}{z+x}+\frac{y+z}{x+y}+1+\frac{y+z}{z+x}+\frac{z+x}{x+y}+\frac{z+x}{y+z}+1-6\)
\(=\left(\frac{x+y}{y+z}+\frac{y+z}{y+x}\right)+\left(\frac{x+y}{z+x}+\frac{z+x}{x+y}\right)+\left(\frac{z+x}{y+z}+\frac{y+z}{x+z}\right)-3\)
\(\ge2+2+2-3=3\)(Dấu "=" xảy ra <=> x = y = z)
Mà Q = P + T \(\ge\) 3 + 3 = 6
Dấu "=" xảy ra <=> x =y = z
Vậy Min Q = 6 <=> x = y = z