Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
a) Ta có: {∠ABD=∠EBD(do BD là phân giác góc B)∠BAD=∠BED=900{∠ABD=∠EBD(do BD là phân giác góc B)∠BAD=∠BED=900
⇒1800−∠ABD−∠BAD=1800−∠EBD−∠BED⇒1800−∠ABD−∠BAD=1800−∠EBD−∠BED
⇔∠BDA=∠BDE⇔∠BDA=∠BDE
Xét tam giác ABDABD và EBDEBD có:
⎧⎪⎨⎪⎩BD chung∠ABD=∠EBD∠BDA=∠BDE⇒△ABD=△EBD(g.c.g){BD chung∠ABD=∠EBD∠BDA=∠BDE⇒△ABD=△EBD(g.c.g)
Ta có đpcm.
b) Theo phần a △ABD=△EBD⇒BA=BE△ABD=△EBD⇒BA=BE
Do đó tam giác BAEBAE cân tại BB
⇒∠BEA=∠BAE⇒∠BEA=∠BAE
Mà ∠BEA+∠BAE=1800−∠ABE=1800−600=1200∠BEA+∠BAE=1800−∠ABE=1800−600=1200
Suy ra ∠BEA=∠BAE=600=∠ABE∠BEA=∠BAE=600=∠ABE
Do đó tam giác ABEABE đều
c)
Có: cosˆABC=ABBC⇔cos600=5BC⇔12=5BCcosABC^=ABBC⇔cos600=5BC⇔12=5BC
⇔BC=10⇔BC=10 (cm)

`Answer:`
Sửa đề phần c: Chứng minh KF//BC.
C H B A F K
a. Xét `\triangleAHB` và `\triangleAHC`
`AH` chung
`\hat{AHB}=\hat{AHC}=90^o`
`AB=AC`
`=>\triangleAHB=\triangleAHC(ch-cgv)`
b. Xét `\triangleFAH` và `\triangleKAH`
`AH` chung
`\hat{FAH}=\hat{KAH}`
`\hat{AFH}=\hat{AKH}=90^o`
`=>\triangleFAH=\triangleKAH(ch-gn)`
`=>HK=HF`
c. Theo phần b. `\triangleFAH=\triangleKAH`
`=>AF=AK`
`=>\triangleAFK` cân ở `A`
Ta có: `\triangleAFK` cân ở `A` và `\triangleABC` cân ở `A`
`=>\hat{AFK}=\hat{ABC}` mà hai góc này ở vị trí đồng vị \(\Rightarrow KF//BC\)
hình tự vẽ nhé.
xét: \(\Delta AHB\) VÀ \(\Delta AHC\) CÓ:
\(\widehat{ABH}=\widehat{ACH}\)(DO TAM GIÁC ABC CÂN TẠI A)
\(AB=AC\)(DO TAM GIÁC ABC CÂN TẠI A)
\(\widehat{AHB}=\widehat{AHC}=90^0\)
\(\Rightarrow\Delta AHB=\Delta AHC\left(ch-gn\right)\left(1\right)\)
b) TỪ (1)\(\Rightarrow BH=CH\)(2 cạnh tương ứng)
XÉT: \(\Delta KBH\)VÀ \(\Delta FCH\) CÓ:
\(BH=CH\left(cmt\right)\)
\(\widehat{BKH}=\widehat{CFH}=90^0\)
\(\widehat{KBH}=\widehat{FCH}\left(\widehat{B}=\widehat{C}\right)\)
\(\Rightarrow\Delta KBH=\Delta FCH\left(ch-gn\right)\)
\(\Rightarrow HK=HF;BK=FC\)(2 cạnh tương ứng)(đpcm)
c) ta có: \(AB=AC;;BK=FK\left(cmt\right)\)
\(\Rightarrow AB-BK=AC-FC\)
\(\Rightarrow AK=AF\Rightarrow\Delta AKF\) cân tại A
\(\Rightarrow\widehat{AKF}=\frac{180^0-\widehat{A}}{2}\left(2\right)\)
lại có \(\Delta ABC\)cân tại A\(\Rightarrow\widehat{ABC}=\frac{180^0-\widehat{A}}{2}\left(3\right)\)
TỪ (2)VÀ (3)\(\Rightarrow\widehat{AKF}=\widehat{ABC}\left(=\frac{180^0-\widehat{A}}{2}\right)\)
mà 2 góc này ở vị trí đồng vị \(\Rightarrow KF\\ BC\left(đpcm\right)\)

\(|5x-2|=98\)
\(TH1:5x-2>0\Leftrightarrow x>\frac{2}{5}\)Khi đó \(|5x-2|=5x-2\)
Ta có:\(5x-2=98\)
\(\Leftrightarrow5x=100\)
\(\Leftrightarrow x=20\left(TM\right)\)
\(TH2:5x-2< 0\Leftrightarrow x< \frac{2}{5}\)Khi đó:\(5x-2=2-5x\)
Ta có:\(2-5x=98\)
\(\Leftrightarrow5x=-96\)
\(\Leftrightarrow x=-\frac{96}{5}\left(TM\right)\)
Vậy \(x\in\left\{-\frac{96}{5};20\right\}\)
\(|5x-2|=98 \Leftrightarrow\orbr{\begin{cases}5x-2=98\\5x-2=-98\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=20\\x=-19,2\end{cases}}\)

a) Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E ta có:
Chung DB
Góc ABD = Góc EBD ( BD là tia phân giác của góc ABC)
⇒ Tam giác ABD = Tam giac EBD ( cạnh huyền = góc nhọn)
b)Ta có tam giác ABD = tam giác EBD ( theo a)
⇒AB = EB ( 2 cạnh tương ứng)
⇒ Tam giác ABE cân tại B ( Định nghĩa tam giác cân)

a, Xét tam giác ABC cân tại A
có AH là đường cao
đồng thời là đường phân giác, đường trung tuyến
=> HB = HC ; ^BAH = ^CAH
b, Ta có HB = BC/2 = 4 cm
Xét tam giác AHB vuông tại H
\(AH=\sqrt{AB^2-HB^2}=3cm\)
c, Xét tam giác ADH và tam giác AEH
AH _ chung
^DAH = ^EAH (cmt)
Vậy tam giác ADH = tam giác AEH (ch-cgv)
=> DH = EH ( 2 cạnh tương ứng )
Vậy tam giác HDE cân tại H

`Answer:`
Ảnh mờ quá nên mình có làm sai đề thì bạn bảo nhé.
\(A=\frac{10^{2011}+1}{20^{2012}+1}\)
\(\Rightarrow10A=\frac{10^{2012}+10}{10^{2012}+1}=1+\frac{9}{10^{2012}+1}\)
\(B=\frac{10^{2012}+1}{10^{2013}+1}\)
\(\Rightarrow10B=\frac{10^{2013}+10}{10^{2013}+1}=1+\frac{9}{10^{2013}+1}\)
Mà \(10^{2012}+1< 10^{2013}+1\)
\(\Rightarrow\frac{9}{10^{2012}+1}>\frac{9}{10^{2013}+1}\)
\(\Rightarrow1+\frac{9}{10^{2012}+1}>1+\frac{9}{10^{2013}+1}\) hay \(10A>10B\)
Vậy `A>B`
B<102012+1+9102013+1+9=102012+10102013+10=10(102011+1)10(102012+1)=102011+1102012+1=A
Vậy A > B

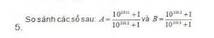
\(-x^4y^2x^2x^2\left(-y\right)^3=x^8y^5\)