một mảnh đất hình thang được vẽ trên bản đồ tỉ lệ 1 chia 1.000 tính diện tích mảnh đất theo đơn vị héc ta
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số thỏa mãn đề bài là \(x\) ( 100 ≤ \(x\) ≤ 999)
⇒ \(x\) ⋮ 56 (1)
⇒ \(x\) ⋮ 7
⇒ \(x\) ⋮ 72 ( một số chính phương chia hết cho một số nguyên tố thì sẽ chia hết cho bình phương của số nguyên tố đó.)
⇒ \(x\) ⋮ 49 (2)
Kết hợp (1) và (2) ta có: \(x\) \(\in\) BC(49; 56)
56 = 7 \(\times\) 23
49 = 72
BCNN(49;56) = 23 \(\times\) 72 = 392
⇒ \(x\) \(\in\) {0; 392; 784; 1176; ....}
784 = 282 < 999 ( thỏa mãn)
182 < 392 < 192 vậy 392 không phải là số chính phương loại
Vậy \(x\) = 784
Kết luận: Số chính phương có 3 chữ số chia hết cho 56 là: 784

Khi ta bớt ở cả hai số đi cùng một số đơn vị thì hiệu của hai số lúc sau không đổi và bằng:
150 - 94 = 56
Theo bài ra ta có sơ đồ:
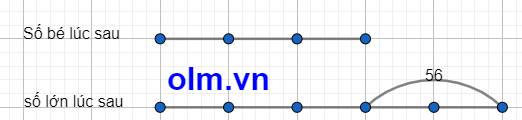
Theo sơ đồ ta có:
Số bé lúc sau là: 56 : ( 5 - 3) \(\times\)3 = 84
Số cần bớt ở cả hai số là: 94 - 84 = 10
Đáp số: 10

Lời giải:
Theo bài ra ta có:
$\frac{94-k}{150-k}=\frac{3}{5}$
$\Rightarrow 5\times (94-k)=3\times (150-k)$
$\Rightarrow 5\times 94-5\times k = 3\times 150-3\times k$
$\Rightarrow 470-5\times k = 450-3\times k$
$\Rightarrow 470-450=5\times k - 3\times k$
$\Rightarrow 20=2\times k$
$\Rightarrow k=20:2=10$

9Đổi 15 phút = 1/4 giờ=0,25 giờ
Sau 15 phút xe đạp đã đi được số km là:
22 x 0,25 = 5,5 ( km )
Xe đạp còn phải đi số km nữa là:
299,5 - 5,5 = 294 ( km )
Hiệu vận tốc 2 xe là:
62 - 22 = 40 ( km/giờ )
Sau số thời gian thì 2 xe gặp nhau là:
294 : 40 = 7,35 ( giờ )
Đổi 7,35 giờ = 7 giờ 21 phút
Đáp số :7 giờ 21 phút
NHỚ TICK NHA


Lời giải:
Đặt $x-y=a; y-z=b, z-x=c$
$\Rightarrow a+b+c=0$
Theo đề ta có:
$(x-y)^2+(y-z)^2+(z-x)^2=[(z-x)-(x-y)]^2+[(x-y)-(y-z)]^2+[(y-z)-(z-x)]^2$
$\Leftrightarrow a^2+b^2+c^2=(c-a)^2+(a-b)^2+(b-c)^2$
$\Leftrightarrow a^2+b^2+c^2=2a^2+2b^2+2c^2-2(ab+bc+ac)$
$\Leftrightarrow 2(a^2+b^2+c^2)=a^2+b^2+c^2+2(ab+bc+ac)$
$\Leftrightarrow 2(a^2+b^2+c^2)=(a+b+c)^2=0$
$\Rightarrow a^2+b^2+c^2=0$
$\Rightarrow a=b=c=0$
$\Leftrightarrow x-y=y-z=z-x=0$
$\Leftrightarrow x=y=z$

Để Olm.vn giúp em nhé
Tính:
A = \(\dfrac{7}{2}\) + \(\dfrac{7}{4}\) + \(\dfrac{7}{8}\) + \(\dfrac{7}{16}\)+...+ \(\dfrac{7}{256}\)
A = \(\dfrac{7}{2}\) + \(\dfrac{7}{4}\) + \(\dfrac{7}{8}\) + \(\dfrac{7}{16}\) +...+ \(\dfrac{7}{128}\)+ \(\dfrac{7}{256}\)
A\(\times\) 2 = 7 + \(\dfrac{7}{2}\) + \(\dfrac{7}{4}\) + \(\dfrac{7}{8}\)+ \(\dfrac{7}{16}\)+...+ \(\dfrac{7}{128}\)
A \(\times\) 2 - A = 7 - \(\dfrac{7}{256}\)
A \(\times\) (2-1) = \(\dfrac{1785}{256}\)
A = \(\dfrac{1785}{256}\)
A =\(\dfrac{7}{2}\)+\(\dfrac{7}{4}\)+\(\dfrac{7}{8}\)+...+\(\dfrac{7}{256}\)
A*2 =7+\(\dfrac{7}{2}\)+\(\dfrac{7}{4}\)+...+\(\dfrac{7}{256}\)
A*2-A=7-\(\dfrac{7}{256}\)
A=\(\dfrac{\text{1785 }}{256}\)

Gọi P là 1 giá trị của biểu thức trên.
Ta có \(P=\dfrac{ax+b}{x^2+1}\Leftrightarrow\left(x^2+1\right)P-\left(ax+b\right)=0\)
\(\Leftrightarrow Px^2-ax+P-b=0\left(1\right)\)
Vì giá trị nhỏ nhất và giá trị lớn nhất đều khác 0, nên \(P\ne0\)
Để P tồn tại thì phương trình (1) phải có nghiệm hay \(\Delta_{\left(1\right)}\ge0\)
\(\Leftrightarrow\left(-a\right)^2-4P\left(P-b\right)\ge0\Leftrightarrow4P^2-4Pb-a^2\le0\left(2\right)\)
Gọi \(P_1,P_2\left(P_1< P_2\right)\) là 2 nghiệm của phương trình \(4P^2-4Pb-a^2=0\left(3\right)\)
Khi đó phương trình (2) có nghiệm \(P_1\le P\le P_2\) nên P đạt Min tại giá trị \(P_1\), đạt Max tại giá trị \(P_2\).
Do đó, yêu cầu của bài toán chỉ thỏa mãn khi và chỉ khi phương trình (3) có 2 nghiệm -1 và 4, tức: \(\left\{{}\begin{matrix}4+4b-a^2=0\\64-16b-a^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=3\\a^2=16\end{matrix}\right.\) hay \(\left\{{}\begin{matrix}b=3\\a=\pm4\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}a=4\\b=3\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}a=-4\\b=3\end{matrix}\right.\)

So sánh phân số bằng cách quy đồng mẫu số
\(\dfrac{6}{17}\) < \(\dfrac{x}{22}\) < \(\dfrac{7}{17}\)
\(\dfrac{6\times22}{17\times22}\) < \(\dfrac{x\times17}{22\times17}\)< \(\dfrac{7\times22}{17\times22}\)
132 < \(x\times\) 17 < 154
132 : 17 < \(x\) < 154 : 17
\(\dfrac{132}{17}\) < \(x\) < \(\dfrac{154}{17}\)
7,76 < \(x\) < 9,05
Vì \(x\) là số tự nhiên nên \(x\) = 8
Vậy số cần điền vào chỗ trống là 8
Đáp số: 8
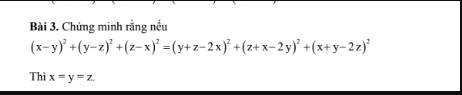
Uả rồi đề kiểu thế thì ai làm đc hả bà?