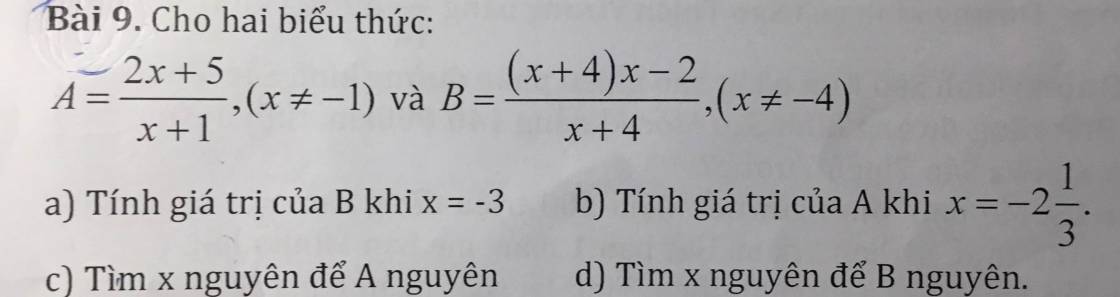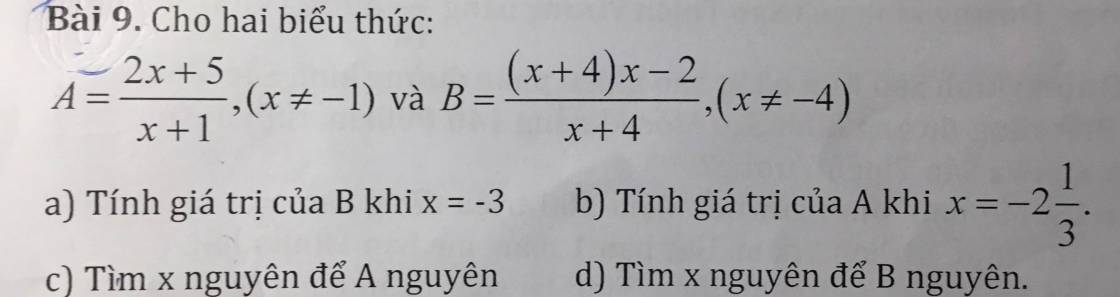cho tam giác ABC vuông tại A,AH vuông với BC,phân giác AD của tam giác ABC,phân giác HM,HN của tam giác HAB,HAC.Cmr:a,DM//AC b,AD=MN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



A = \(\sqrt{3+2\sqrt{2}}\) - \(\sqrt{\dfrac{\sqrt{2}-1}{\sqrt{2}+1}}\)
A = \(\sqrt{2+2\sqrt{2}+1}\) - \(\sqrt{\dfrac{\left(\sqrt{2}-1\right)\left(\sqrt{2}-1\right)}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}}\)
A = \(\sqrt{\left(\sqrt{2}+1\right)^2}\) - \(\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{2-1}}\)
A = \(\sqrt{2}\) + 1 - \(\sqrt{2}\) + 1
A = 2
A = \(\dfrac{2+\sqrt{3}}{\sqrt{7-4\sqrt{3}}}\) - \(\dfrac{2-\sqrt{3}}{\sqrt{7+4\sqrt{3}}}\)
A = \(\dfrac{2+\sqrt{3}}{\sqrt{4-4\sqrt{3}+3}}\) - \(\dfrac{2-\sqrt{3}}{\sqrt{4+4\sqrt{3}+3}}\)
A = \(\dfrac{2+\sqrt{3}}{\sqrt{\left(2-\sqrt{3}\right)^2}}\) - \(\dfrac{2-\sqrt{3}}{\sqrt{\left(2+\sqrt{3}\right)^2}}\)
A = \(\dfrac{2+\sqrt{3}}{2-\sqrt{3}}\) - \(\dfrac{2-\sqrt{3}}{2+\sqrt{3}}\)
A = \(\dfrac{\left(2+\sqrt{3}\right)^2-\left(2-\sqrt{3}\right)^2}{\left(2-\sqrt{3}\right).\left(2+\sqrt{3}\right)}\)
A = \(\dfrac{\left(2+\sqrt{3}-2+\sqrt{3}\right)\left(2+\sqrt{3}+2-\sqrt{3}\right)}{4-3}\)
A = \(\dfrac{2\sqrt{3}.4}{1}\)
A = 8\(\sqrt{3}\)

c, A = \(\dfrac{2x+5}{x+1}\) (\(x\ne\) -1)
A \(\in\) Z ⇔ 2\(x\) + 5 ⋮ \(x\) + 1
2(\(x+1\)) + 3 ⋮ \(x\) + 1
3 ⋮ \(x\) + 1
\(x+1\) \(\in\)Ư(3) = { -3; -1; 1; 3}
\(x\) + 1 \(\in\) { -4; -2; 0; 2}
d, B = \(\dfrac{\left(x+4\right)x-2}{\left(x+4\right)}\) (\(x\ne\) -4)
B \(\in\) Z ⇔ (\(x+4\))\(x\) - 2 ⋮ \(x+4\)
2 ⋮ \(x+4\)
\(x+4\) \(\in\) Ư(2) = { -2; -1; 1; 2}
\(x\) \(\in\) { -6; -5; -3; -2}

\(a,B=\dfrac{\left(-3+4\right).\left(-3\right)-2}{-3+4}=\dfrac{-3-2}{1}=-5\\ d,A=\dfrac{2.\left(-2\dfrac{1}{3}\right)+5}{-2\dfrac{1}{3}+1}=\dfrac{2.\dfrac{-7}{3}+5}{-\dfrac{7}{3}+1}=\dfrac{-\dfrac{14}{3}+5}{-\dfrac{4}{3}}=\dfrac{\dfrac{1}{3}}{-\dfrac{4}{3}}=-\dfrac{1}{4}\)

\(P=\dfrac{2x\sqrt[]{x}-\sqrt[]{x}+1}{x-1}\left(x\ge0;x\ne1\right)\)
\(\Rightarrow P=\dfrac{x\sqrt[]{x}-\sqrt[]{x}+x\sqrt[]{x}+1}{x-1}\)
\(\Rightarrow P=\dfrac{\sqrt[]{x}\left(x-1\right)+\sqrt[]{x^3}+1}{x-1}\)
\(\Rightarrow P=\dfrac{\sqrt[]{x}\left(x-1\right)}{x-1}+\dfrac{\left(\sqrt[]{x}+1\right)\left(x-\sqrt[]{x}+1\right)}{\left(\sqrt[]{x}-1\right)\left(\sqrt[]{x}+1\right)}\)
\(\Rightarrow P=\sqrt[]{x}+\dfrac{\left(x-\sqrt[]{x}+1\right)}{\left(\sqrt[]{x}-1\right)}\)

\(2.\left(x-1\right).\left(2+x\right)=2.\left(x^2-x+2x-2\right)\\ =2.\left(x^2+x-2\right)\\ =2x^2+2x-4\)