tìm các số x,y thỏa mãn (x+1).y -x =14
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


15199 = 15199
15150 = 2.3.52.101
ƯCLN(15199; 15150) = 1

A = \(\dfrac{-8}{n-7}\)
Để A là phân số thì n \(\in\) Z; n ≠ 7

a) [(-18) + (-17)] : 5
= -35 : 5
= -7
b) 666 - (-422) - 100 - 88
= 666 + 422 - 188
= 1088 - 188
= 900
c) (30 - 20).(-2).2 - 6.(-7 - 3)
= 10.(-4) - 6.(-10)
= 10.(-4 + 6)
= 10.2
= 20
d) 105 - 301 + (-129) - (-255)
= (105 + 255) - (301 + 129)
= 360 - 430
= -70


\(\dfrac{17}{25}\cdot\dfrac{10}{13}+\dfrac{17}{25}+\dfrac{3}{13}+\dfrac{8}{25}\)
\(=\dfrac{170}{325}+\dfrac{17}{25}+\dfrac{3}{13}+\dfrac{8}{25}\)
\(=\dfrac{34}{65}+\left(\dfrac{17}{25}+\dfrac{8}{25}\right)+\dfrac{3}{13}\)
\(=\dfrac{34}{65}+\dfrac{25}{25}+\dfrac{3}{13}\)
\(=\dfrac{34}{65}+\dfrac{1}{1}+\dfrac{3}{13}\)
\(=\dfrac{34}{65}+\dfrac{65}{65}+\dfrac{3}{13}\)
\(=\dfrac{99}{65}+\dfrac{15}{65}\)
\(=\dfrac{114}{65}\)

Số học sinh lớp 6A
\(120\cdot\dfrac{1}{2}=60\left(hs\right)\)
Từ bài toán, ta có sơ đồ:
Tổng: 60
Lớp 6B: |------------------------------------|
| 6 học sinh
Lớp 6C: |--------------------------------------------|
Lớp 6C có số học sinh là:
$\left(60+6\right):2=33 \left(\text{học sinh}\right)$
Lớp 6B có số học sinh là:
$60-33=27\left(\text{học sinh}\right)$
Đáp số: Lớp 6A: $60\text{học sinh}$
Lớp 6C: $33\text{học sinh}$
Lớp 6B: $27\text{học sinh}$

2; (\(x;y\)) = ? Biết \(\dfrac{x}{3}\) - \(\dfrac{1}{y+1}\) = \(\dfrac{1}{6}\) (đk \(x;y\) \(\in\) Z; y ≠ - 1)
\(\dfrac{x}{3}\) = \(\dfrac{1}{6}\) + \(\dfrac{1}{y+1}\)
\(\dfrac{x}{3}\) .6 = (\(\dfrac{1}{6}\) + \(\dfrac{1}{y+1}\)).6
2\(x\) = 1 + \(\dfrac{6}{y+1}\)
\(x\in\) Z ⇔ 6 ⋮ y + 1
y + 1 \(\in\) Ư(6) = {-6; -3; -2; -1; 1; 2; 3; 6}
Lập bảng ta có:
| y + 1 | -6 | -3 | -2 | -1 | 1 | 2 | 3 | 6 |
| y | -7 | -4 | -3 | -2 | 0 | `1 | 2 | 4 |
| \(x\) = (1 + \(\dfrac{6}{y+1}\)).\(\dfrac{1}{2}\) | 0 | - \(\dfrac{1}{2}\) | -1 | - \(\dfrac{5}{2}\) | \(\dfrac{7}{2}\) | 2 | \(\dfrac{3}{2}\) | \(\dfrac{11}{10}\) |
| loại | loại | loại | loại | loại |
Theo bảng trên ta có các cặp \(x;y\) nguyên thỏa mãn đề bài là:
(\(x;y\)) = (0; -7); (-1; -3); (2; 1);

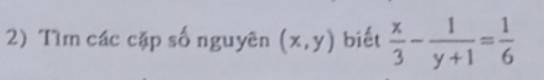
(x+1).y- x=14
(x+1).y- x-1 = 14-1
(x+1).y - (x+1) = 13
(x+1).(y-1) = 13
=> (x+1) và (y-1) E Ư(13) = { 1;-1;13;-13}
Ta có bảng:
x + 1 1 -1 13 -13
y - 1 13 -13 1 -1
x 0 -2 12 -14
y 14 -12 2 0
Vậy (x,y) E ......