a, Diện tích của tam giác ABC là: 9\(\times\)12: 2= 54 (cm²)

b, HC = AC - AH = AC - \(\dfrac{1}{4}\)AC= \(\dfrac{3}{4}\)AC

    S_FHC = \(\dfrac{3}{4}\)S_ACF (vì hai tam giác có chung chiều cao hạ từ đỉnh F xuống đáy AC và HC = \(\dfrac{3}{4}\)AC)

       Độ dài AF bằng: \(\dfrac{1}{3-1}\)BF =  \(\dfrac{1}{2}\)BF

     S_ACF = \(\dfrac{1}{2}\) S_FBC ( vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AF và  AF = \(\dfrac{1}{2}\)BF)

Tỉ số diện tích của tam giác FHC và diện tich tam giác FBC là:

                \(\dfrac{3}{4}\) \(\times\) \(\dfrac{1}{2}\) = \(\dfrac{3}{8}\)

Đáp số: a, 54 cm²

              b, \(\dfrac{3}{8}\)

\(x+6⋮x-1\)

Ta có: \(x-1+7\)

Mà: \(x-1⋮x-1\)

=> \(7⋮x-1\)

\(\Rightarrow x-1\inƯ\left(7\right)\)

\(Ư\left(7\right)=\left\{1;-1;7;-7\right\}\)

Th1: \(x-1=1\Rightarrow x=2\)

Th2: \(x-1=-1\Rightarrow x=0\)

Th3: \(x-1=7\Rightarrow x=8\)

Th4: \(x-1=-7\Rightarrow x=-6\)

Vậy: \(x\in\left\{2;0;8;6\right\}\) thì \(x+6⋮x-1\)

\(x+6\)⋮\(x-1\)

\(x-1+7\) ⋮ \(x-1\)

             7⋮ \(x-1\)

Ư(7) = {-7;  -1; 1; 7}

Lập bảng ta có: 

Theo bảng trên ta có:

Các giá trị của \(x\) thỏa mãn đề bài lần lượt là: -6; 0; 2; 8

Vậy \(x\) \(\in\) {-6; 0; 2; 8}

1.
a) \(3^4\times3^5\times3^6=3^{4+5+6}=3^{15}\)

b) \(5^2\times5^4\times5^5\times25=5^2\times5^4\times5^5\times5^2=5^{2+4+5+2}=5^{13}\)

c) \(10^8\div10^3=10^{8-3}=10^5\)

d) \(a^7\div a^2=a^{7-2}=a^5\)

2.

\(987=900+80+7\\ =9\times100+8\times10+7\\ =9\times10^2+8\times10^1+7\times10^0\)

\(2021=2000+20+1\\ =2\times1000+2\times10+1\times1\\ =2\times10^3+2\times10^1+1\times10^0\)

\(abcde=a\times10000+b\times1000+c\times100+d\times10+e\times1\\ =a\times10^4+b\times10^3+c\times10^2+d\times10^1+e\times10^0\)

Lần sau chú ý đăng đúng môn học nha.

\(a,3^4.3^5.3^6=3^{\left(4+5+6\right)}=3^{15}\)

\(b,5^2.5^4.5^5.25=5^2.5^4.5^5.5^2=5^{\left(2+4+5+2\right)}=5^{13}\)
\(c,10^8:10^3=10^8.\dfrac{1}{10^3}=10^5\)

\(d,a^7:a^2=a^7.\dfrac{1}{a^2}=\dfrac{a^7}{a^2}=a^5\)

a) 3⁴⁺⁵⁺⁶ = 3¹⁵ 

b) ( 25 = 5² ) 5^2+4+5+2 = 5¹³

c) 10^8-3 = 10⁵

d) a^7-2 = a⁵

S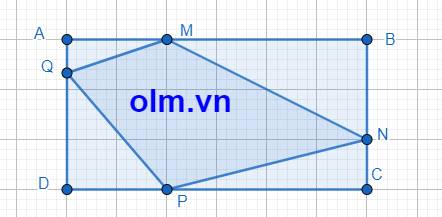

AQ = DA - DQ = DA - \(\dfrac{3}{4}\)DA = \(\dfrac{1}{4}\)DA

S_AMQ = \(\dfrac{1}{4}\)S_AMD (vì hai tam giác có chung chiều cao hạ từ đỉnh M xuống đáy AD và AQ = \(\dfrac{1}{4}\)AD)

S_AMD = \(\dfrac{1}{3}\)S_ABD ( vì hai tam giác có chung chiều cao hạ từ đỉnh D xuống đáy AB và AM = \(\dfrac{1}{3}\)AB)

S_ABD =  \(\dfrac{1}{2}\)S_ABCD(vì ABCD là hình chữ nhật)

S_AMQ = \(\dfrac{1}{4}\times\dfrac{1}{3}\times\dfrac{1}{2}\)S_ABCD = 216\(\times\) \(\dfrac{1}{24}\) = 9 (cm²)

S_MBN  = \(\dfrac{2}{3}\)S_BCM (vì hai tam giác có chung chiều cao hạ từ đỉnh M xuống đáy BC và BN = \(\dfrac{2}{3}\)BC)

BM = AB - AM = AB - \(\dfrac{1}{3}\)AB = \(\dfrac{2}{3}\)AB

S_BCM  = \(\dfrac{2}{3}\)S_ABC (vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AB và BM = \(\dfrac{2}{3}\)AB)

S_ABC = \(\dfrac{1}{2}\)S_ABCD (vì ABCD là hình chữ nhật)

S_MBN = \(\dfrac{2}{3}\times\dfrac{2}{3}\times\dfrac{1}{2}\)S_ABCD = 216\(\times\)\(\dfrac{2}{9}\) = 48 (cm²)

CN = BC - BN = BC - \(\dfrac{2}{3}\)BC = \(\dfrac{1}{3}\)BC 

S_CPN = \(\dfrac{1}{3}\)S_PBC (vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy BC và CN = \(\dfrac{1}{3}\)BC)

S_PBC  = \(\dfrac{2}{3}\)S_BCD (vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy CD và CP = \(\dfrac{2}{3}\)CD)

S_BCD = \(\dfrac{1}{2}\)S_ABCD (vì ABCD là hình chữ nhật)

S_CPN = \(\dfrac{1}{3}\times\dfrac{2}{3}\times\dfrac{1}{2}\)S_ABCD =  216 \(\times\) \(\dfrac{1}{9}\) = 24 (cm²)

S_DPQ  = \(\dfrac{3}{4}\)S_DPA (vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy DA và DQ = \(\dfrac{3}{4}\)DA)

DP = CP - DC = DC - \(\dfrac{2}{3}\)DC = \(\dfrac{1}{3}\)DC 

S_DPA = \(\dfrac{1}{3}\)S_ACD(vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy CD và DP = \(\dfrac{1}{3}\)DC)

S_ACD = \(\dfrac{1}{2}\)S_ABCD(vì ABCD là hình chữ nhật) 

S_DPQ = \(\dfrac{3}{4}\times\dfrac{1}{3}\times\dfrac{1}{2}\) S_ABCD = 216 \(\times\) \(\dfrac{1}{8}\) = 27 (cm²)

S_MNPQ = 216 - (9+ 48 + 24 + 27) = 108(cm²)

Đáp số: 108 cm²

  a,

S  =     1 -  3 + 3² - 3³+...+3⁹⁸ - 3⁹⁹

S  =   3⁰ - 3¹ + 3² - 3³+...+ 3⁹⁸ - 3⁹⁹

xét dãy số: 0; 1; 2; 3;...;99 

Dãy số trên là dãy số cách đều với khoảng cách là: 1 - 0 = 1

Dãy số trên có số số hạng là: (99 - 0): 1 + 1 = 100 (số)

100 : 4 = 25

Vậy ta nhóm 4 số hạng liên tiếp của tổng S thành 1 nhóm thì: 

S = ( 1 - 3 + 3² - 3³) +....+( 3⁹⁶ - 3⁹⁷ + 3⁹⁸ - 3⁹⁹)

S = - 20+...+ 3⁹⁶.(1 - 3 + 3² - 3³)

S = - 20 +...+ 3⁹⁶.(-20)

S = -20.( 3⁰ + ...+ 3⁹⁶) (đpcm)

b,

  S           = 1 - 3 + 3² - 3³+...+ 3⁹⁸ - 3⁹⁹

3S          =      3  - 3² + 3³-...-3⁹⁸  + 3⁹⁹ - 3¹⁰⁰

3S + S   =    - 3¹⁰⁰ + 1

4S        = - 3¹⁰⁰ + 1 

 S        = ( -3¹⁰⁰ + 1): 4

S        = - ( 3¹⁰⁰ - 1) : 4

Vì S là số nguyên nên 3¹⁰⁰ - 1 ⋮ 4 ⇒ 3¹⁰⁰ : 4 dư 1 (đpcm)

nhớ ngắn gọn nha

D={x/x*4+1;x ϵ N; x < 5}

D = {\(x\) = 4k +1/k\(\in\)N; k ≤ 4}

C={x/ x . 10 / x ϵ N*; x<10}

C = {\(x\)  = 10\(k\)/\(k\) \(\in\)N^*; \(k\le\)9}

\(\dfrac{4}{9}-x=\dfrac{1}{8}\\ x=\dfrac{4}{9}-\dfrac{1}{8}=\dfrac{32}{72}-\dfrac{9}{72}\\ x=\dfrac{23}{72}\)

\(\dfrac{4}{9}-x=\dfrac{1}{8}\)

`\Rightarrow`\(x=\dfrac{4}{9}-\dfrac{1}{8}\)

`\Rightarrow`\(x=\dfrac{23}{72}\)